20 Polygons
We’ve made great progress on understanding the sphere: we’ve discovered the geodesics, found enough isometries to do meaningful work (we can move any point to any other, and any geodesic to any other), analyzed circles and defined both acceleration and curvature. With these tools in hand we are ready to confront some of the most surprising differences between the geometry of the sphere and that of the plane, which are become visible when studying polygons.
An \(n\)-gon is a polygon with n vertices (or equivalently, with \(n\) edges). In the plane we studied \(3-\)gons (triangles), 4-gons (quadrilaterals), and beyond, but we never mentioned 2-sided shapes. Why? Well 2-gons (or bigons, if you are feeling fancy) do not exist in \(\EE^2\)!
This is because for a two sided shape to exist, its two sides would have to meet each other twice (once at each vertex). And we proved that Euclidean lines are given by affine equations, and such curves can only intersect once, lest they be equal (linear algebra!).
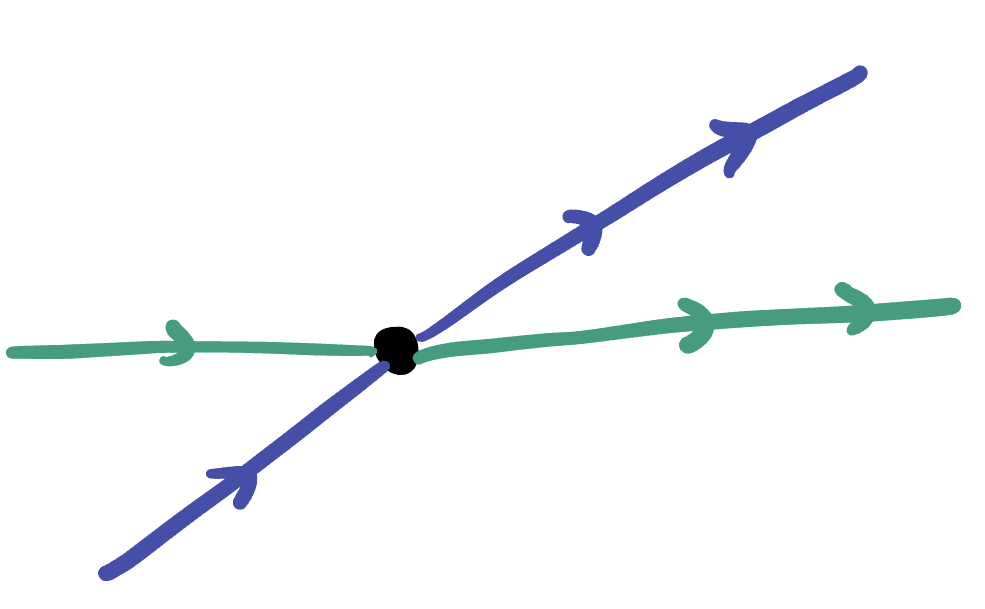
However, this basic behavior of lines is very different on the sphere.
Theorem 20.1 (Geodesics intersect twice) Any two distinct geodesics on \(\SS^2\) intersect exactly twice.
Proof. Let \(C_1\) and \(C_2\) be two geodesics on \(\SS^2\). Each is a great circle, and so is described by a plane passing through the origin. But two planes passing through the origin of \(\EE^3\) must intersect each other in a line! Thus, these two planes have an entire line through the origin in common, and this line must intersect the sphere in two points. These two points are then intersections between \(C_1\) and \(C_2\).
There cannot be any more intersections, as we can see also by thinking about the linear algebra of planes in \(\EE^3\): if our curves had three points of intersection on the sphere, at least one of them would not be a multiple of the others (as the only multiple of a point \(p\) which still lies on \(\SS^2\) is \(-p\)). Thus, we have three non-collinear points which lie on both geodesics. But, three points in \(\EE^3\) fully determine a plane, so if these points lie on both planes, the planes are equal, and so the geodesics themselves are equal (thus not distinct).
Recall the definition of parallel - we said that two lines were parallel if they did not intersect! But all lines on \(\SS^2\) intersect: thus there are no parallel lines at all!
Corollary 20.1 There are no parallel lines on the sphere. Thus, Playfair’s axiom is false for \(\SS^2\).
Playfairs axiom (which stated that given any line, and any point not on that line) is equivalent to Euclid’s 5th postulate, assuming the first four. We do not have this equivalence available to us here (because not all of the first four are true in spherical geometry!) so we have to separately ask about the\(5^{th}\):
Exercise 20.1 (Euclid’s Fifth Postulate is False on \(\SS^2\)) Show that Euclids postulate is false by finding a counterexample: give two geodesics on the sphere that intersect a third in angles which sum to \(\pi\), but nonetheless intersect.
Remark 20.1. Its actually hard to precisely make sense of Euclid’s postulate on the sphere, in his original wording, as it talks about finding an intersection on one side of the crossing line or the other. But on the sphere there are no sides: everything meets up on the back!
But besides answering these interesting foundational questions, realizing that pairs of geodesics intersect each other twice has another important corollary:
Corollary 20.2 (Bigons Exist) Bigons exist in spherical geometry.
Thus, we begin our study of polygons not with triangles as we did in Euclidean space, but at an even lower, more basic level: we begin with bigons!
20.1 Bigons
A bigon has two angles, and two sides. At first, we know nothing else about them, so we might give a different name to each side and to each angle, like so:
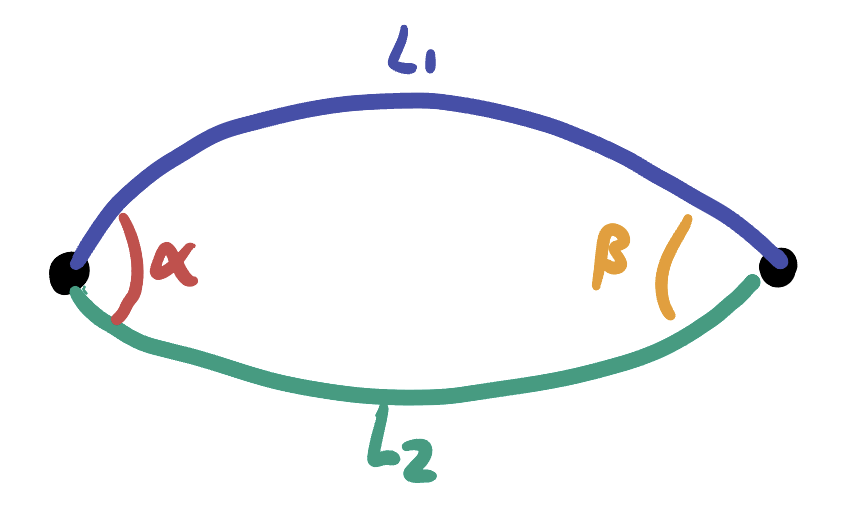
Just like in trigonometry, our goal here is to try to discover relations between the sides and angles of a bigon. However, unlike trigonometry - the relations here turn out to be very simple: there just aren’t many ways to make a bigon!
Proposition 20.1 Both sides of a bigon have length \(\pi\):
Proof. We saw in Theorem 20.1 that if one vertex of a bigon is \(p\), then its sides, being geodesics, meet again at the point antipodal to \(p\). Thus, each side of the bigon is exactly half of a great circle, and so has length \(\frac{1}{2}2\pi =\pi\).
Next, we should ask about the bigon’s angles: is it possible to have a bigon with two angles of different measures?
Proposition 20.2 The two angles of a bigon are equal to one another.
Proof. To make things easier to picture, we can use an isometry to move one of the vertices of our bigon to the north pole (and thus the other to the south pole, since they are antipodal).
Now, the sides of the bigon make a right angle with the equator (since they are great circles going from the north to south pole) and so reflection in the equator sends the bigon to itself, exchanging its two vertices.
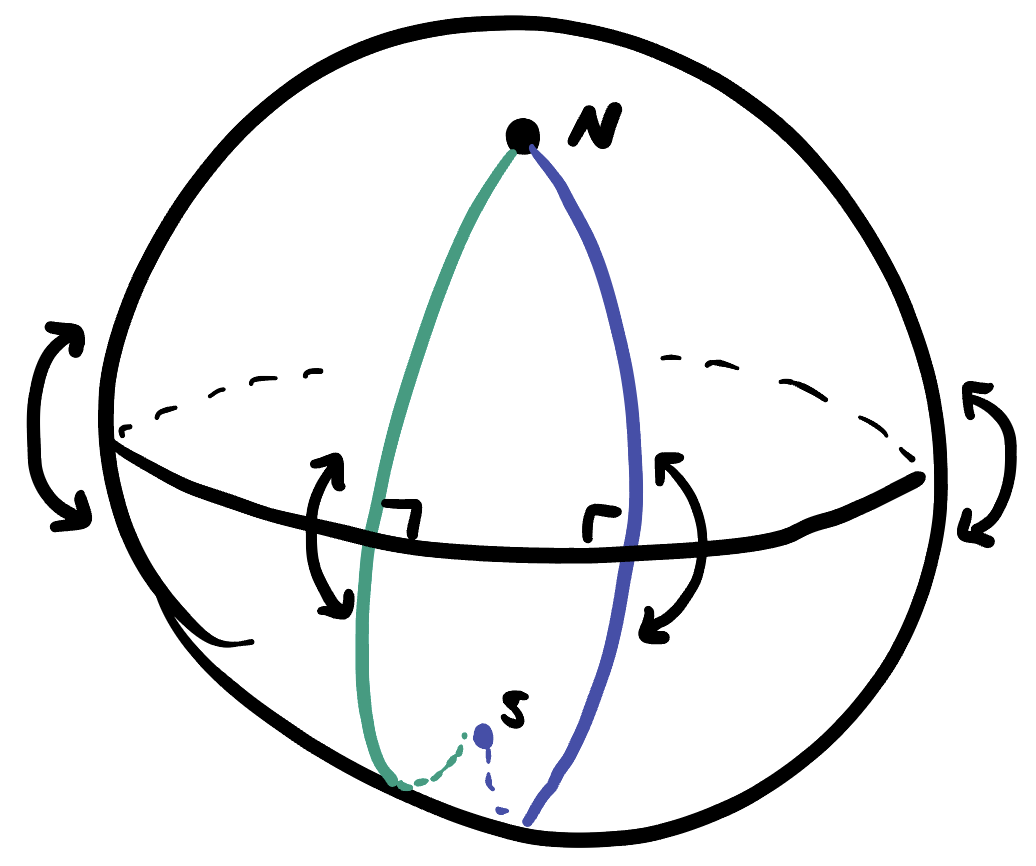
But now we are done! Isometries preserve angle, and so if there’s an isometry that swaps the vertices of the bigon they must have the same angle.
Thus bigons only have one free parameter: once you know the angle a bigon has at one vertex, you know everything there is to know to construct the entire bigon.
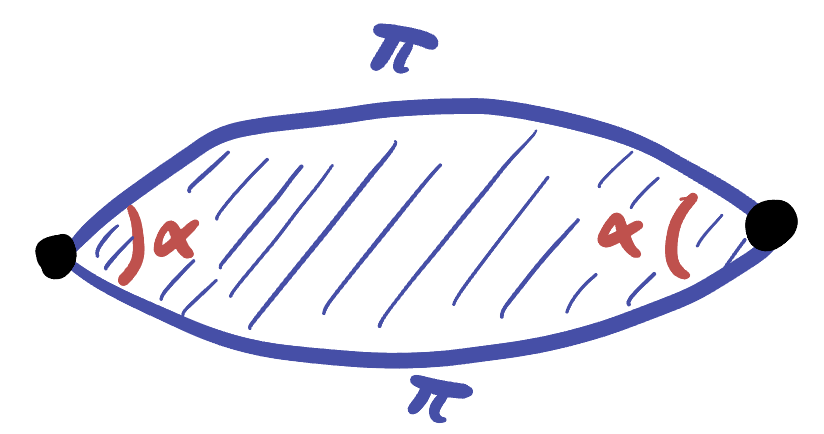
Indeed - up to isometry there is exactly one bigon for every angle \(\theta\in(0,2\pi)\), where the bigon with angle \(\pi\) is exactly one hemisphere of the sphere, and a bigon with angle \(>\pi\) covers more than half the sphere. Strange world spherical geometry is, where a polygon can have only two sides and take up more than half of the universe!
The final geometric quantity we may wish to understand is the area of a bigon.
20.2 Triangles
Having discovered literally everything there is to know about bigons, its time to move on to the world of triangles. First, we should be careful and check that triangles even exist! This might sound silly - but our recent experience with bigons should warn us to be extra careful.
Proposition 20.3 (Spherical Triangles Exist) Any three points not all lying on the same great circle determine a triangle.
Proof. Let \(p\) \(q\) and \(r\) be any three points on \(\SS^2\) not on the same great circle. Draw the shorter geodesic segment connecting \(p\) and \(q\) (recall, there are two of these, as \(p\) and \(q\) both lie on a great circle: if \(p\) and \(q\) are antipodes then choose either segment).
Likewise, draw the shorter segments connecting \(p\) to \(r\) and \(q\) to \(r\). All we need to do to show this forms a triangle is to argue that these two new segments do not cross the first segment.
Of course, they do intersect the first segment at its endpoints \(p\) and \(q\)! But they can’t intersect it anywhere else - the entire great circles they define intersect the great circle containing \(p\) and \(q\) only at these points, and then at their antipodes \(-p\) and \(-q\).
But, since the segment connecting \(p\) and \(q\) was the shorter of the two geodesic segments, its not long enough to include both \(p\) as one of its endpoints, and \(-p\) as a point in the interior: then it would stretch more than half way around the sphere! Thus, these other intersections are not on the segment, and the three segments meet only at their vertices, forming a triangle.
Remark 20.2. Think for a moment from the perspective of an inhabitant of spherical geometry, who are so accustomed to dealing with bigons that when they start trying to understand Euclidean geometry, they don’t think twice and just immediately start their theory by investigating bigons. Whatever theorems they prove would be useless because they all implicitly are of the form the existence of bigons implies XXX and the premise is false: bigons do not in fact exist at all!
Now that we are confident in their existence, we turn to the most surprising - and at the same time the most useful - property of spherical triangles: their area is intimately tied to their angle sum.
Theorem 20.2 (Area of a Spherical Triangle) The area of a spherical triangle is equal to the angle sum, minus \(\pi\). In symbols, if a triangle \(T\) has angles of measure \(\alpha,\beta\) and \(\gamma\), then \[\mathrm{area}(T)=\alpha+\beta+\gamma-\pi\]
The style of proof here is quite clever, and uses our work with bigons! Indeed, we will cover the sphere with six bigons starting from our triangle, and find the triangle’s area by counting area overlaps.
Proof.
Exercise 20.2 What is the analogous formula for the area of a triangle on the sphere of curvature \(\kappa\)?
Hint: recall that the map taking the unit sphere to the sphere of radius \(R\) is a similarity of \(\EE^3\), and use what we know about similarities effect on area and angles to deduce this directly from the unit sphere case, without repeating the proof given in class.
This formula has some immediate and surprising consequences. Since polygons have nonzero (and positive!) area, we can use as a powerful tool in proving the nonexistence of various objects on the sphere. The strategy goes:
- Assume for contradiction a certain object exists
- break it into triangles
- compute the area of the shape, using these triangles
- find the area is zero or negative: contradiction!
- Thus, the object does not exist.
20.3 Quadrilaterals
Theorem 20.3 (Area of Spherical Quadrilaterals) The area of a convex spherical quadrilateral is equal to its angle sum minus \(2\pi\).
Proof. Let \(Q\) be a quadrilateral on \(\SS^2\), with angles \(\alpha,\beta,\gamma,\delta\). Choose two opposite vertices of \(Q\), and draw the line segment connecting them. This segment lies fully inside the quadrilateral (by convexity), and divides it into two triangles \(T_1\) and \(T_2\), dividing the angles \(\alpha=\alpha_1+\alpha_2\) and \(\gamma=\gamma_1+\gamma_2\) between them:
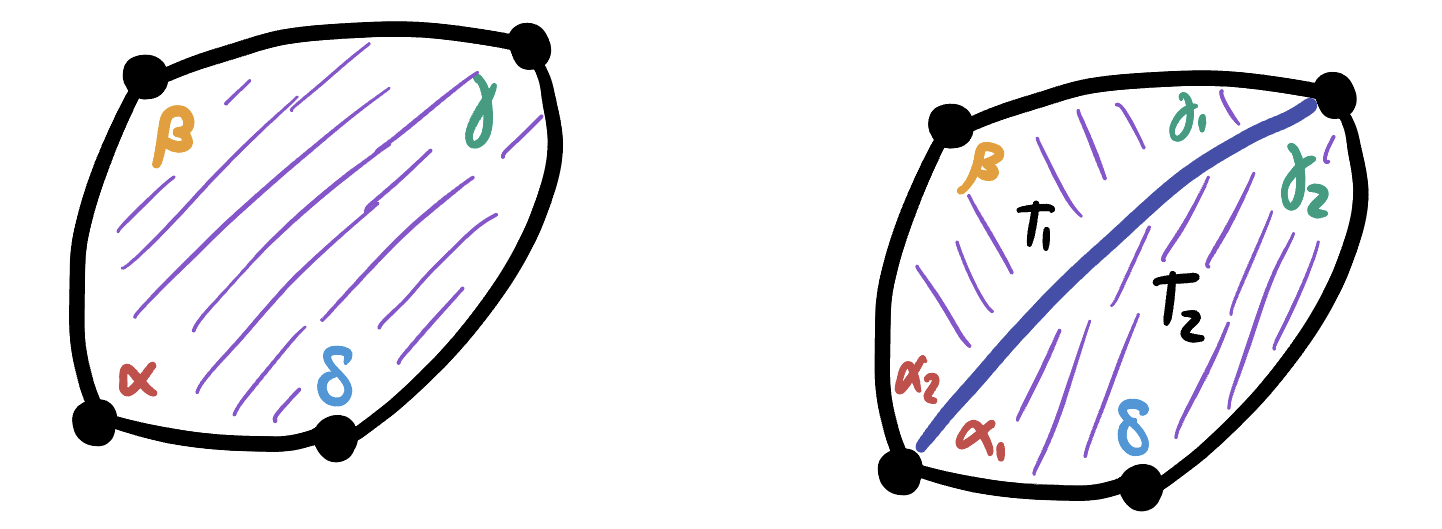
Now we can compute the area as the sum of the area of the triangles:
\[\begin{align*}\area(Q)&=\area(T_1)+\area(T_2)\\ &= (\alpha_1+\beta+\gamma_1-\pi)+(\gamma_2+\delta+\alpha_2-\pi)\\ &=(\alpha_1+\alpha_2)+\beta+(\gamma_1+\gamma_2)+\delta-2\pi\\ &=\alpha+\beta+\gamma+\delta-2\pi \end{align*}\]
This has some immediate surprising consequences, including the nonexistence of rectangles!
Corollary 20.3 (Rectangles do not exist.)
Proof. Assume that there is a quadrilateral \(R\) on \(\SS^2\) with four right angles. Then by the above, we can compute the area
\[\area(R)=\left(\frac\pi 2+\frac\pi 2+\frac\pi 2+\frac\pi 2\right)-2\pi = 0\]
But this is impossible, quadrilaterals cannot have zero area! Thus, we must have been wrong, and a right angled quadrilateral cannot in fact exist.
Exercise 20.3 What is the analogous formula for the area of a quadrilateral on a sphere of curvature \(\kappa\)?
20.4 Platonic Solids
Besides proving nonexistence results like that for rectangles, the triangle area formula helps us determine what regular polygons can be used to tile the sphere.
Recall we call a polygon regular if it has rotational symmetries about its center: in particular this implies that all its sides are the same length, and all its angles have the same measure (since isometries preserve both lengths and angles).
In the Euclidean plane, we know that regular polygons of all side numbers \(\geq 3\) exist (these are how Archimedes approximated the circle, after all!), but their angles are strictly determined by their number of sides. We proved in a previous homework that the angle sum of an \(n\)-gon is \((n-2)\pi\), and if all the angles of a regular \(n\) gon are equal, each angle must measure \(\theta_n = \frac{n-2}{n}\pi\).
This puts a strong restriction on which regular polygons can be used to tile the plane. To tile the plane, a necessary (but not sufficient) condition is that we need to be able to fit \(k\) copies of each polygon around a vertex, without any gaps or overalps. This tells us that the angles of a polygon that can tile must be \(\theta =\tfrac{2\pi}{k}\).
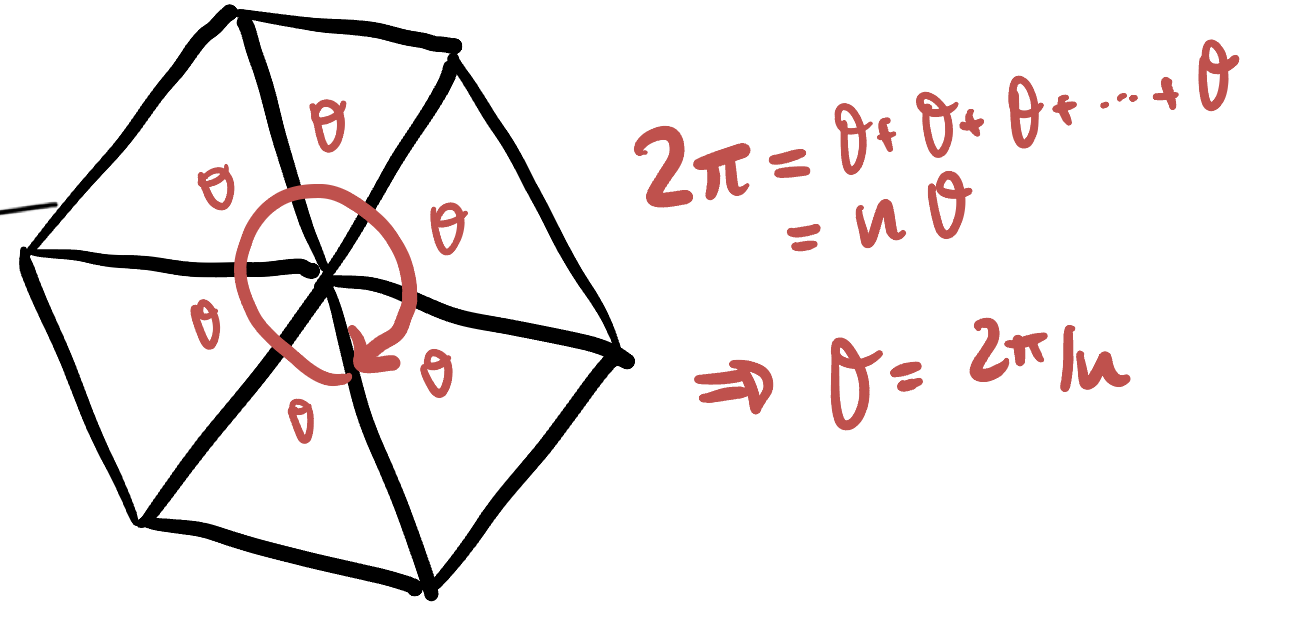
Thus, to figure out which polygons even have a chance of tiling the Euclidean plane, we want to know for which \(n\) (the number of sides) there the angle \(\theta_n\) is actually \(2\pi\) over an integer. We can start listing:
\[\theta_3=\frac{3-2}{3}{\pi}=\frac{\pi}{3}=\frac{2\pi}{6}\] \[\theta_4 = \frac{4-2}{4}\pi=\frac{\pi}{2}=\frac{2\pi}{4}\] \[\theta_5=\frac{5-2}{5}\pi=\frac{3\pi}{5}\] \[\theta_6=\frac{6-2}{6}{\pi}=\frac{2\pi}{3}\] \[\theta_7=\frac{7-2}{7}{\pi}=\frac{5\pi}{7}\]
Thus, we see that its possible to fit six triangles around a vertex, four squares around a vertex and three hexagons around a vertex, but as the angles \(\theta_5\) and \(\theta_7\) aren’t even divisions of \(2\pi\), there’s no nice way to fit pentagons or 7-gons around a vertex, and thus no hope of using them to tile the plane.
This is the start to the classification of regular tilings of the plane, where by what we see from the angle measures, its possible for triangles, squares and hexagons, but impossible for all other shapes!
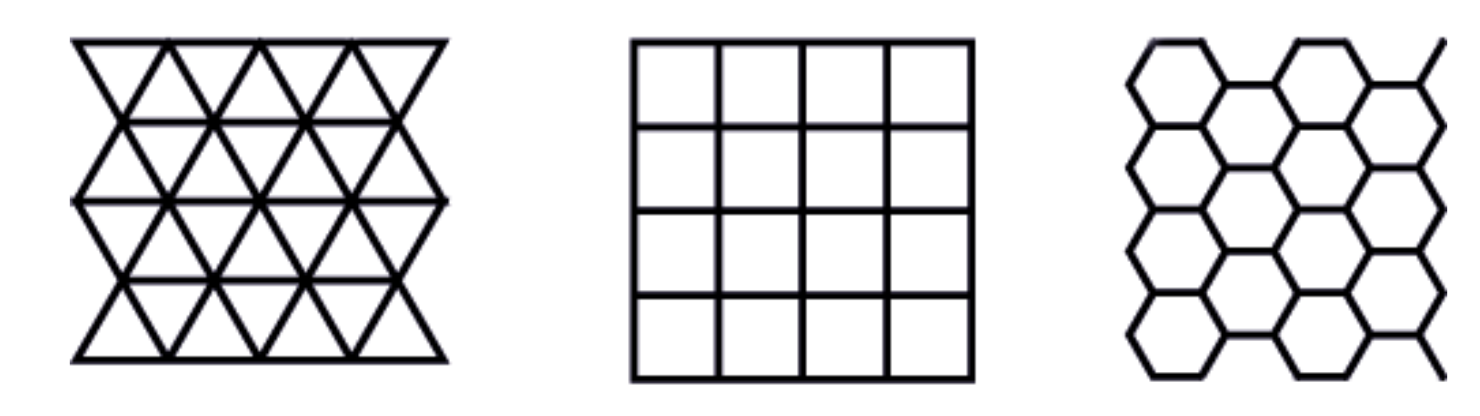
Our goal here is to investigate what changes on the sphere.
Exercise 20.4 (Spherical Pentagons)
Find a relationship between the area \(A\) of a spherical regular pentagon and its angle measure \(\alpha\). Hint: divide the spherical pentagon into five triangles
Show that there exists a spherical pentagon whose angle evenly divides \(2\pi\): how many of these spherical pentagons fit around a single vertex?
What is the area of such a spherical pentagon? How many of these pentagons does it take to cover the entire sphere?
The resulting tiling of the sphere is the dodecahedron - one of the Platonic solids discovered by the Greeks (though, usually these are imagined as having flat faces, instead of actually lying directly on the surface of the sphere). This is pretty encouraging, our simple investigation into areas of triangles led us all the way to the dodecahedron! But can it go farther? Can we learn exactly which polygons can tile the sphere from such meager data?
Exercise 20.5 (No Tiling by Hexagons) Show that there is no regular hexagon which can tile the sphere.
And, it only gets worse from here:
Exercise 20.6 Prove that for any \(n\geq 7\), there are no regular spherical \(n\) gons that can tile the sphere.
The problem we run into with hexagons is that their area must be zero, and its worth commenting briefly on what that means. Having zero area means the angle sum needed is equal to the Euclidean angle sum - and so this is just telling us that the sphere is the wrong spot to be looking for such a tiling; instead it exists in the Euclidean plane!
But what are we learning in the case of \(7\)-gons and above? If we try to find any value of \(k\) where the angles would be \(2\pi/k\), we get a negative area: this means the shapes both don’t exist on the sphere and don’t exist in Euclidean space. However, we will meet these tilings shortly, in hyperbolic space
So, we’ve found a pentagon that tiles \(\SS^2\), and no higher \(n\)-gons do. This leaves only three cases left to investigate: the bigons, triangles, and quadrilaterals!
For bigons, the condition that they tile the sphere is just that their angles are \(2\pi/n\): this is possible for every \(n\geq 2\), so we have an infinite collection of different bigon tilings:
But, these aren’t really that interesting: they’re just what you get by drawing an \(n\)-gon on the equator, and then extending perpendicular geodesics up to the north and south poles. Indeed, these are so simple that these tilings are often not even counted among the platonic solids!
The more interesting shapes appear when \(n=3\) and \(n=4\).
Exercise 20.7 Prove that there is exactly one quadrilateral that can tile the sphere. How many fit around each corner? How many quadrilaterals does it take to cover the sphere?
Which platonic solid does this correspond to?
Exercise 20.8 There are three different equilateral triangles that can be used to tile the sphere. Find them! For each triangle:
- How many fit around each vertex?
- How many are needed to cover the sphere?
- What platonic solid does this correspond to?
20.5 Trigonometry
We’ve already gotten an incredible amount of information out of just knowing how to relate angles to area of spherical triangles. But there is much more to be gained from studying the quantitative relationships between angles and lengths as well. This is the study of spherical trigonometry!
We will not dive too deeply into this material in this course, as it is a huge topic dating all the way back to the greeks, and navigation by the stars! Instead we aim to just give a taste.
As in Euclidean space, its easiest to start with as simple of triangles as possible. In \(\EE^2\) these were right triangles, as having a right angle makes a lot of things easier. In the sphere - we can do one better: well, really two better - there are triangles which have three right angles!
To see these exist - you can make one by starting with a right angle at the north pole, and following both geodesics down to the equator, then stopping and using the segment of the equator connecting the endpoints as the third side. The top angle was right by construction, and these next two are also right angles, as they are the intersection of the equator with geodesics through the north pole (as you showed on your last homework assignment).
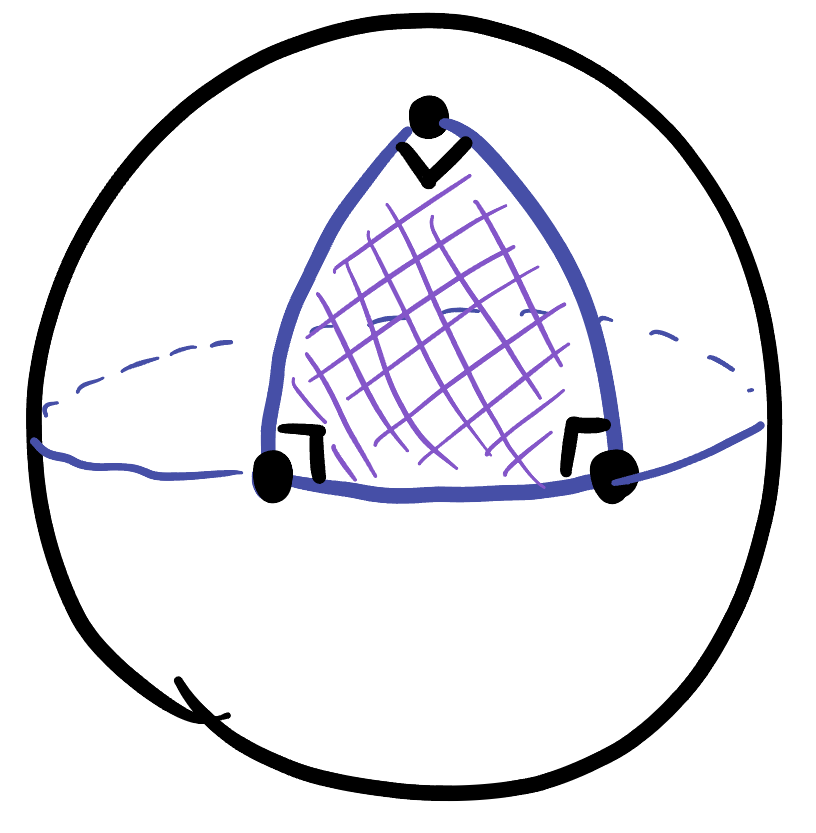
However, there is not a very interesting theory of the trigonometry of three-right angled triangles: it turns out that up to isometry, this example above is the only one.
Proposition 20.4 All triply right triangles on \(\SS^2\) are isometric to one another.
Proof.
Thus we completely understand these right triangles: they all have angles \(\pi/2\) (of course!), but they also have side lengths \(\pi/2\), and they have area $\(A=3\tfrac{\pi}{2}-\pi=\tfrac{\pi}{2}\): every geometric measurement here is equal to \(\pi/2\)!
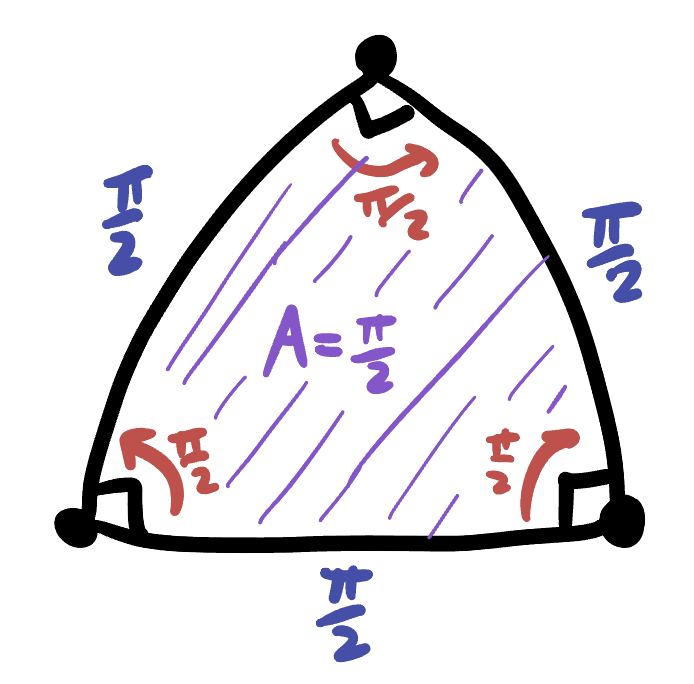
The next simplest case is that of doubly-right triangles. Let’s call the third angle of such a triangle \(\alpha\). These are also quite restricted: take the side opposite \(\alpha\) which contains the two right angles, and move it to a segment of the equator by isometries. Now, the other two sides are geodesics which make right angles with the equator: they intersect at the north pole! So, our triangle has two sides of length \(\pi/2\).
Now that we know this, the area is immediate: this is half of a bigon with angle \(\alpha\), so its area is \(\tfrac{1}{2}(2\alpha)=\alpha\). We can also quickly determine the third side length: the angle at \(N\) is \(\alpha\), and so the arclength along the equator (which is a unit circle) is also \(\alpha\).
20.5.1 Right Triangles
Things get both more interesting, and more complicated in the case of triangles with a single right angle. The fundamental trigonometric relationship for a right triangle is how the lenght of its hypotenuse depends on the lengths of its legs. In Euclidean space, this is the famous Pythagorean theroem, but in spherical geometry it takes on another form.
Theorem 20.4 (Spherical Pythagorean Theorem) Given a right triangle on \(\SS^2\) with side lengths \(a,b\) and hypotenuse \(c\), these three lengths satisfy the equation \[\cos(c)=\cos(a)\cos(b)\]
Exercise 20.9 (Deriving The Pythagorean Theorem) Prove that the formula given above really does hold for the legs and hypotenuse of a right triangle on \(\SS^2\), using the distance formula that we’ve already calculated:
\[\cos\dist(p,q)=p\cdot q\]
Hint: move your triangle so the right angle is at the north pole, and the legs are along the great circles on the \(xz\) and \(yz\) plane. Now you can write down exactly what the other two vertices are since you know they are distance \(a\) and \(b\) along these geodesics from \(N\)K
On a sphere of radius \(R\), a similar formula exists: here to be able to use arguments involving angles we need to divide all the distances by the sphere’s radius, but afterwards an argument analogous to the above exercise yields
\[\cos\left(\frac cR\right)=\cos\left(\frac aR\right)\cos\left(\frac bR\right)\]
Its often more useful to rewrite this result in terms of the curvature \(\kappa=1/R^2\)
Theorem 20.5 (Pythagorean Theroem of Curvature \(\kappa\)) On the sphere of curvature \(\kappa\), the two legs \(a,b\) and the hypotenuse \(c\) of a right triangle satisfy \[\cos\left(c\sqrt{\kappa}\right)=\cos\left(a\sqrt{\kappa}\right)\cos\left(b\sqrt{\kappa}\right)\]
As a sphere gets larger and larger in radius, it better approximates the Euclidean plane. We might even want to say something like in the limit \(R\to\infty\) (so, \(\kappa\to 0\)) the spherical geometry becomes euclidean. But how could we make such a statement precise? One way is to study what happens to the theorems of spherical geometry as \(\kappa\to 0\); and show that they become their Euclidean counterparts. The exercise below is our first encounter with this big idea:
Exercise 20.10 (Euclidean Geometry as the Limit of Shrinking Curvature) Consider a triangle with side lengths \(a,b,c\) in spherical geometry of curvature \(\kappa\). As \(\kappa\to 0\), the arguments of the cosines in the Pythagorean theorem become very small numbers, so it makes sense to approximate approximate these with the first terms of their Taylor series.
Compute the Taylor series of both sides of \[\cos\left(c\sqrt{\kappa}\right)=\cos\left(a\sqrt{\kappa}\right)\cos\left(b\sqrt{\kappa}\right)\]
in the limit \(\kappa\to 0\), we can ignore all but the first nontrivial terms. Show here that only keeping up to the quadratic terms on each side recovers the Euclidean Pythagorean theroem, \(c^2=a^2+b^2\).
Like in the plane, we might next hope to discover relationships between the sides of a spherical right triangle and its angle measures. And, indeed we can!
The corresponding laws of spherical trigonometry are as follows:
Theorem 20.6 (Spherical Trigonometric Relations) For a right triangle with angles \(\alpha,\beta\), corresponding opposite sides \(a,b\) and hypotenuse \(c\) the following relations hold:
\[\sin \alpha = \frac{\sin a}{\sin c}\hspace{1cm}\sin\beta =\frac{\sin b}{\sin c}\]
\[\cos\alpha = \frac{\tan b}{\tan c}\hspace{1cm}\cos\beta=\frac{\tan a}{\tan c}\]
Its instructive to compare these to their Euclidean counterparts: where the \(\sin\alpha = a/c\) and \(\cos\alpha = b/c\) for instance. The spherical versions have the same ratios, but the lengths are showing up inside trigonometric functions themselves!
These can be derived (though we will not, for the sake of time) using the geometry of planes in \(\EE^3\) - since great circles on the sphere are just intersections of planes through the origin with the sphere.
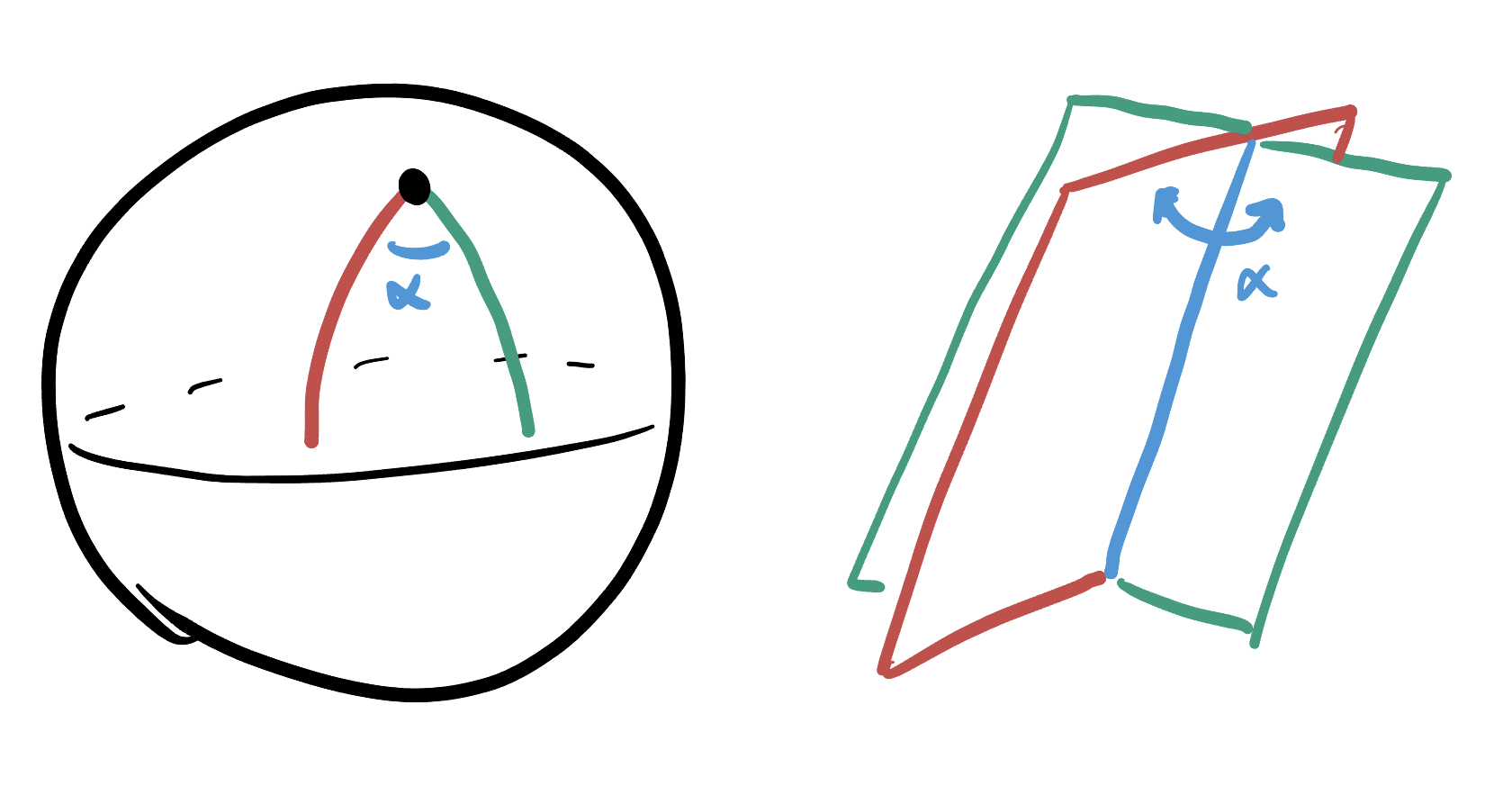
Here’s a nice derivation, which finds the angles between planes (and thus the angles between great circles) by finding the angles between their normal vectors.
One of the most biggest differences between spherical trigonometry and its Euclidean counterpart is that its possible to derive formulas for the length of a triangles’ sides in terms of only the angle information! This is impossible in Euclidean space because of the existence of similarities: there are plenty of pairs of triangles that have all the same angles but wildly different side lengths! No so in the geometry of the sphere.
Exercise 20.11 Using the trigonometric identities in Theorem 4 together with the spherical pythagorean theorem Theorem 2, show that the side length \(a\) of a right triangle can be computed knowing only the opposite angle \(\alpha\) and the adjacent angle \(\beta\) as
\[\cos a = \frac{\cos\alpha}{\sin\beta}\]
Hint: start with the formula for \(\cos\alpha\). Write out the tangents in terms of sines and cosines, then apply the pythagorean theorem to expand a term. Finally, use the definition of \(\sin\beta\) to regroup some terms.
Formulas such as this are incredibly useful for calculating the side lengths of polygons, by dividing them into triangles and using facts that are known about their angles.
Exercise 20.12 (Spherical Trigonometry) Use spherical trigonometry to figure out the side lengths of the pentagon you discovered in the first exercise.
Hint: can you further divide the five triangles you used before, into ten right triangles inside the pentagon?