3 Pythagoras
The pythagorean theorem needs no introduction, and is perhaps the most well known formula in mathematics from antiquity (and perhaps, only rivaled by \(E=mc^2\) in the modern era).
Theorem 3.1 On a right triangle with legs of length \(a,b\) and hypotenuse of length \(c\), these lengths satisfy \[a^2+b^2=c^2\]
This theorem is fundamental to almost all real-world applications of geometry because it is the Greek foundation for the distance function it lets us measure distance between two points in the plane if we only know their horizontal and vertical separations.
Pythagoras’ Theorem was not first discoverd by Pythagoras - and its first origins are lost to history though surviving tablets show that it was already in common use in Babylon by 3700 years ago.
The same theorem was discovered by many mathematicians the world over, from ancient india to china and the middle east. But it was the Greeks who, in building the Elements, first realized its essential reliance on the theory of parallels.
While we are these days accustomed to algebraic expressions occurring in the midst of geometric arguments (and so, think of the Pythagorean theorem primarily as an equation) the origin of this equation deals fundamentally with the area of squares. Indeed, Euclid’s original statement was:
In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.
And so, before we can proceed, we need to study area.
3.1 Areas
Just like measuring angles, Euclid needed some additional rules to specify how areas are to be measured. Here I’ve summarized these in a modern phrasing for us to use.
Definition 3.1 (Area Axioms)
- The area of a square of side length \(x\) is \(x^2\).
- Any two congruent shapes have the same area.
- If a shape \(R\) is the disjoint union of two shapes \(S\) and \(T\), the area of \(R\) is the sum of the areas of \(S\) and \(T\).
Proposition 3.1 (Area of a Rectangle) The area of a rectangle is equal to the product of its two side lengths.
Proof. Create a square of side lengths \(a+b\), and divide it up into a square with side lengths \(a\), one with side lengths \(b\) and two rectangles with sides \(a,b\), as shown in the following picture.
Let \(A_R\) denote the unknown area of the rectangle. Using the area axioms, we can write the area of the large square as a sum of the areas of its components \[(a+b)^2=a^2+b^2+2A_R\]
From here; its just algebra. Expanding the left hand side and cancelling like terms we find
\[A_R=ab\]
Exercise 3.1 Starting with segments of lengths \(a,b\) and using the postulates and what we have proven or stated in this text so far, construct the diagram used in the proof of Proposition 3.1, and justify it has the properties claimed of it (made of two squares and two rectangles of the correct dimensions).
We can now use this result to deduce the area of right triangles as well.
Proposition 3.2 (Area of a Right Triangle) The area of a right triangle is half the product of its two legs.
Proof. In the proof of ?prp-rect-opposite-sides (showing that the opposing sides of a rectangle are the same length) we saw that the diagonal divides a rectangle into two congruent triangles.
Call the area of the rectangle \(A_R\) and the area of each of these triangles \(A_{T_1}\) and \(A_{T_2}\). Since the triangles are congruent their areas are equal (Area Axiom 2), and since they together make up the entire rectangle, \(A_R=A_{T_1}+A_{T_2}\) (Area Axiom 3). Putting these together
\[A_R=A_{T_1}+A_{T_2}=2A_{T_1}\implies A_{T_1}=\frac{1}{2}A_R\]
Since we know \(A_R\) is the product of its two side lengths, and these are the legs of each triangle, we see that the area of the right triangle is half the product of its side lengths, as claimed.
And finally we can extend this back to general triangles, recovering the familiar formula from high school geometry, that a triangle’s area is given by \(A=\tfrac{1}{2}bh\)
Proposition 3.3 (Area of a Triangle) The area of a triangle is half the product of its base and its height.
Exercise 3.2 Prove Proposition 3.3.
Hint - consider two cases: does the top vertex of the triangle lie over the base, or does it not? In both cases, try to use what we know about right triangles to help.
3.2 Proving the Pythagorean Theorem
This theorem has been proved many times! Indeed, there is an entire textbook by Elisha Scott Loomis devoted to distinct proofs of the Pythagorean theorem, collecting 367 in all, and this website gives 119 distinct proofs for you to peruse.
Euclid even proved this proposition in two distinct ways in The Elements, first in Book I, Proposition 47 and much later, in Book 6, Proposition 31.
However, as with many things in mathematics - time brings new insights and clairty even to the oldest of problems. The styles of proof that I personally find most elegant are all rearrangement proofs: starting with one collection of shapes and moving the pieces around in a way that forces the truth of the theorem.
A particularly ingenious rearrangement proof was devised in the mid 800s CE by Thābit ibn Qurra (full name أبو الحسن ثابت بن قرة بن زهرون الحراني الصابئ), a polymath from Baghdad who made contributions to mathematics, astronomy and medicine.
Proof.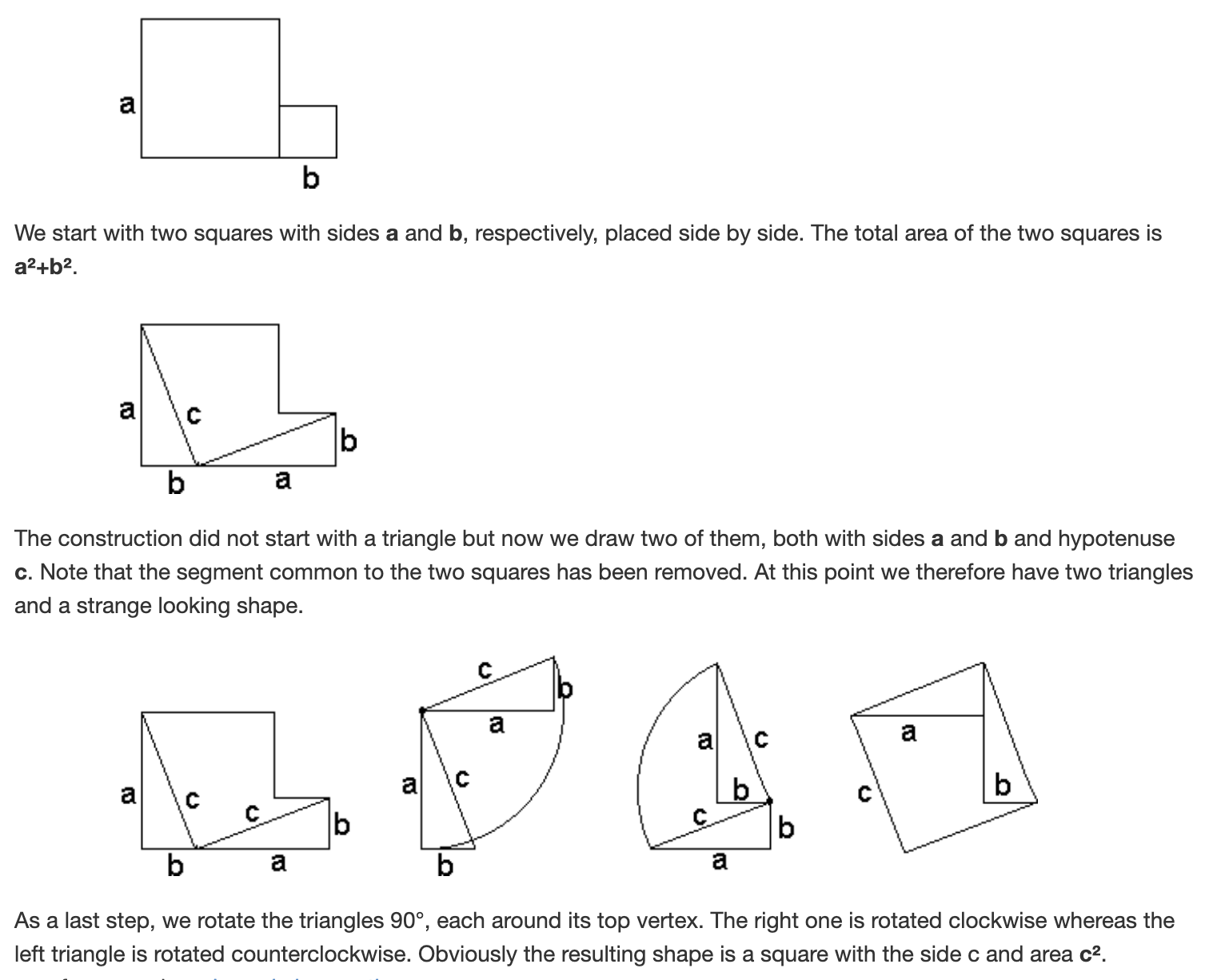 
Exercise 3.3 Justify that the resulting final shape here (in the proof by Qurra above) is indeed a square.
My favorite proof of the pythagorean theorem needs no words to be convincing: it’s core idea is contained in the following diagram.
Proof. The blue areas in these two pictures are the same, as all we have done is slide around the triangles.
Of course, to make this rigorous we have to explain why the re-arrangement really is the same square.
Variants of this proof were discovered by the 12th century Hindu mathematician Bhaskara (Bhaskara II), and even much earlier, appearing in the Chinese astronomical text Zhoubi Suanjing (周髀算經) from the second century BCE (and, claiming to record works from the 11th century BCE).
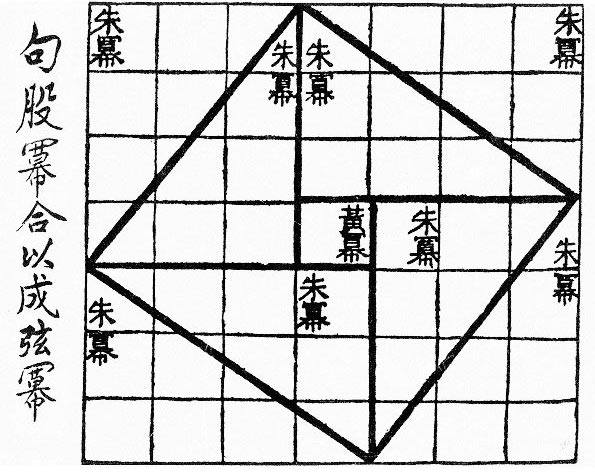
Exercise 3.4 Explain how the diagram from the Zhoubi Suanjing shows that \(a^2+b^2=c^2\) using the formulas we’ve derived for the areas of squares and right triangles, and some algebra.
3.3 The Irrationality of \(\sqrt{2}\)
Traditionally the realization that irrational numbers must exist is attributed to Pythagoras (or his followers, the Pythagoreans). While the usual story is likely apocryphal (where the Pythagoreans kept as a strict secret the existence of irrational numbers, and murdered Hippasus for divulging it), their discovery nonetheless revealed a tension between two pillars of Greek mathematics
- Lengths constructed in Euclidean geometry are ‘real’
- Any two lengths can be measured by a common ratio.
The first of these is merely stating that the Axioms of euclidean geometry are constructive - a proof in Euclidean geometry is a step-by-step recipe to really construct some line segment, polygon, or circle. So if the axioms say you can make something, you really can make it!
Exercise 3.5 Use the constructions of the previous section together with the Pythagorean theorem to prove \(\sqrt{2}\) exists.
The second was born out by centuries of experience, in both mathematics and music all known quantities came in common ratios. Notes could be measured relative to each other, as could lengths. Ratios ruled the cosmos (today, we would say the Greeks believed in the number line \(\mathbb{Q}\) of rational numbers).
Many proofs of the irrationality of \(\sqrt{2}\) have been devised during the 2500 years since its discovery, with perhaps the most famous still being that recorded by Euclid, often phrased algebraically as proof by contradiction using fractions in lowest terms. But there are also purely geometric proofs of this fact. Below is a relatively modern one, devised by Stanley Tennenbaum around 1950.
Theorem 3.2 The Square Root of 2 is not a rational number.
Assume that \(\sqrt{2}=m/n\) is the ratio of two whole numbers, so \(2=m^2/n^2\), or \(2n^2=m^2\). Geometrically, this means there is a square with integer side lengths (\(m\)), whose area is exactly twice the area of another integer-side-length square (\(n\)).
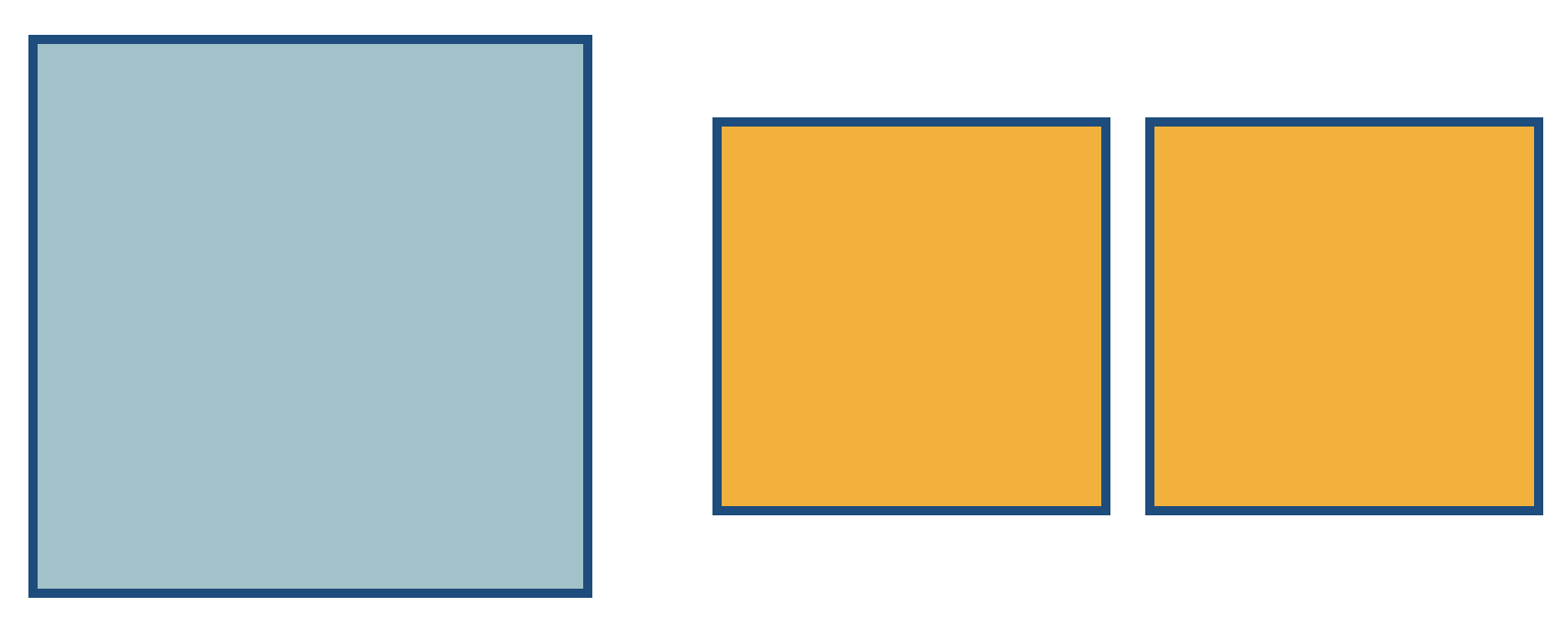
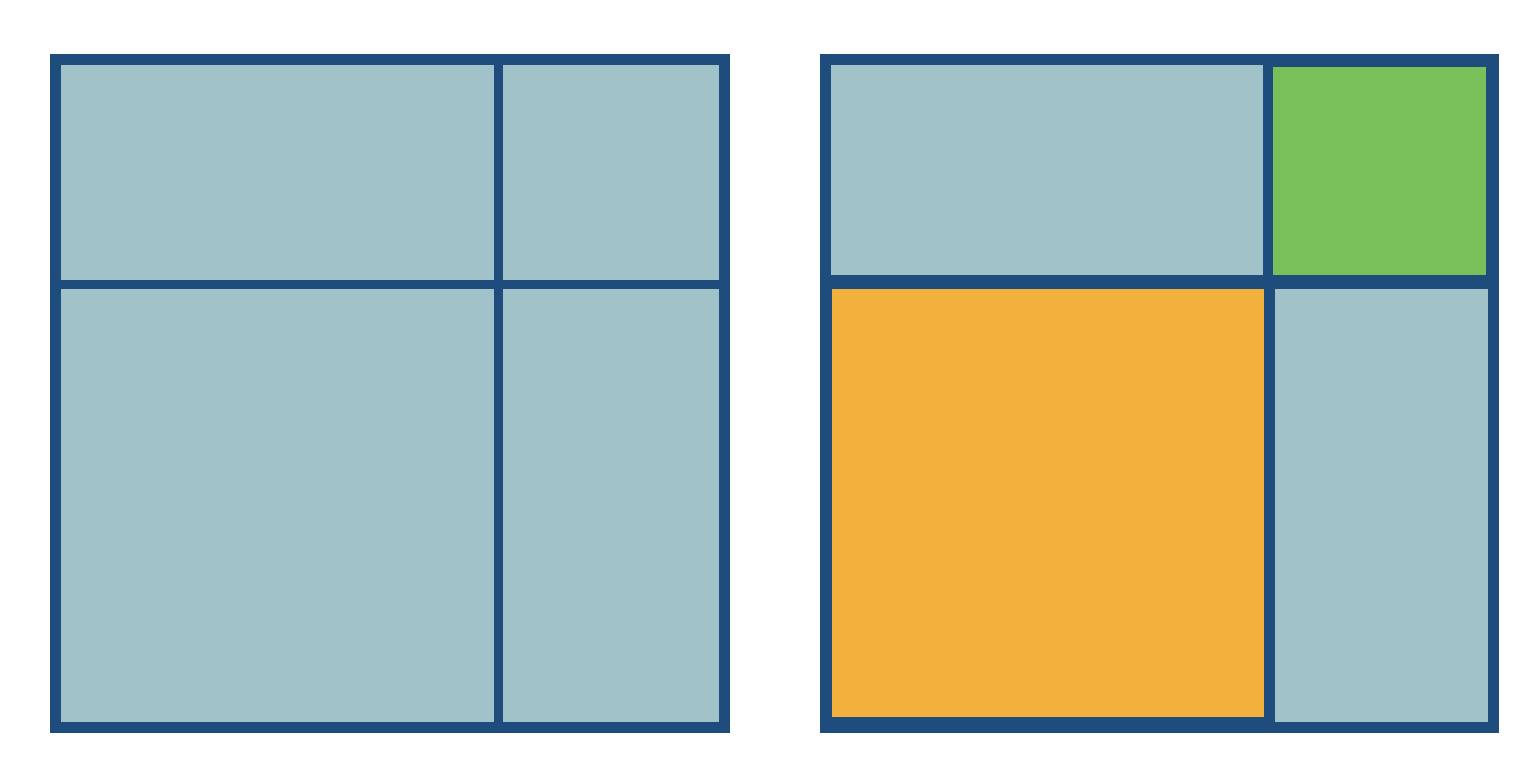
Now take the two smaller squares and position them inside the larger. They don’t fit disjointly (remember, the sum of their areas is the entire square! So if they leave any of the square unfilled they must overlap somewhere else to make up for it).
Actually, this picture determines three new squares, along the diagonal - two unfilled and one “double covered” by the overlapping yellow ones.
What do we know about these three squares? Well, they all have integer side lengths, as they are differences of integer side length squares (thus, they’re smaller) than the side lengths of our original squares. But what can we say about their areas?
The two original yellow square’s areas exactly sum to the blue squares area: this means the amount they miss (the two smaller blue squares) equals exactly the amount of overlap (the red square). So these new squares have the property that twice the area of the smaller add up to the area of the larger! This is just the start of what could easily become an infinite process: we now have a procedure that takes any integer square solution and produces a new solution with smaller squares. We could repeat this process again and again, getting ever smaller squares.
But this clearly cannot be! It is impossible to make a list of ever decreasing positive integers, as there is a smallest positive integer: one! Assuming there was any rational solution to \(\sqrt{2}=m/n\) gave us an infinite procedure to make smaller and smaller integer solutions forever, which cannot happen. Thus there cannot be any solutions at all!
And, the square root of 2 must be irrational.
Exercise 3.6 (The Square Root of 3) Construct a similar argument showing that it is impossible to find two integer side-length equilateral triangles where one has three times the area of the other.
