7 Working Infinitesimally
To use the fundamental strategy of calculus, we need to get good at zooming in - replacing a function with its linearization, as well as zooming out - putting these linearizations back together to answer our question. Fundamental to both of these tasks is understanding linear things themselves, so this is where we begin.
This class does not assume any previous knowledge of linear algebra, and we will introduce everything we need along the way (which is not that much! We will be using linear algebra as a tool, not delving into it deeply as the object of study itself). In this chapter I’ve collected the essential pieces of linear algebra that will come up throughout the course. For any of you who have taken linear algebra in the past, I would recommend you skim through this chapter to refresh your memory. For those of you who have not - there is no need to read the whole thing right now. Treat this chapter as a reference that you can return to time and again, as our toolkit in class expands. For now, its only necessary to read the section on vectors and the section on matrices.
7.1 Vectors
Vectors are a specific way to describe points in space. To picture vectors, often arrows are drawn based at a fixed point, called the origin. The length of the vector is called its magnitude, and we interpret this arrow as storing the data of a magnitude and a direction based at this origin. A one dimensional vector is an arrow on the line. If we call its origin zero, then We can think of it as ending at some particular real number: the size (or absolute value) of the number gives its magnitude, and the sign (positive or negative) is the direction.
Remark 7.1. For students familiar with linear algebra, this means we are essentially fixing the basis
Vectors do not exist all by their lonesome, but instead come together in a collection called a vector space. The subject of linear algebra is really the study of vector spaces, and the power that this level of abstraction can provide. However, we will be much more pragmatic in this course: the only vector spaces we will ever need are the spaces
Definition 7.1 (Standard Basis) For the vector space
7.1.1 Vector Arithmetic
Vectors, much like numbers, can be combined and modified using operations: they can be summed up using vector addition, and multiplied by numbers using scalar multiplication.
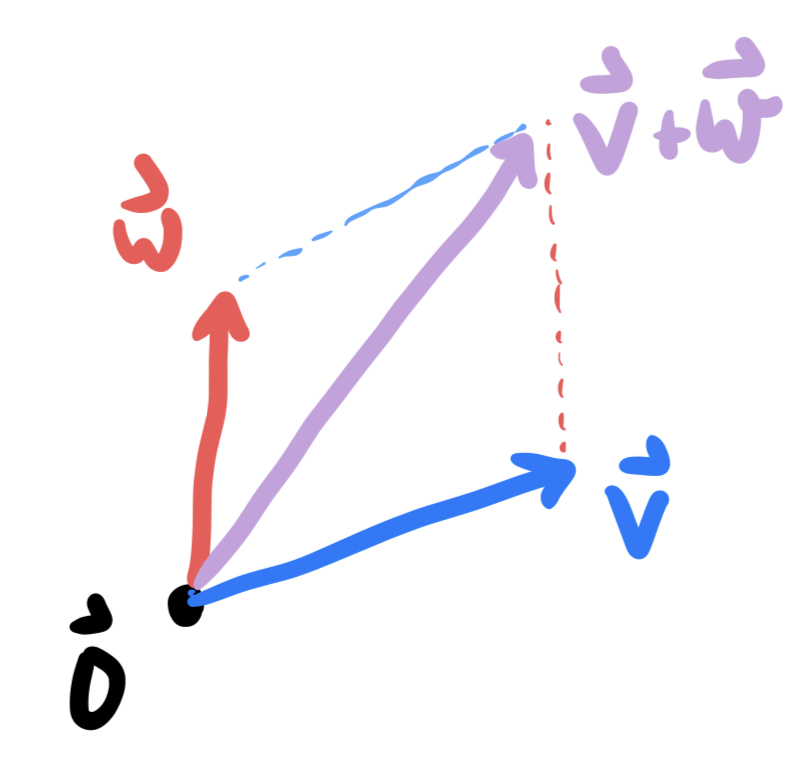
Definition 7.2 (Vector Addition) If
We will often see vector addition as a means of performing a translation: adding a vector
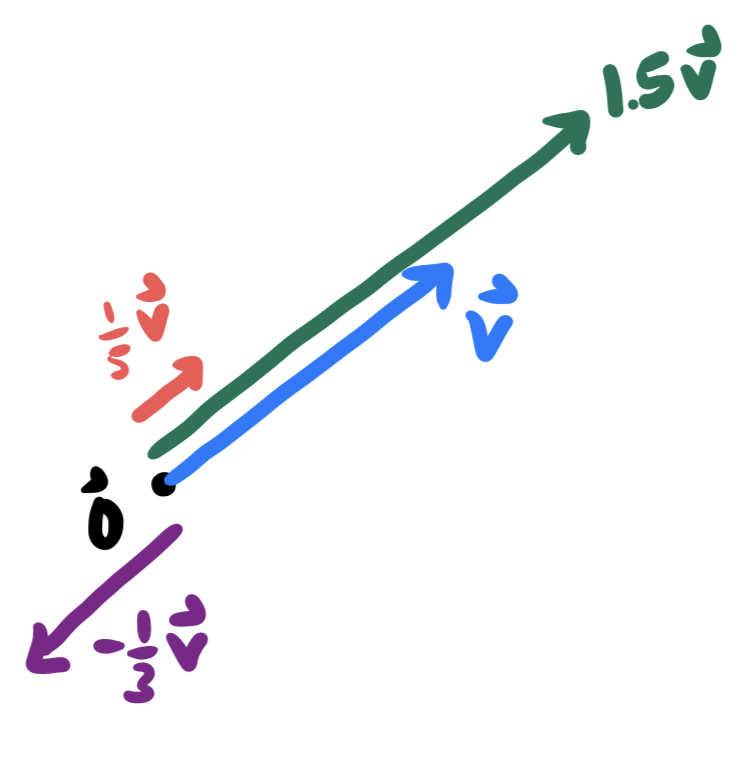
The second operation we can do to vectors is called scalar multiplication: this changes the length of a vector, without changing its direction (though, it flips the vector around backwards when the scalar is negative).
Definition 7.3 (Scalar Multiplication) If
The collection of all scalar multiples of a nonzero vector
Definition 7.4 (Affine Lines) An affine line in a vector space is a function of the form
We can refer to such a line as the line through
The Youtuber 3Blue1Brown has put together an excellent video series called the “Essence of Linear Algebra”. While much if it is beyond what we need for this course - I highly recommend watching the entire series! I’ll post throughout this article a few of the installments that are particularly relevant: here’s the introductory video on vectors.
7.2 Linear Maps
The operations of addition and scalar multiplication are of fundamental importance to vectors. Because of this, functions which play nicely with addition and scalar multiplication will
Definition 7.5 (Linear Maps) A function
- It preserves addition:
- It preserves scalar multiplication:
It’s easy to find examples of functions which are not linear: all they have to do is violate one of these two properties. For example,
Example 7.1 (1 Dimensional Linear Map) The single variable function
Of course, nothing about the 2 above is special the functions
Example 7.2 (2 Dimensional Linear Map) The function
Below is one relatively straightforward warm-up proposition using the definition of linearity, which nonetheless proves very useful: linear transformations send lines to lines.
Proposition 7.1 (Linear Maps Preserve Lines) If
Proof. This is just a computation, together with the definition of linear map and affine line. Plugging in

Here’s 3Blue1Brown’s video on Linear Transformations and Matrices: it does an absolutely excellent job of displaying the geometric meaning of linear maps we just discovered above, as well as motivating the definition of matrices (which we define below).
7.3 Matrices
Linear maps are very constrained objects: the fact that they preserve addition and scalar multiplication tells us that its possible to reconstruct exactly what they do to any point whatsoever from very little data. We will mostly be concerned with linear maps from
Say we know that
How can we figure out what happens to
We can further simplify this answer by using addition and scalar multiplication (again!):
Thus, from knowing only what
The takeaway from this computation is that remembering what a linear map does to the standard basis vectors is of fundamental importance. In fact, this is exactly what the notation of a matrix is all about!
Definition 7.6 (Matrix) A matrix is an array of numbers. The following are all examples of matrices
Definition 7.7 (Matrix of a Linear Map) If
Example 7.3 (Matrix of a Linear Map) Consider the linear transformation
Exercise 7.1 (Matrix of a Linear Map) Find a matrix for the following linear maps:
One of the best ways to understand linear maps is to visualize by hand how the transform the plane. Below is a picture drawn on the Euclidean plane.
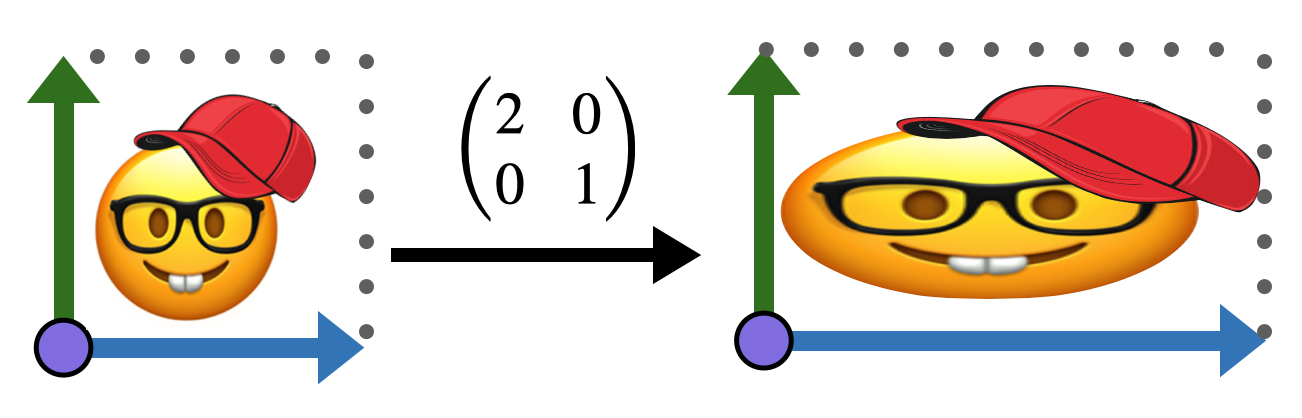
Applying the linear transformation with matrix
Similarly, the transformation
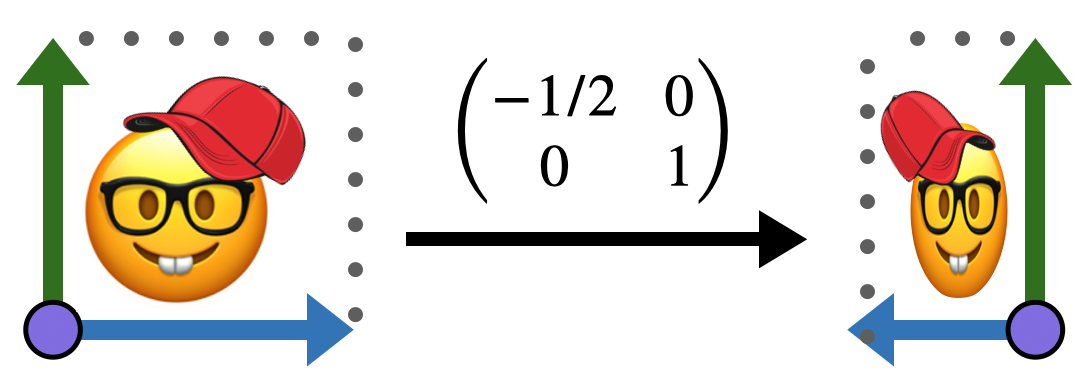
But all sorts of changes can happen! Linear maps can rotate, stretch, and squish our original square / image into any sort of parallelogram!
Exercise 7.2 Choose your own image on the plane (hand-drawn is great!), and draw a reference image of it undistorted, inside the unit square. Then draw its image under each of the following linear transformations:
7.3.1 Composition & Multiplication
Now we have at our disposal an easy-to-remember, easy-to-write notation for linear maps. All we do is store the results of the map on the standard basis! But how do we use this? How can we actually apply this linear maps to points? Looking back to our explicit example where
Definition 7.8 (Applying a Matrix to a Vector) Given the matrix
Now we know how to apply a linear transformation, but how do we compose them? If I have two linear transformations, which are each a function
Example 7.4 Its perhaps most instructive to do this directly yourself. Start with two linear transformations, say
If you keep track of what you are doing during your simplification process, you’ll notice a pattern: you can deduce the matrix for the composition directly from the matrices of the transformations themselves!
Definition 7.9 (Matrix Multiplication) If
The
Early on in the course we will not have too much use for composing linear transformations explicitly, but once we reach the chapter on hyperbolic geometry - we will find this operation extremely useful to help explore spaces we struggle to visualize.
7.3.2 Inversion
How can we undo the behavior of a linear map?
Exercise 7.3 Given linear transformation
In the exercise above, we attempted to undo the behavior of
Definition 7.10 (Inverses) If
Exercise 7.4 Try to invert the linear map from above:
If you do the above exercise carefully, you’ll find that the fact that the original linear map was
Proposition 7.2 (Inverse of a
7.4 Determinants
In the formula for inverting a linear transformation above, a strange looking linear factor showed up in front of the matrix: the reciprocal of
A linear transformation
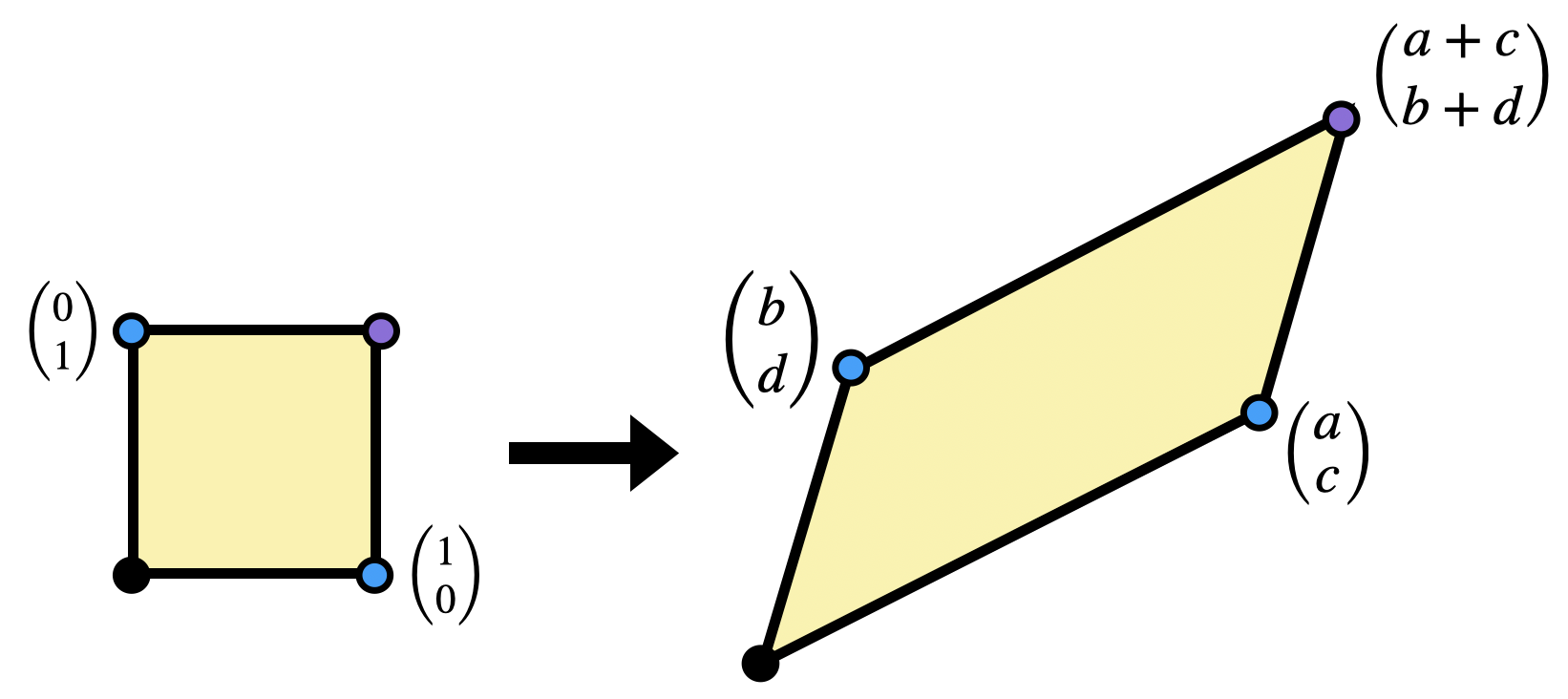
We can actually find this area in a pretty satisfying way using just what we’ve proven about Euclidean geometry so far. We know the areas of squares, rectangles, and right triangles, so let’s try to write the area we are after as a difference of things we know:
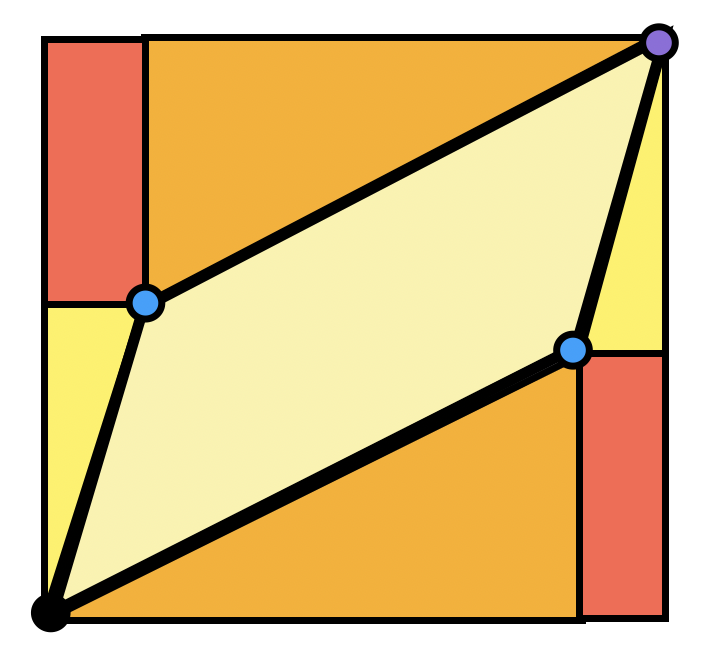
Exercise 7.5 Show the area of the parallelogram spanned by
Definition 7.11 (Determinant) The determinant of a linear transformation
Thus, the quantity we saw in the definition of the
Theorem 7.1 (Invertibility & The Determinant) A linear transformation is invertible if and only if its determinant is nonzero.
This theorem lets us think of the determinant as a tool to detect invertibility. If the determinant is zero, then the linear transformation takes a square to something of zero area: a point, or a line segment! And then information has been lost - the square has been crushed onto a smaller dimensional space - and there’s no undoing that.
So far we’ve figured out the meaning of the determinant when it is a positive number. But it can also be negative: what does it mean to scale area by a negative number? It’s easiest to see via an example - the matrix

We often refer to this concept formally with the term orientation. We say a function is orientation preserving if it does not reflect, or flip an image, and orientation reversing if it does. Thus, the determinant is not only an invertibility detector, but an orientation detector as well.
Definition 7.12 (Orientation Preserving) A linear transformation is orientation preserving if its determinant is a positive number.