12 Lines
Laying down the foundations at a deeper level than the Greeks, we have some work to do before we can hope to recover the axioms of Euclid. Indeed - no where in our foundations does the term line even appear: we are in the awkward position of being able to work with any curve we like, but we do not know which among them is a straight line!
To find the lines among the sea of curves, we need a good and precise definition. Definitions single out an important property characterizing the object being defined, and for that definition to be good, we would like that condition to be checkable within the framework we are building. So - Euclid’s definition of a line as a breadthless length is not going to do much for us here.
However, looking to history, we find several good candidate definitions among the properties of lines the ancients took as essential.
Definition 12.1 (Essential Properties of Lines)
Archimedes used as an axiom of length that the line segment between two points is the shortest among all curves connecting them. This could be turned upside down and directly used as the defining feature of lines: whichever curve is shortest, we call a line.
As a followup to the infamously unhelpful breadthless length Euclid states the important feature of a line being that the points lie evenly with themselves. This also requires a bit of translation, but if we can define what it means for a curve to turn, we could then specify straight lines as curves that do not turn.
The term line also shows up in phrases such as line of symmetry - for instance in discussing that the human form is left-right-symmetric. The fact that reflections fix a line is foundational to geometric arts like Origami, which is what allows the use of Euclidean geometry to describe the collection of creases made: they arise as lines of symmetry, so they are the lines of Euclid!
In fact all three of these things can be made into precise statements in our new geometry, and we can compute exactly what sort of curves satisfy each of them. The main purpose of this section is to do so, and to show that all three of them end up specifying exactly the same class of curves! This is one reason that lines are so important to geometry: they are the single objects sharing all three of these very natural properties!
12.1 Shortest
We start first with the insight of archimedes, and attempt to make precise the notion of shortest curve between two points. In doing so, we will actually first define line segment, and then use this to define lines more generally.
Definition 12.2 (Line Segment) Given two points

This definition seems very powerful: if you know something is a line segment you know a lot about it: you know how its length relates to the length of every single other curve!
Theorem 12.1 (Segments of
Proof. First, we compute the length of the
This of course is unsurprising! But its good to know explicitly that we have found a curve of length exactly
Our goal is now to show that
but this is essentially all we know. Nonetheless, let’s push onwards and see what we can learn about
Now we do some estimation: we know that whatever
We can then take the square root of both sides of this equation (which preserves inequalities) to get
Igoring all the middle terms in this string of inequalities, (and recalling the left hand side is the norm of
Thus, as functions of
But now we have really made some progress: on the right side here we are integrating a derivative, so we can use the fundamental theorem of calculus! The antiderivative of
And with that, we’ve done it! The integral on the left side was precisely the length of
Now that we have a firm understanding of segments, how can we properly bootstrap this idea to a definition of lines? A line itself has no endpoints, and so is not a distance minimizing curve! However, it has the property that if you cut out any segment from it, that segment is distance minimizing. To say this formally, we need a word for “cut out a segment of a curve”
Definition 12.3 (Finite Segment of a Curve) Given a curve

This makes the definition for a line completely precise:
Definition 12.4 (Line) A curve
This sounds pretty useless until we unpack it: since line segments are distance minimizers, this is saying that to be a line, a curve must have the property that it is distance minimizing between any two points it passes through! A strong condition indeed.
However, given the work we did above on segments of the
Corollary 12.1 (The
Well, after all this theory we have finally managed to track down one line in the plane! How can we find more? One option of course is to mimic the argument given here: with trivial modifications we can similarly prove that the
Instead, we take this as our first opportunity to use one of the most powerful ideas in modern geometry: symmetry. We proved that isometries preserve the length of all curves, and this has an important consequence: isometries send lines to lines!
Theorem 12.2 (Isometries Send Lines to Lines) Let
Proof. To argue that
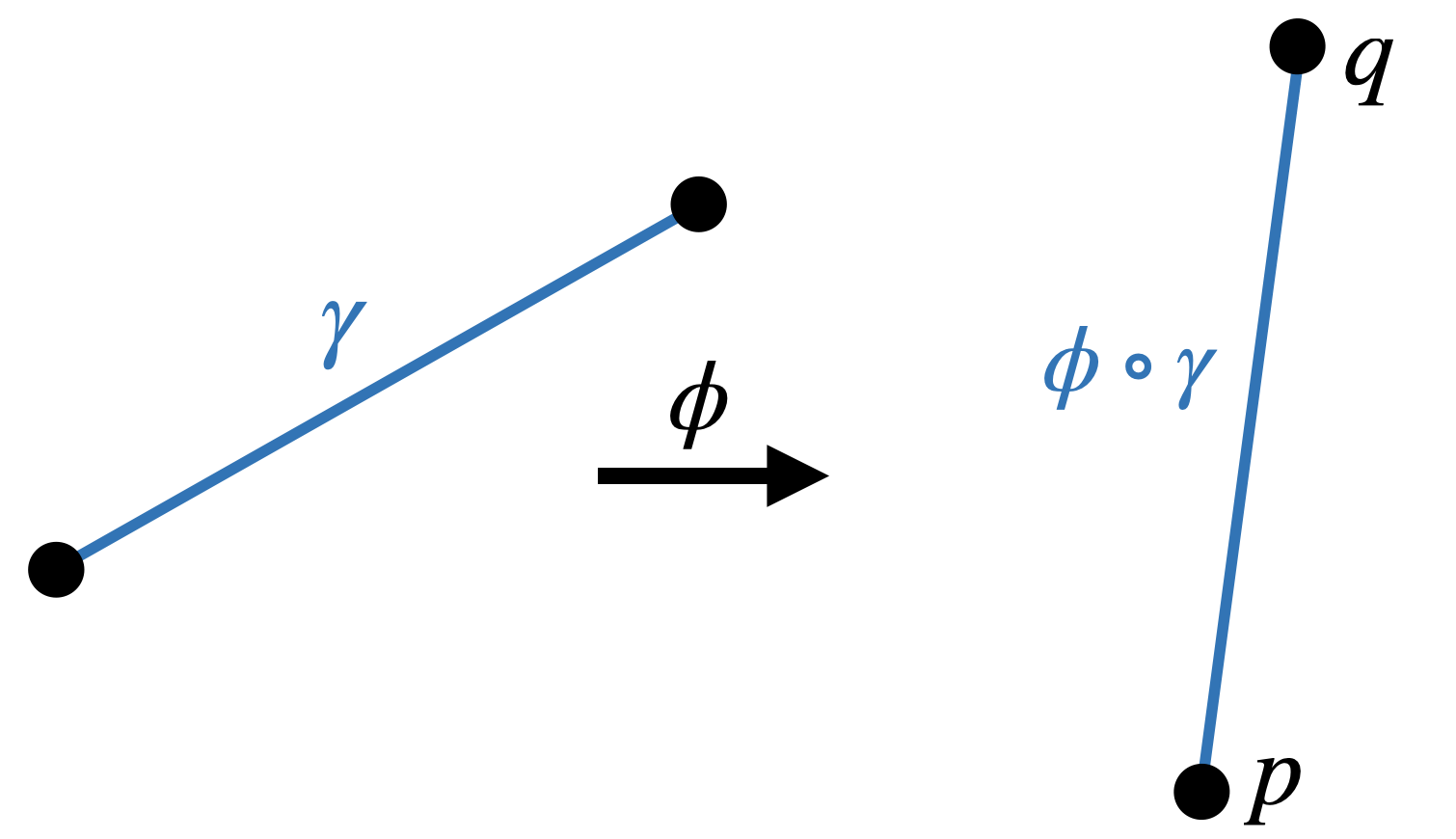
Assume for the sake of contradiction that this is not length minimizing: then there is some other curve

Now, apply the inverse function

Since isometries preserve length, we know that since
Thus, its impossible that
This gives us an easy prescription to track down lines: we already know
Corollary 12.2 (Affine Equations are Lines) Every linear equation
Here we concentrate on the main case where
Proof. Then, the rotation
Thus,
If
Since we know that the length of curves does not depend on their parameterization, we can speed up or slow down
We saw in Theorem 12.2 that any isometry will carry a line to another line. The same is true more generally of similarities:
Exercise 12.1 (Similarities Send Lines to Lines) Let
*Hint-replicate the proof of Theorem 12.2 as closely as possible, replacing the isometry
Using these tools, we can already start our process of rebuilding the Elements from below!
Theorem 12.3 (Proving Euclid’s Axiom I) Given any two points
Proof. Knowing that line segments are given by affine equations, we need just fine an affine equation
Theorem 12.4 (Proving Euclid’s Axiom II) Given a line segment between two points of
Proof. Let
The result is still an affine equation on a closed interval, and so still is a line segment by Corollary 12.2. And, as
12.1.1 Uniqueness of Lines
Above we proved the existence of lines, and found that all affine equations describe lines in the plane. But are these all the lines there are to be found? In fact they are - and we can confirm this with very little extra work: we had all the ideas in place already during the proof of Theorem 12.1.
Proposition 12.1 Segments of the
Proof. Let

But, this means that
And, re-arranging the integral, this immediately implies
Applying isometries to this, we can extend this result to any of the segments we already know:
Exercise 12.2 Prove that all Euclidean lines are given by affine equations. Hint: we already know that the affine equation
12.2 Straightest
Another notion of line is “curve that doesn’t turn”. How do we make this precise? The unit tangent vector to a curve gives its direction, so we say a curve “turns” if the tangent changes direction.
The derivative of the tangent vector is acceleration, a “straight curve” would have acceleration zero.
Definition 12.5 (Straight) A curve
Remark 12.1. You might worry what it means to say that tangent vectors are constant, since each one of them technically lives in a different tangent space! This difficulty will be absolutely crucial to deal with later on, when space itself is curved. But here in
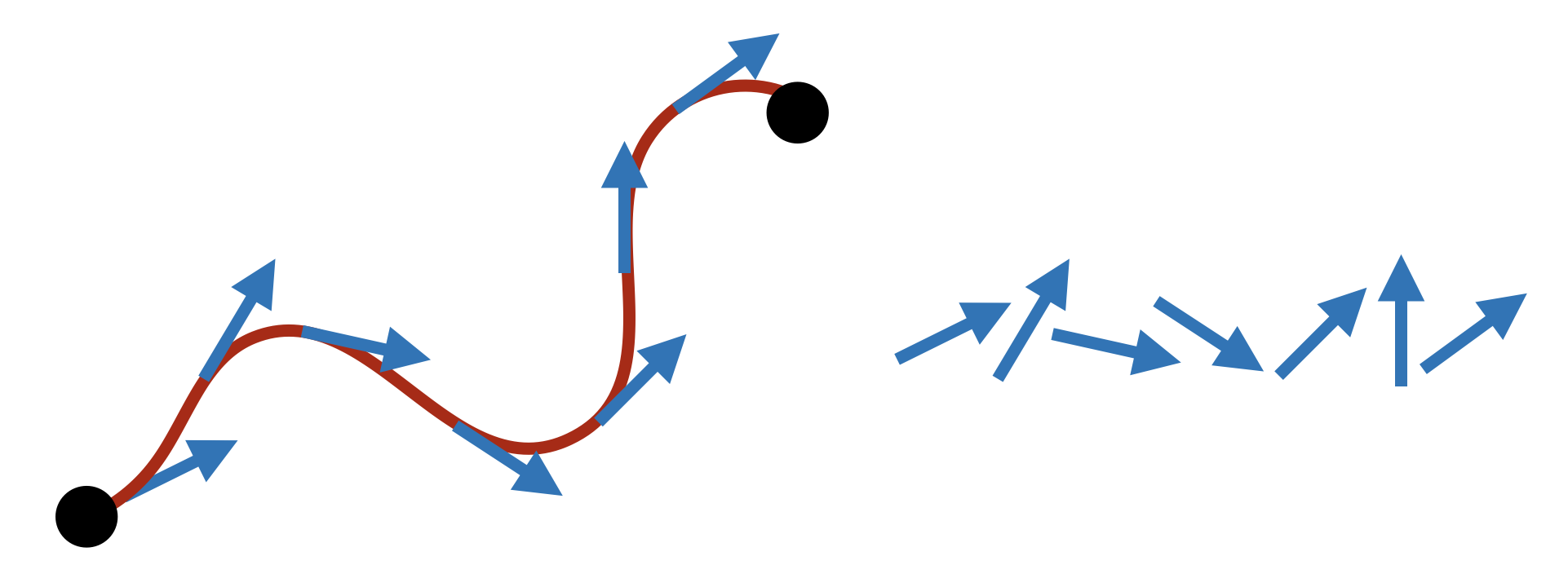
We’ve already done all of the hard work above, and we can now quickly confirm that this alternative definition picks out exactly the same class of curves.
Theorem 12.5 (Distance Minimizers are Straight) A curve
Proof. This is a direct computation, now that we’ve proven that every distance minimizer is given by a linear equation
To prove the other direction, we now assume we start with a straight curve
This will turn out to be true in general: while we will have to be a little more careful when moving onwards to other geometries, curves that are straight will coincide with curves that minimize distance.
12.3 Folding
Finally we come to the third possible definition of line, and show that it also picks out the same collection of curves!
Definition 12.6 (Line of Symmetry) A fixed point of an isometry
A curve
This captures the intuitive notion of a crease from folding paper, or reflecting across a line: this swaps the two sides of the plane but leaves What are the fixed sets of reflections?
Proposition 12.2 (Reflecting in the
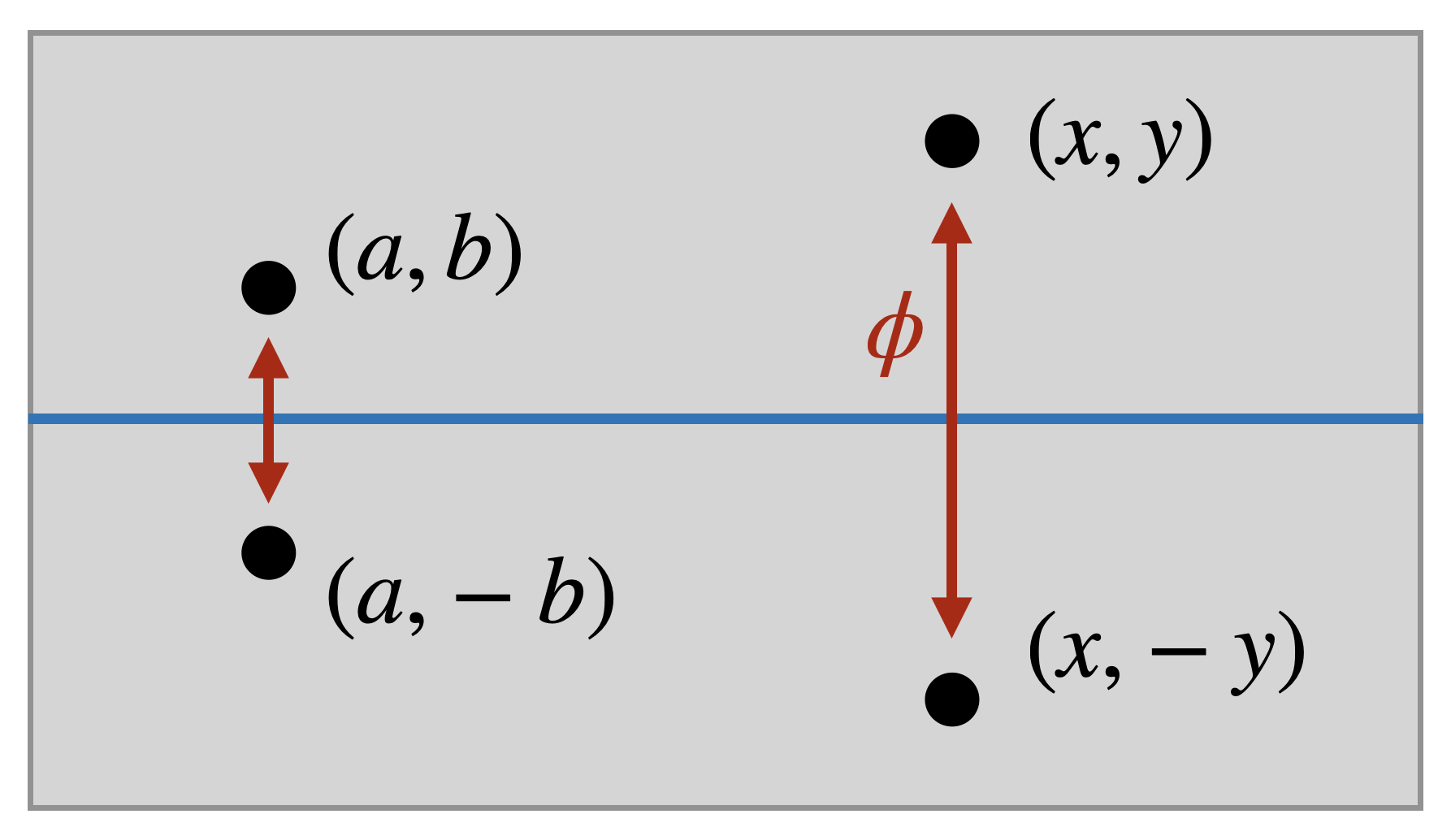
Proof. First, notice that
Since
Let
This map fixes the line of points
Exercise 12.3 (Reflections in Any Line) Prove that every affine curve is a line of symmetry. Hint: given an isometry that reflects in the
The converse is also true: that every line of symmetry is an affine equation: so this characterization of lines exactly agrees with the two previous. To prove this, we will need a bit better understanding of the isometries of Euclidean space, and so will postpone until that chapter,
12.4 Distance
So far in our development of Euclidean geometry, we have defined the length of a curve, but we have not defined any notion of distance between two points. This makes some sense, as the distance between two locations depends on how you get from one to the other, and that’s exactly what our definition captures!
However, now that we know there is a unique shortest curve between any two points, there’s a natural candidate for distance: the shortest possible path.
Definition 12.7 (Distance) The distance between two points
Because of all of our hard work above, we can turn this rather abstract definition into something concrete and practical!
Theorem 12.6 (The Euclidean Distance) Let

Proof. We can write down a distance minimizing curve from
Proposition 12.3 (Distance is preserved by isometries) If

Proof. First, we start with the isometry case. Given two points
Applying
Exercise 12.4 If
Hint: follow closely the argument for isometries above, replacing the theorems relating isometries, line segments, and lengths with the corresponding results for similarities.

It will often be useful to measure distances not just to points, but to more complicated objects in the plane.
Remark 12.2. We are avoiding a detail here, that anyone who has seen real analysis may be interested in. Sometimes, the minimum distance between
Definition 12.8 (Distance to a Set) Let

12.4.1 Useful Computations
'Now that we know exactly what lines are, we can convert elementary geometric problems - such as when they intersect - into algebraic problems, solvable via systems of equations. Here’s an example.
Exercise 12.5 (Intersecting Lines) Calculate the point of intersection between two lines
With the ability to solve equations (since lines are given by affine equations, which are easy to work with!) we have developed a geometric superpower. To demonstrate this, we can use this to prove Playfair’s axiom (remember, this is equivalent to Euclid’s 5th Postulate!)
Proposition 12.4 Given any line
Exercise 12.6 Prove Proposition 1.
Hint: use isometries to help you out!
First, use an isometry to move
In addition to algebra, founding our new geometry on calculus makes all of these tools also available to us. As a first example, we will use our knowledge of derivatives to minimize the distance between a point and a line. Minimizing distance turns out to be a pretty common thing one needs to do in applications of geometry, and while straightforward theoretically (take the derivative, set it equal to zero), its annoying in practice because of the square root in the distance formula. But there is a nice trick to get around this:
Exercise 12.7 (Minimizing the Square: A Very Useful Trick!) Let
First, assume
Conversely, assume
This tells us anytime we want to minimize a positive function, we could always choose to find where its square is minimized instead, if that turns out to be easier. The main question is below, where without loss of generality we have taken the point to be the origin (as we could always slide it there via an isometry).
Exercise 12.8 (Closest Point on Line) Let
Hint: use calculus to find the closest point on