Assignments
Problem Set I
Exercise 1 (Constructing an Isoceles Triangle) Start with a line segment of length
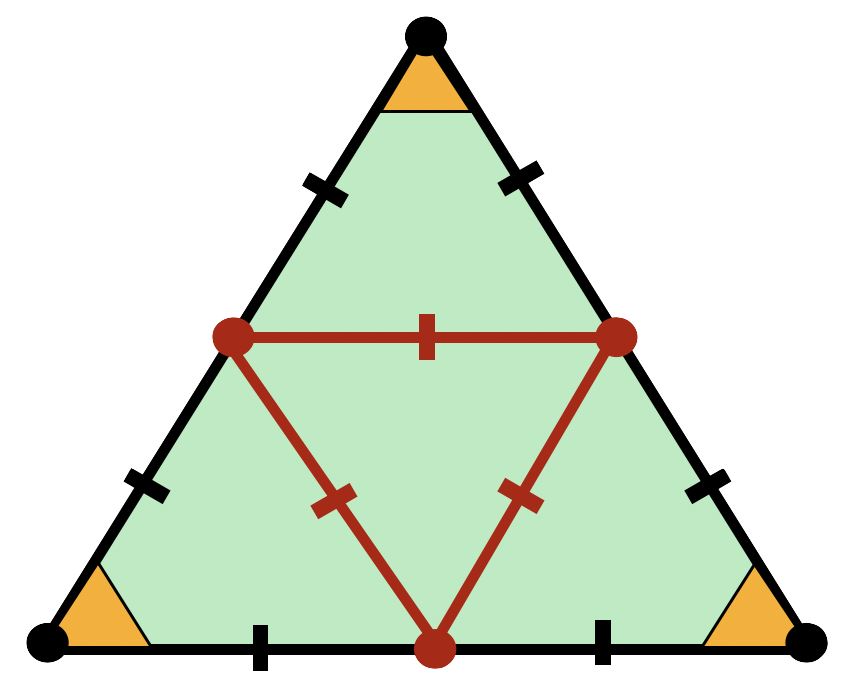
Exercise 2 (Inscribing an Equilateral Triangle) Prove that inside of an equilateral triangle, you can inscribe an upside down equilateral triangle of exactly half the side length, shown
Exercise 3 (Angle Sums of Polygons) A polygon is convex if all of its angles are less than
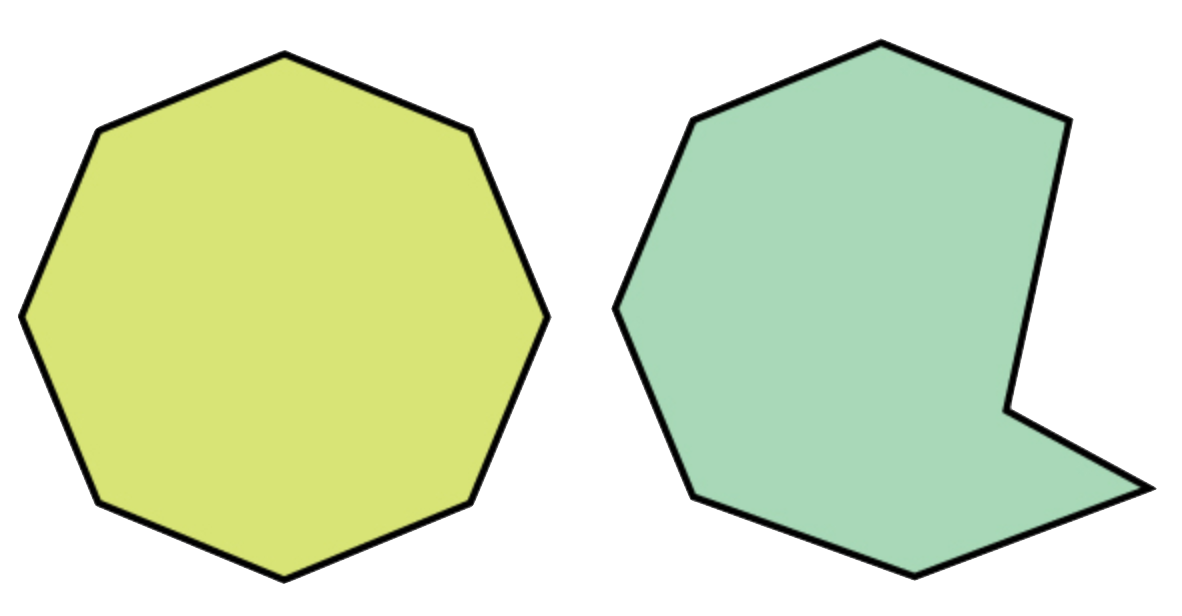
Prove that the angle sum of convex quadrilaterals is a constant, for all quadrilaterals. Prove the angle sum of convex pentagons is also a constant. What are these constants?
What do you think the formula is for the sum of angles in a convex
Exercise 4 (Rectangles Exist) Prove that Rectangles exist using Euclid’s Postulates (and also Playfair’s Axiom, if you like it), and the propositions proven in the sections Euclid and Parallels.
Hint - we know how to make right angles now, and parallel lines through points. Start making some!
Exercise 5 (Diagonal Bisectors) If the diagonals of a quadrilateral are bisect one another, then that quadrilateral is a parallelogram.
Exercise 6 (Proving the Pythagorean Theorem) The following is an ingenious rearrangement proof of the Pythagorean theorem.
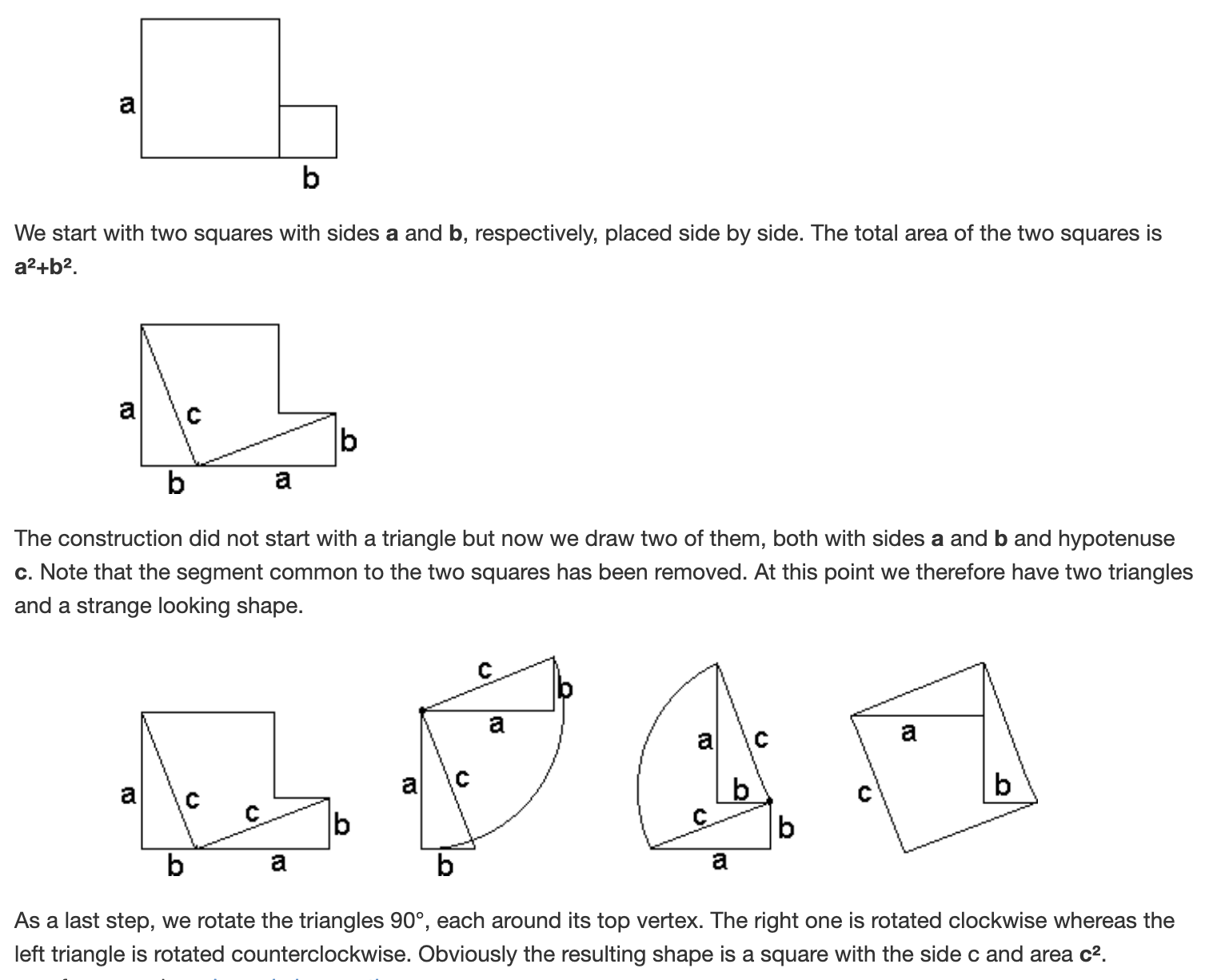
Prove that the final shape shown here is a square, using what we have learned (the Postulates and Propositions).
Problem Set II
Exercise 7 (The Square Root of 3) Read carefully the geometric proof of Theorem thm-sqrt2-irrational, which proves
Construct a similar argument showing that it is impossible to find two integer side-length equilateral triangles where one has three times the area of the other.
Hint: try to mimic the argument in the book, but now use the diagram below for inspiration

Exercise 8 (Convergence to the Diagonal) Consider a simpler analog of Archimedes’ situation, where instead of trying to measure a curve using straight lines, we are trying to measure a straight diagonal line using only horizontal and vertical segments. The following sequence of paths converges pointwise to the diagonal of the square, but what happens to the lengths?

If you believed that because this sequence of curves limits to the diagonal, its sequence of lengths must limit to the length of the diagonal, what would you have conjectured the pythagorean theorem to be?
Exercise 9 Use the result of last week’s problem Exercise Inscribing an Equilateral Triangle (that you can inscribe an equilateral triangle with half the side lengths) to produce an alternative proof of Archimedes sum

Exercise 10 Construct an argument in the same spirit as Archimedes’ geometric series to show the following equality:
Fractals
The final two problems involve the Koch Snowflake fractal. In these problems you should still explain why things you are doing are valid geometrically, but you do not need to prove every thing you do from the axioms. We are getting ourselves ready for a calculus mindset!
This shape is the limit of an infinite process, starting at level

Doing this to every line segment quickly turns the triangle into a spiky snowflake like shape, hence the name. Denote by
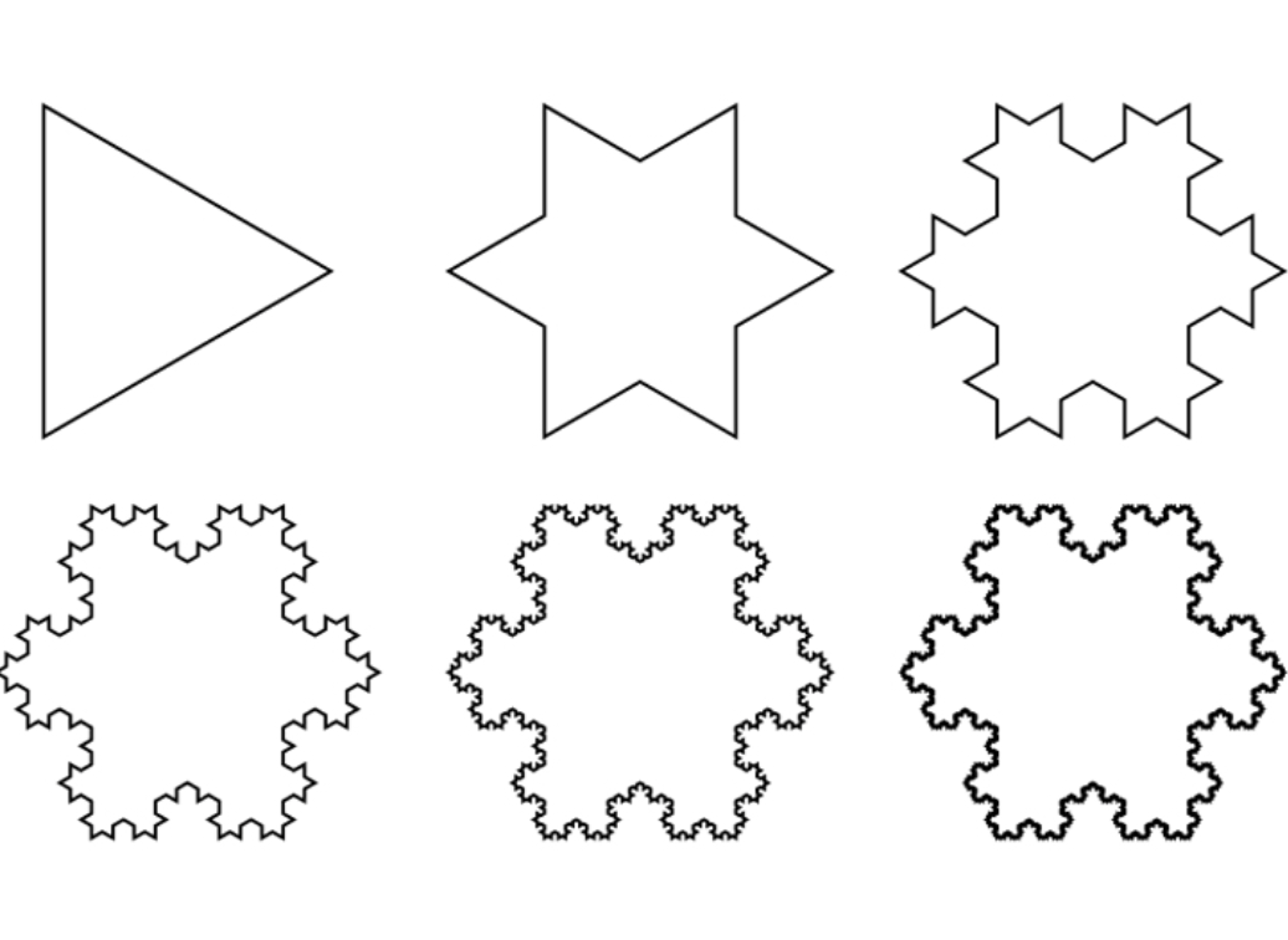
Say the initial triangle at level
Exercise 11 (The Koch Snowflake Length) What are the perimeters
Explain why as
Before doing the next problem: ask yourself what happens to the area of an equilateral triangle when you shrink its sides by a factor of 3? Can you draw a diagram (similar to that from last week’s Exercise Inscribing an Equilateral Triangle but larger) to see what the ratio of areas must be?
Exercise 12 (The Koch Snowflake Area) What are the areas
Find an infinite series that represents the area of the
Problem Set III
Linear Transformations
This exercise goes with similar examples in the text, on visualizing linear transformations action on the plane by what they do to the points of the unit square. For instance, we saw that the transformation
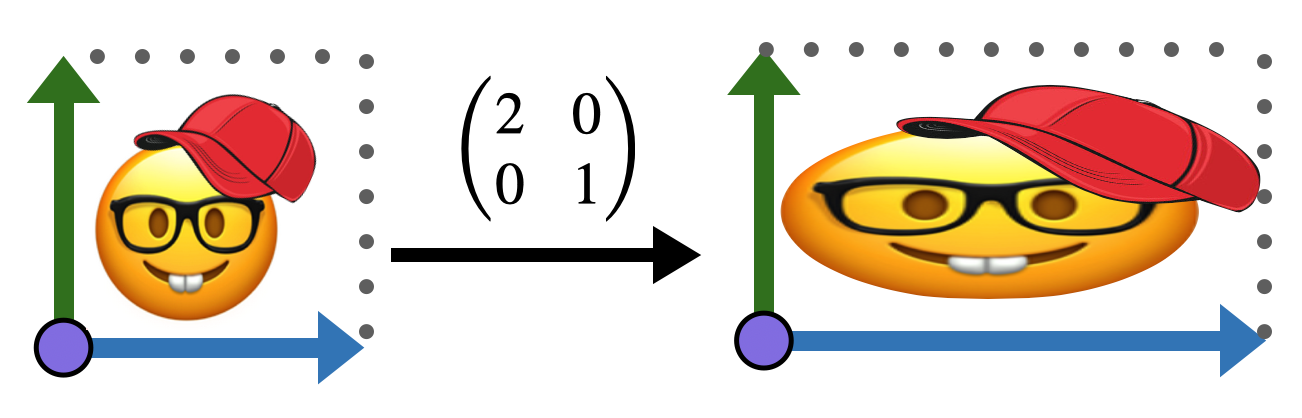
Exercise 13 Choose your own image on the plane (hand-drawn is great!), and draw a reference image of it undistorted, inside the unit square. Then draw its image under each of the following linear transformations:
Determinants & Area
Recall the following definition: the determinant of a linear transformation
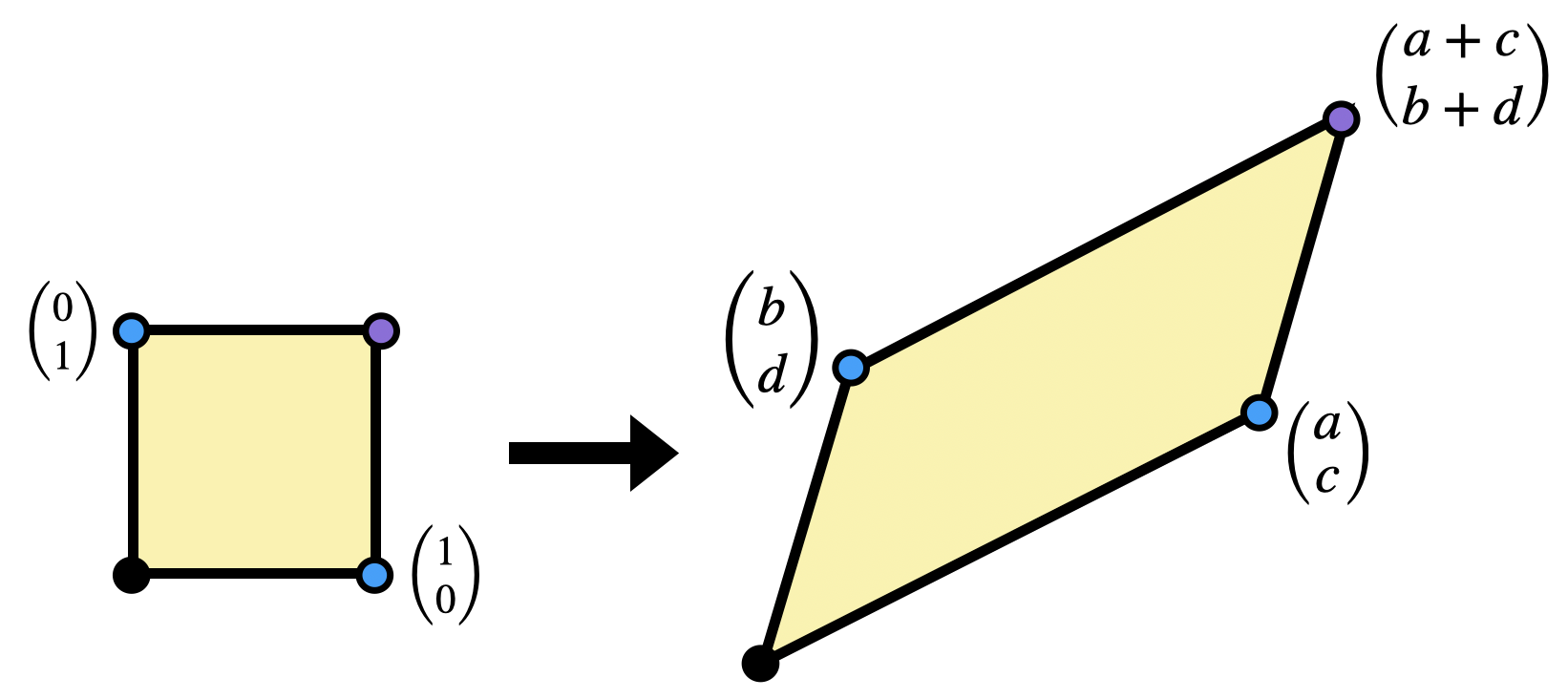
In class, said this measured the area change of the unit square under the linear transformation
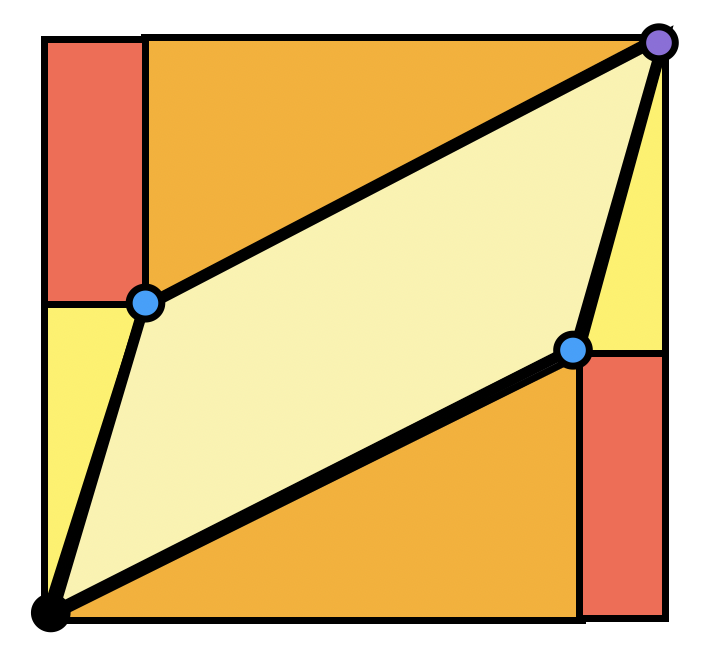
Exercise 14 Show the area of the parallelogram spanned by
Calculating Derivatives
Practice calculating the derivative of multivariate functions as matrices, and applying them to vectors. No proofs, here, just some computations!
Exercise 15 Find the derivatives of the following functions, at the specified points.
- The function
- The function
Now use these to compute the following quantities:
Differentiating Compositions
This is another problem which focuses on the new computational skills, using linear algebra. No proofs here either!
Exercise 16 If
Differentiate the following compositions:
When the Derivative is Constant
In class, we proved that if a function is linear, then its derivative is constant. But is this the only time a function’s derivative is constant? Certainly no - the derivative of
We call a function affine if it is the composition of a linear function and addition of a constant. For instance,
Exercise 17 (When the derivative is constant) Prove that a function
Hint: if the derivative is a constant matrix, can you integrate each entry (with respect to the right variable) to figure out what the original functions were?
Problem Set IV
Parameterization Invariance
Below are four different curves which all trace out the same set of points in the plane: the segment of the
Because these all describe the same set of points, we of course want them to have the same length! But our definition of the length function involves integrating infinitesimal arclengths (derivatives), and these curves don’t all have the same derivative! Thus, to really make sure our definition makes sense, we need to check that it doesn’t matter which parameterization we use, we will always get the same length.
Exercise 18 Check these three parameterizations of the segment of the
After doing this exercise, read the proof of Theorem Length & Parameterization Invariance (which follows this exercises’ original location in the text): you don’t have to write anything here, but it’s good to see how do to this in general with the chain rule!
Non-Isometries
Exercise 19 Write down a linear map that sends both
This shows there’s not a shortcut to checking something is an isometry by just seeing what happens to the basis vectors!
Composition and Inversion of Isometries
Exercise 20 If
Remember, you will need to explain why at every point
Homogenity and Isotropy
In class we built a couple different sorts of isometries from the basic ones we constructed by hand (translations and rotations about 0). In this exercise, you are to prove the existence of another very useful isometry. We will use this homework problem all the time
Exercise 21 (Moving from
Hint: try to combine pieces we know about, and prove the result does what you need by applying it both to the point
Lines of Symmetry
In this exercise we will investigate the third potential definition of line, which involves isometries.
Definition 1 (Line of Symmetry) A fixed point of an isometry
A curve
In this exercise, you show that the curves which are lines of symmetry are exactly the same as the curves which are lines under Archimedes’ definition!
Exercise 22 (Reflections in Any Line)
Show that map
Show that every curve which is distance-minimizing in the plane is also a line of symmetry. Hint: given an isometry that reflects in the
Equilateral Triangles Revisited
In this question we will revisit two problems from Greek geometry. That is we will be re-proving things we knew before, so we know they are still true in our new foundations!
This problem requires the distance function on the Euclidean plane, which we did not get to in class on Thursday, but will cover on Tuesday. However - you all areadly know the distance function so you can absolutely complete the homework now if you like!
Definition 2 If
First, we re-prove the very first proposition of Euclid, the existence of an equilateral triangle. Then we redo your earlier homework problem on finding a smaller equilateral triangle inside of it, of half the side lengths (but this is much easier with our new tools!).
Exercise 23
Beginning with the segment
Re-prove that inside of this equilateral triangle, you can inscribe a smaller one with exactly half the side length. Hint: just find where the vertices should be, and then measure the distances between them!
Length of a Parabola
Arclength integrals give a good opportunity to practice a lot of Calculus II integration techniques. Even for relatively simple curves like the parabola, the answers can be quite nontrivial!
Exercise 24 (The Length of a Parabola) Find the length of the parabola
- Paramterize the curve as
- Perform the trigonometric substitution
- Let
- After parts, use the trigonometric identity
- Get both copies of
- Relate this back to your original integral, and undo the substitution
- Finally, you have the antiderivative in terms of
Minimizing a Function by Minimizing its Square
Here’s a problem that’s straight up single variable calculus, but turns out to be a quite useful “trick” in geometry! Oftentimes we want to minimize a function in geometry (like arclength, or distance) but this turns out to be technically hard because of the square root. One might wonder - what happens if I square the function, and try to minimize that instead? That will have an easier formula (no roots), but will I get the right answer?
This exercise shows, yes you will!
Exercise 25 (Minimizing the Square: A Very Useful Trick!) Let
First, assume
Conversely, assume
Problem Set V
The Parallel Postulate
Recall that Playfair’s Axioms (already suggested by Proclus in the 400s) was a simpler re-phrasing of Euclid’s original fifth postulate on parallel (that is, nonintersecting) lines.
Proposition 1 Given any line
Exercise 26 Prove Proposition prp-proving-playfairs-axiom.
Hint: use isometries to help you out!
First, use an isometry to move
Similarities and Lines
We saw in Theorem Isometries Send Lines to Lines that any isometry will carry a line to another line. The same is true more generally of similarities:
Exercise 27 (Similarities Send Lines to Lines) Let
*Hint-replicate the proof of Theorem Isometries Send Lines to Lines as closely as possible, replacing the isometry
Distance to a Line.
In this problem it’s probably helpful to use the ‘calculus trick’ offered as an optional problem last week: that is, if you are looking to minimize a positive function
The reason this is useful to us is that the distance function in geometry has a square root in it, and differentiating roots can be a lot of work. So this says instead we can minimize the square of distance to find the right point.
Exercise 28 (Closest Point on Line) Let
Alternatively, do this for the line
- Find the point
- Calculate
- What angle does the segment connecting
This problem shows how we can use calculus as a tool to discover a geometric fact: here we learned something about where the closest point on a line is located (by finding it with calculus, then calculating the angle formed).
Often calculus can provide the tools needed for discovery of a new fact, but once its known, one can often go back and find a geometric (more in the style of Euclid) proof that all of a sudden makes the conclusion feel inevitable.
Exercise 29 (Closest Point: Geometric Reasoning) Now that we know the answer, formulate in your own words a geometric proposition that describes which point
Prove this propostion without just taking a derivative, try to reason more like the Greeks, using other facts and theorems that we’ve proven.
Hint: if you pick some other point
Intersecting Circles
Recall that in all of Euclid’s axioms, conditions for intersections with circles were never specified! Indeed - Euclid intersected two circles in his construction of the equilateral triangle. Now that we have a precise description of circles in our new foundations, we can fix this gap:
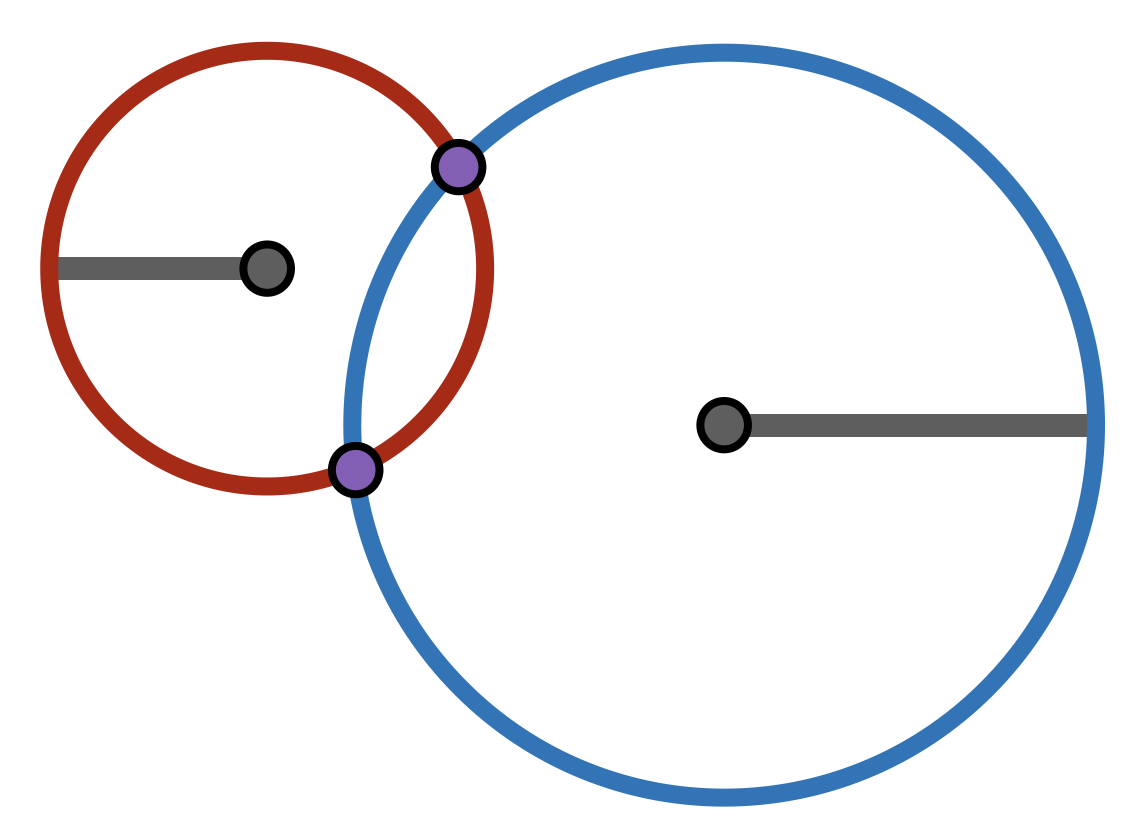
Exercise 30 Prove that two circles intersect each other if the distance between their centers is less than or equal to the sum of their radii.
Alternatively: do this for the specific case where the circles radii are 3 and 4, and the distance between thier centers is 5.
Hint: start by applying an isometry to move one of the circles to have center
Parabolas
A parabola was one of few curves that the Greeks understood. However, while we often think of a parabola algebraically that was not their original definition!
Definition 3 (Parabola) Given a point
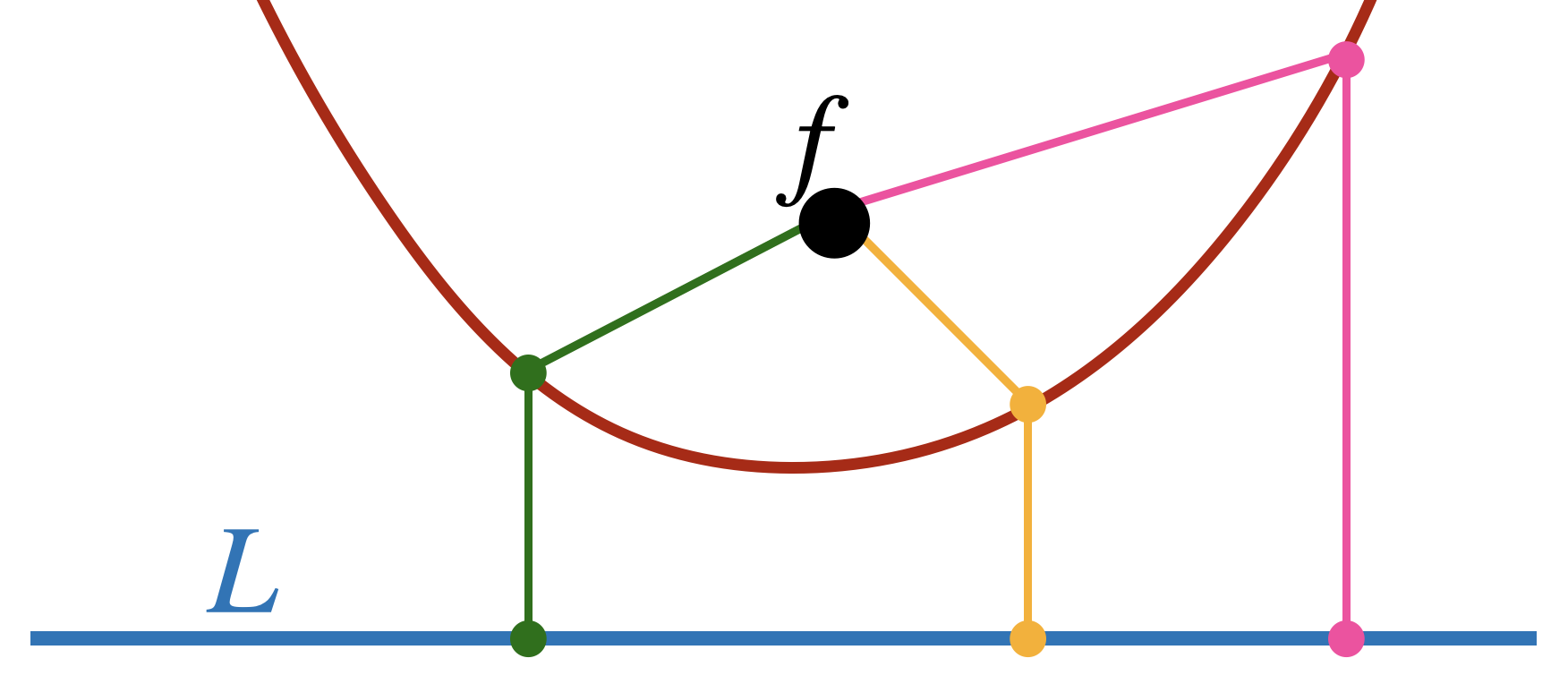
Exercise 31 In this problem we confirm that
- Write down an algebraic equation for the coordinates of a point
- Find which point
Problem Set VI
Right Angles
In this set of two problems, we make use of the fact that we can finally measure angles rigorously in our new geometry, to reprove an important fact we already know, and to prove the one remaining postulate of Euclid: the 4th.
Exercise 32 Prove that rectangles exist, using all of our new tools! (Ie write down what you know to be a rectangle, explain why each side is a line segment, parameterize it to find the tangent vectors at the vertices, and use the dot product to confirm that they are all right angles).
To prove Euclid’s 4th postulate, we need to first phrase it more precisely than Euclid’s original all right angles are equal.
Proposition 2 (Euclids’ Postulate 4) Given the following two configurations:
- A point
- A point
There is an isometry
Exercise 33 Prove Euclids’ forth postulate holds in the geometry we have built founded on calculus.
Hint: there’s a couple natural approaches here.
- You could directly use Exercise Moving from p to q. from a previous homework to move one point to the other and line up one of the tangent vectors. Then deal with the second one: can you explain why its either already lined up, or will be after one reflection?
- Alternatively, you could show that every right angle can be moved to the “standard right angle” formed by
Measurement of the Circle
The half angle identities played a crucial role in Archimedes’ ability to compute the preimeter of
By repeatedly bisecting the sides, we can start with something we can directly compute - like a triangle, and repeatedly bisect to compute larger and larger
In the book, I use the half-angle identities to compute the exact value of
Exercise 34 Continue to bisections until you can compute
Explain how we know that this is provably an underestimate of the true length, using the definition of line segments.
Optional: Be brave - and go beyond Archimedes! Compute the circumference of the 192-gon.
Quadrature of the Parabola
This is also a two-problem series, where we complete Archimedes famous Quadrature of the Parabola using modern tools from calculus. Archimedes problem was about a parabolic segment: that is, the region enclosed by a parabola and a line segment connecting two points on the parabola. Instead of working in complete generality like Archimedes, we will be content to just study a special case in this problem. We will look at the parabola

Recall Archimedes main result: the area of this parabolic segment is
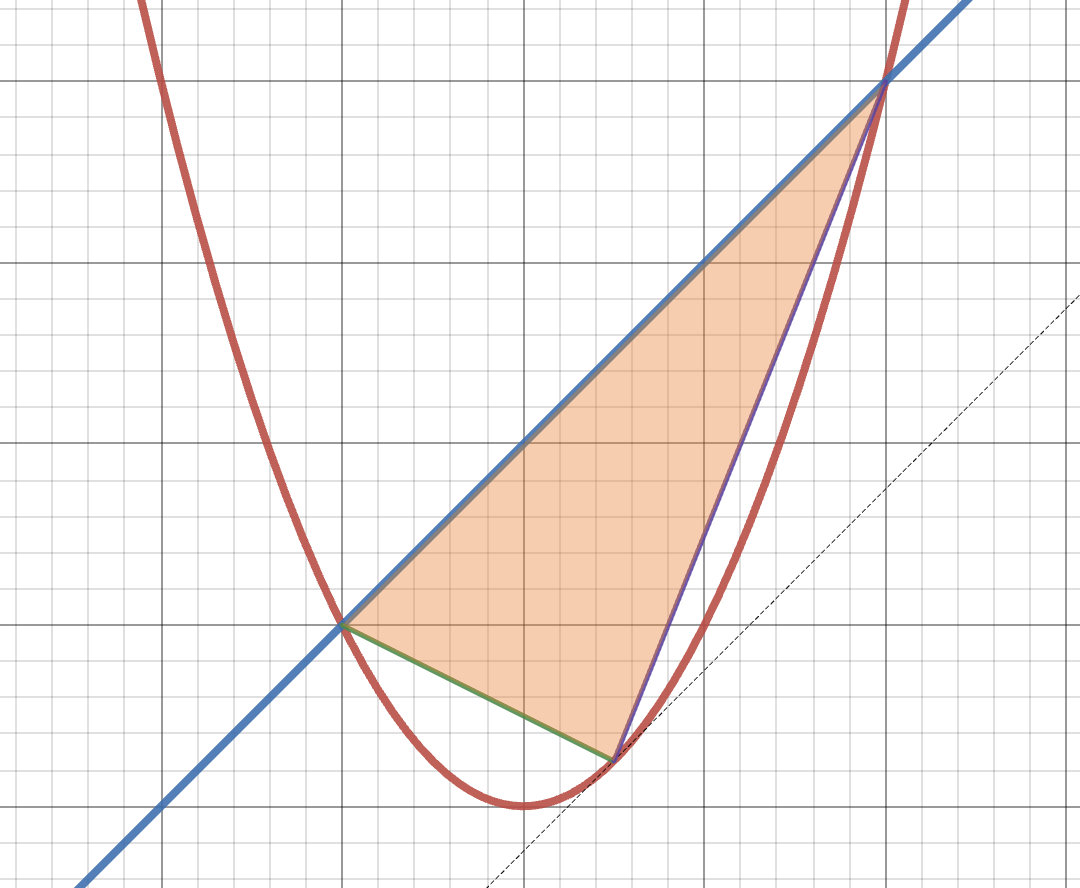
Exercise 35
- Write down a formula for the area of the triangle whose third vertex lies at
Hint: instead of finding the height of the triangle to use
- Use Calculus I to find the point
This gives us the starting point: the area for which archimedes wishes to compare the parabolic segment. Next - we need to find the parabolic segment’s area. We could of course follow Archimedes’ original method (and if you choose to, this can be your class project!) But here, we will use our modern tools and confirm the answer with calculus:
Exercise 36 Compute the area of the parabolic segment (via integration, as the area between two curves). Show that its exactly
The Area and Circumference Constants
A circle has a circumference constant: the ratio of its radius to its circumference, which we’ve named
It was Archimedes who first showed that these two constants were intimately related, by finding that
Tau is the circumference of the unit circle
And then compute its arclength via the integral
But we can also write down the area of the circle as an integral: the top half of the circle is
Your goal in this problem is to show these two integrals are equal to one another!
Exercise 37 Prove that
Hint: Do
Rewrite the area integrand
Now we just have to evaluate this new integral: Do the
Now just assemble the pieces! You never completed a single integral, but you still managed to prove that
Problem Set VII
Trigonometric Identities:
The following exercise has you compute with some trigonometric identities, which we needed to find the volume of spheres:
Exercise 38 (Integrating
Use this to derive an identity relating
by writing
This result was crucial to our calculation of the volume of the four dimensional sphere in class, where we showed (via a trigonometric substitution)
Using this result gave us the final answer:
The 5-Dimensional Sphere
The unit sphere in five dimensions is given by the set of points
Exercise 39 Calculate the volume of this space by slicing along the
(This will not need any trigonometric substitution) Once you have this, find the “surface area” of this 5-dimensional sphere by differentiation.
High Dimensional Spheres and Cylinders
Exercise 40 The discovery Archimedes was most proud of was that the surface area of the sphere in 3-dimensions was the same as the area of the smallest cylinder surrounding it.
Is the same true in four dimensions? (A four-dimensional cylinder has a sphere’s surface as its “base”, just like a three dimensional cylinder has a circle’s length as its base!)
Problem Set VIII
The Dot Product
One thing we used in our arguments building up the basics of spherical geometry was the fact that the dot product has a nice derivative rule.
Exercise 41 (Product Rule for Dot Product) Let
Our use of the dot product overall is as a tool to give the sphere geometry it defines what we mean by infinitesimal length and by angle. Often we will use this just as a theoretical tool - but its good to get some hands-on practice at the beginning, measuring some actual angles.
Exercise 42 Consider the curves
- Intersect each other at the
- Form a right angle at their point of intersection.
Draw a picture of this situation in 3D on a sphere.
Isometries
Recall the definition of an isometry of
Exercise 43 A permutation matrix is a square matrix where every row and column has exactly one “1”, and the other entries are zero. Prove the following permutation matrix
can be used to define an isometry of
In class we are working our way to prove some facts about isometries, mimicking what we did in the Euclidean plane. In particular, on Tuesday we will prove the following two important facts.
Theorem 1 (The Sphere is Homogeneous) Given any two points
Proposition 3 Let
The first is an analog of translations of the Euclidean plane: we can always find an isometry of the sphere that takes any point to any other. And the second is similar to when we proved that you could build rotations of
Your goal in these next problems is to use these theorems to prove even more: first, prove that you can actually rotate the sphere fixing any point you wish (not just the north pole!)
Exercise 44 Use Proposition prp-sphere-rotate-north-pole and Theorem The Sphere is Homogeneous to show the sphere is isotropic: that given any point
(Hint: first show you can do this when
Next, just like in Euclidean space we often find it useful to combine homogenity and isotropy into one condition: we can move any point and any tangent vector to any other point and tangent vector that we like!
Exercise 45 Let
Hint: Look back at Ex 4 Homework 4!
Problem Set IX
Acceleration
We saw in class that the acceleration of a curve on the unit sphere is the projection of its
Exercise 46 (Geodesic Curvature) The magnitude of the acceleration of a unit speed curve is called its geodesic curvature: its a way to measure how much that curve differs from a geodesic. This exercise, you will calculate the geodesic curvature of the circle of radius
- Let
- Write down a parameterization of
- Find a parameterization of
- What is the acceleration felt on
The idea of measuring acceleration along a surface in
In this next problem, we will get a small taste of what happens in differential geometry, when our space is not nice and symmetric like the plane or the sphere, and we have to resort to finding the geodesic equations and solving them (you won’t have to solve them! Just find them….)
Exercise 47 (Geodesics on Surfaces) Let
Let
- Use calculus to find two tangent vectors to the graph at a point
- Find a normal vector
- Write down the projection of a vector
- Write down the projection of
This is all the data we need to be able to compute acceleration along the surface
- Find
- Find the acceleration of
- What are the geodesic equations for
Curvature
We saw in class that the circumference of a circle of radius
Furthermore, we saw that the area is given by
The idea of curvature is a
Exercise 48 Check this, that as
But
Because the first two limits here are zero, they tell us that the difference between the circumference of a Euclidean circle and a Spherical is very small indeed - they agree to first and second order, and their difference is only revealed at the next (cubic) level.
We use this to define the curvature of any surface, where we normalize things so that the curvature of the unit sphere comes out to be 1:
Definition 4 Let
We dont need to work with circumference however; its possible to measure the curvature of space using area as well!
Exercise 49 Which power
Spheres of Different Sizes
Unlike the Euclidean plane, spheres have no nontrivial similarities: in fact, if you apply a similarity of
Definition 5 (Spherical geometry of Radius
The development of each of these spherical geometries is qualitatively very similar to that for
What changes is the quantitative details: the formulas for length area and curvature. In the next two problems, your job is to redo the calculations that I did for
Exercise 50 (Circumference and area.) What is the formula for the circumference and radius of a circle of radius
Hint: base your circles at
Exercise 51 Using the definition of curvature as a limiting ratio of circumference (Definition def-curvature-surf), compute the curvature of
Problem Set X
Platonic Solids
In these problems we will investigate regular polygons on the sphere. Recall we call a polygon regular if it has rotational symmetries about its center: in particular this implies that all its sides are the same length, and all its angles have the same measure (since isometries preserve both lengths and angles).
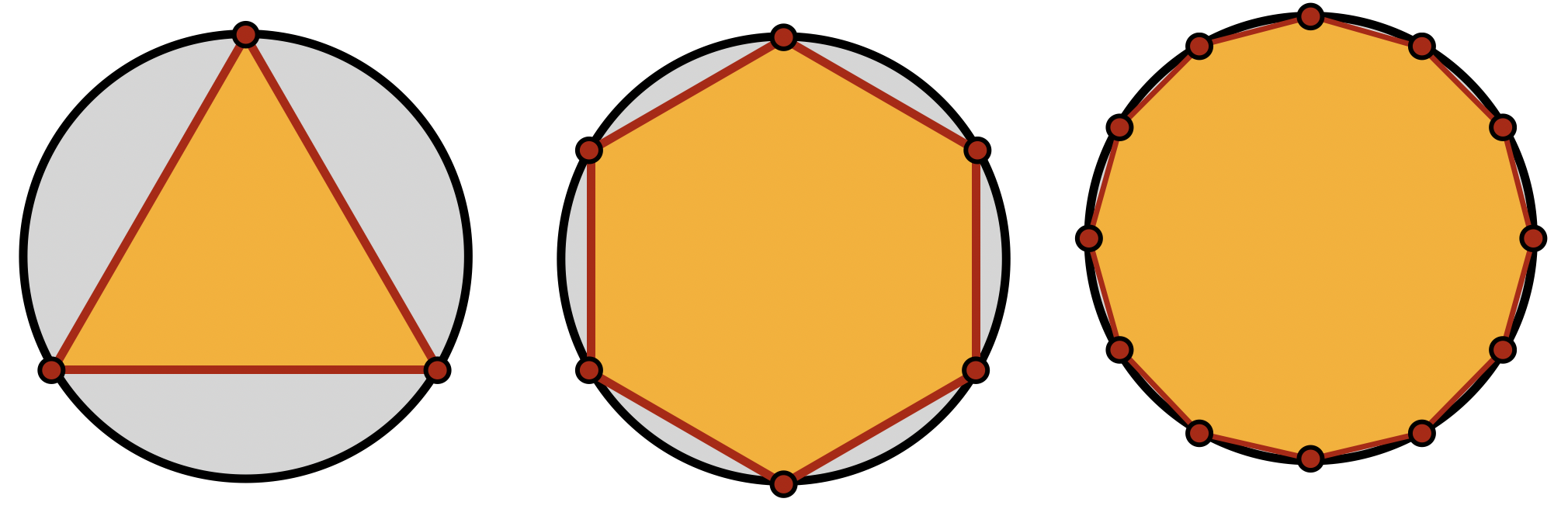
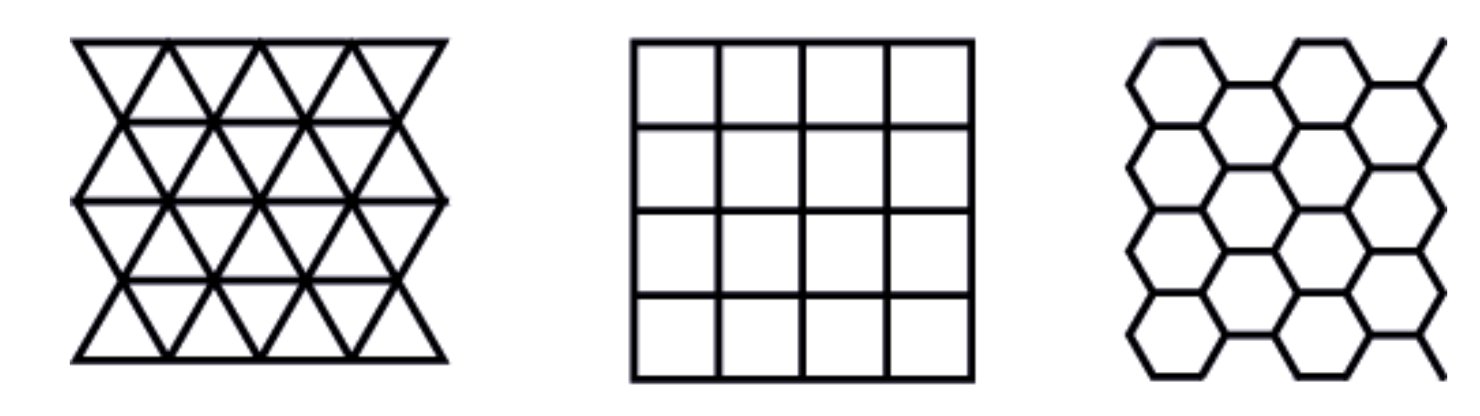
In the Euclidean plane, we know that regular polygons of all side numbers
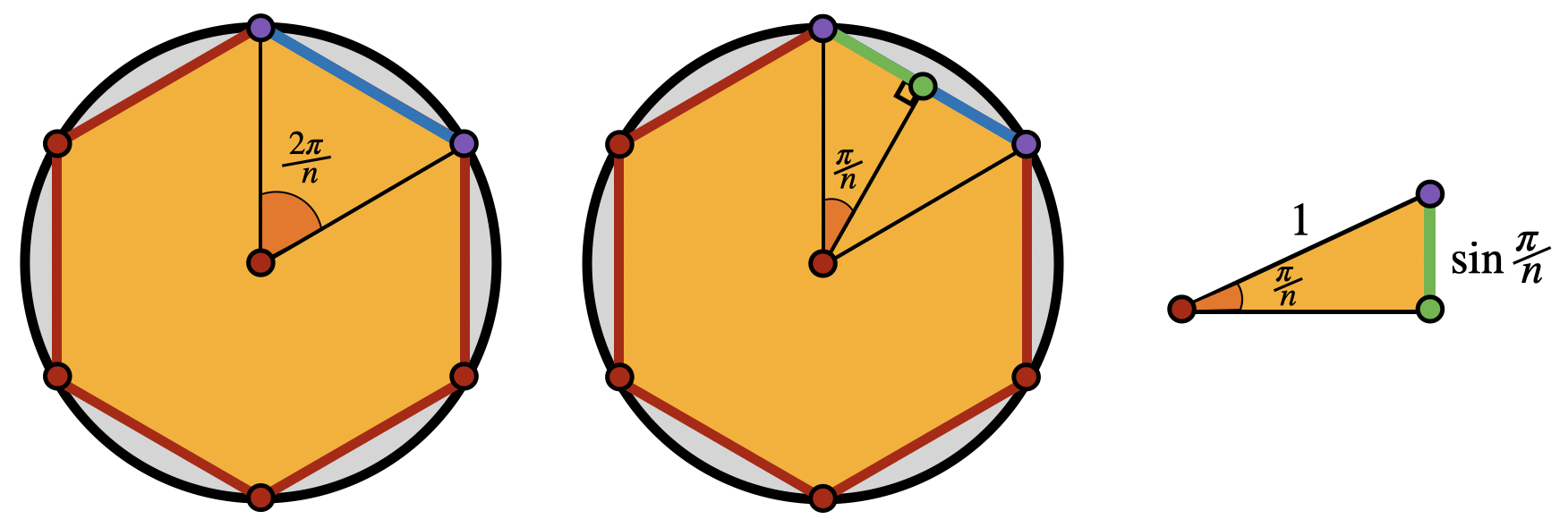
This puts a strong restriction on which regular polygons can be used to tile the plane. To tile the plane, a necessary (but not sufficient) condition is that we need to be able to fit
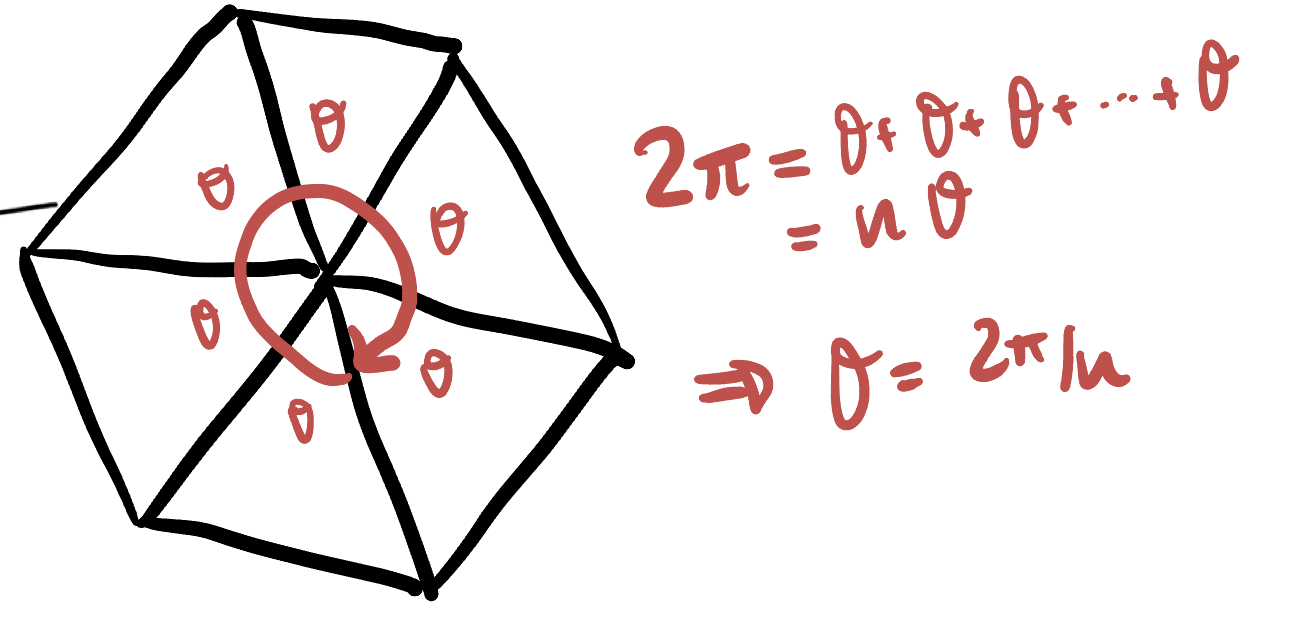
Thus, to figure out which polygons even have a chance of tiling the Euclidean plane, we want to know for which
Thus, we see that its possible to fit six triangles around a vertex, four squares around a vertex and three hexagons around a vertex, but as the angles
This is the start to the classification of regular tilings of the plane, where by what we see from the angle measures, its possible for triangles, squares and hexagons, but impossible for all other shapes!
Our goal here is to investigate what changes on the sphere.
Exercise 52 (Spherical Pentagons)
Find a relationship between the area
Show that there exists a spherical pentagon whose angle evenly divides
What is the area of such a spherical pentagon? How many of these pentagons does it take to cover the entire sphere?
For the pentagon, there was only one possibility, as the restriction that the angle at a vertex be
Exercise 53 (Spherical Triangles) There are three different equilateral triangles that can be used to tile the sphere. Find them! For each triangle:
- How many fit around each vertex?
- How many are needed to cover the sphere?
- What platonic solid does this correspond to?
The Pythagorean Theorem
The fundamental formula in Euclidean trigonometry is the Pythagorean theorem which allows us to measure the length of the hypotenuse of a right triangle in terms of the other side lengths.
The goal of this exercise is to derive the spherical counterpart to this:
Theorem 2 (Spherical Pythagorean Theorem) Given a right triangle on
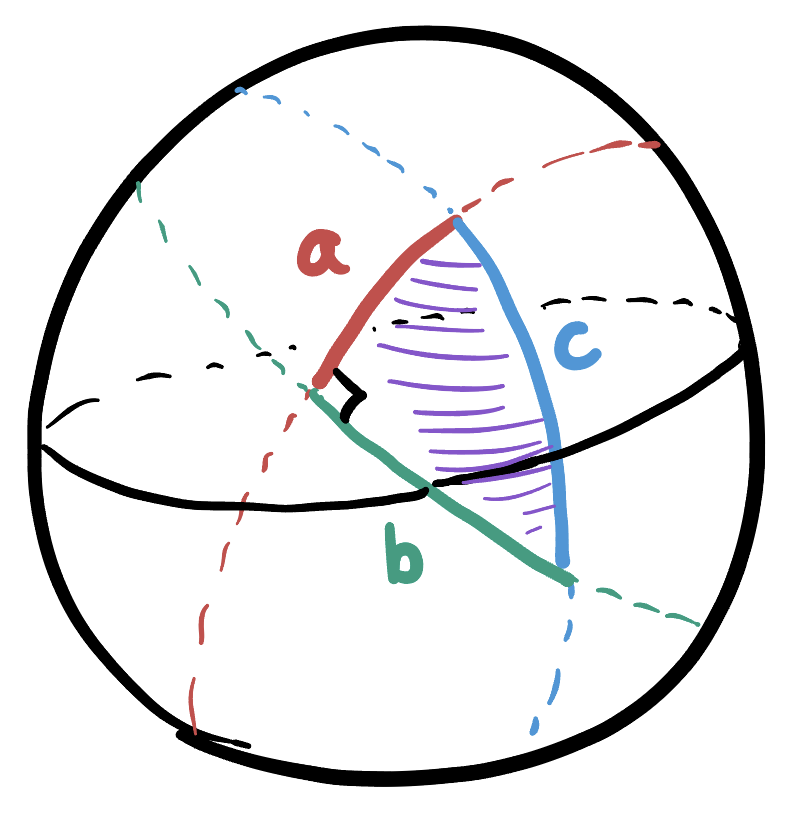
Exercise 54 (Deriving The Pythagorean Theorem) Prove that the formula given above really does hold for the legs and hypotenuse of a right triangle on
Hint: move your triangle so the right angle is at the north pole, and the legs are along the great circles on the
On a sphere of radius
Its often more useful to rewrite this result in terms of the curvature
Theorem 3 (Pythagorean Theroem of Curvature
As a sphere gets larger and larger in radius, it better approximates the Euclidean plane. We might even want to say something like in the limit
Exercise 55 (Euclidean Geometry as the Limit of Shrinking Curvature) Consider a triangle with side lengths
Compute the Taylor series of both sides of
in the limit
Trigonometry
Following the derivation of the spherical pythagorean theorem, we might next hope to discover relationships between the sides of a spherical right triangle and its angle measures. And, indeed we can!
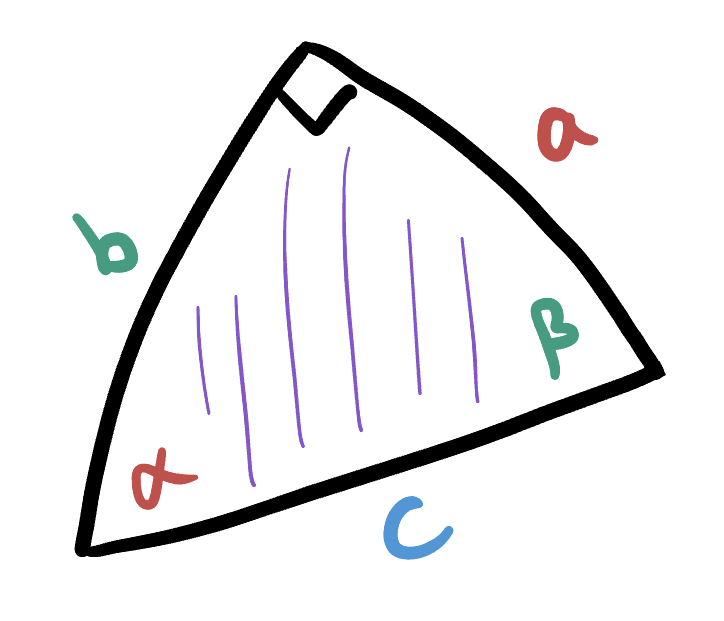
The corresponding laws of spherical trigonometry are as follows:
Theorem 4 (Spherical Trigonometric Relations) For a right triangle with angles
You will not be responsible for the derivation of these formulas, nor for remembering them: if you ever need them they will be given to you!
One of the most biggest differences between spherical trigonometry and its Euclidean counterpart is that its possible to derive formulas for the length of a triangles’ sides in terms of only the angle information! This is impossible in Euclidean space because of the existence of similarities: there are plenty of pairs of triangles that have all the same angles but wildly different side lengths! No so in the geometry of the sphere.
Exercise 56 Using the trigonometric identities in Theorem Spherical Trigonometric Relations together with the spherical pythagorean theorem Theorem Spherical Pythagorean Theorem, show that the side length
Hint: start with the formula for
Formulas such as this are incredibly useful for calculating the side lengths of polygons, by dividing them into triangles and using facts that are known about their angles.
Exercise 57 (Spherical Trigonometry) Use spherical trigonometry to figure out the side lengths of the pentagon you discovered in the first exercise.
Hint: can you further divide the five triangles you used before, into ten right triangles inside the pentagon?
Problem Set XI
Orthographic Map
Exercise 58 Can you find the coordinates
Hint: can you make the problem easier for yourself by restricting
You can see how this would make such a map difficult to use for navigation: it would look like the map is telling you to turn
Because having to do computations like these constantly when working with a map is a huge technical headache, mathematicians much prefer conformal maps, where the angle you see in the Euclidean plane accurately represents the map-angle, and all of this is unnecessary. (This is why the main map employed by mathematicians, Stereographic Projection, is conformal).
Archimedes Map
Read the section of the textbook on Archimedes Map (in the Examples chapter). Give a proof that this mao is infinitesimal area preserving following the outline below:
Exercise 59
- Show that at each point
- Find their lengths on the sphere (ie the map-lengths), and use this data to find the area of the infinitesimal rectangle they form.
- Observe that everything beautifully cancels and the area is still one, even though the square was stretched into a rectangle!
Since the infinitesimal area is unchanged by the map at each point, we can finish Archimedes proof via integration (which I do below, using your exercise)
Theorem 5 The surface area of the unit sphere is the same as that of its Archimedes map: that is, the same as the area of its bounding cylinder.
Proof. Archimedes map captures every point of the sphere except the north and south poles. Since points have zero area, this omission has no effect on our actual question so we can proceed to calculate with the map
But now we know that
Stereographic Projection:
Read the stereographic projection section first (we will cover the necessary bits in class as well)
The stereographic projection map has many uses in mathematics beyond just representing points of the sphere on the plane. Because it is conformal (angle preserving), its often used as a tool to help build more interesting conformal maps between regions of the plane, following this general recipe:
- Start with a region on the plane.
- Use
- Do something to the sphere, moving the region around
- Use
The overall composition is a map between two regions on the plane, that was created by going to the sphere and back! In these exercises, we will deal with a fundamental example of this, and construct a map from the unit disk onto half of the entire plane!
The strategy above is summarized for this case in the following three figures:
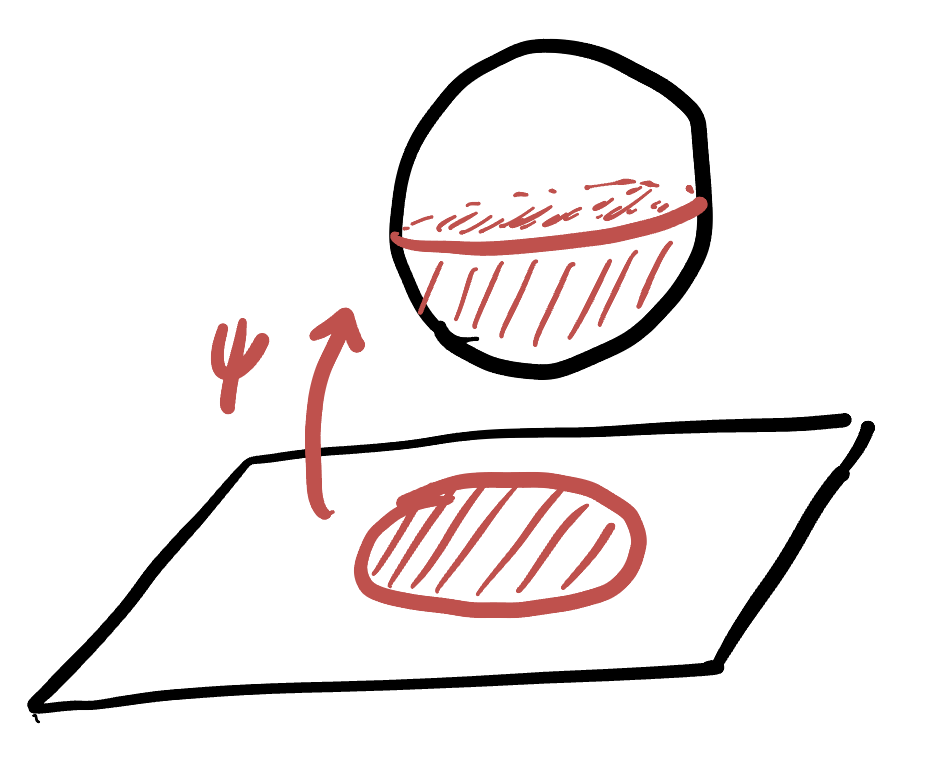
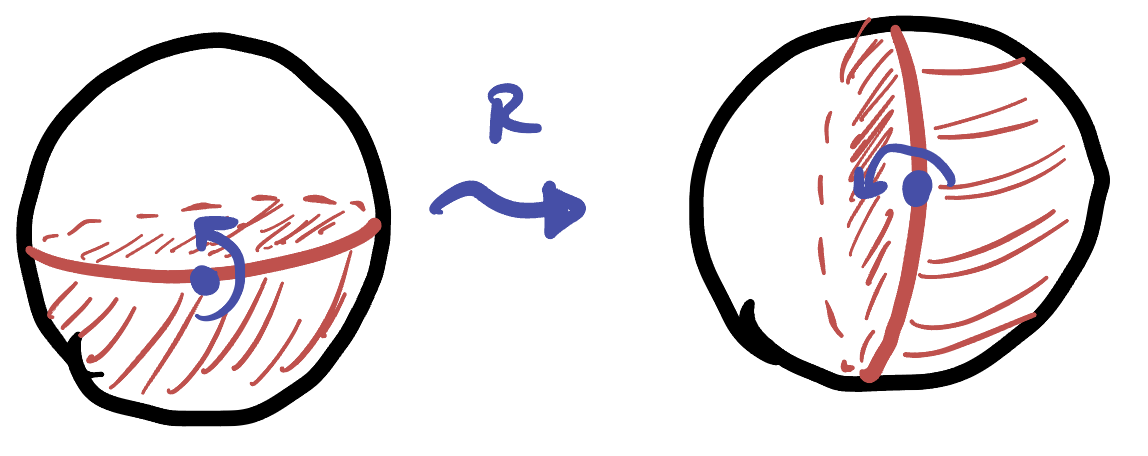
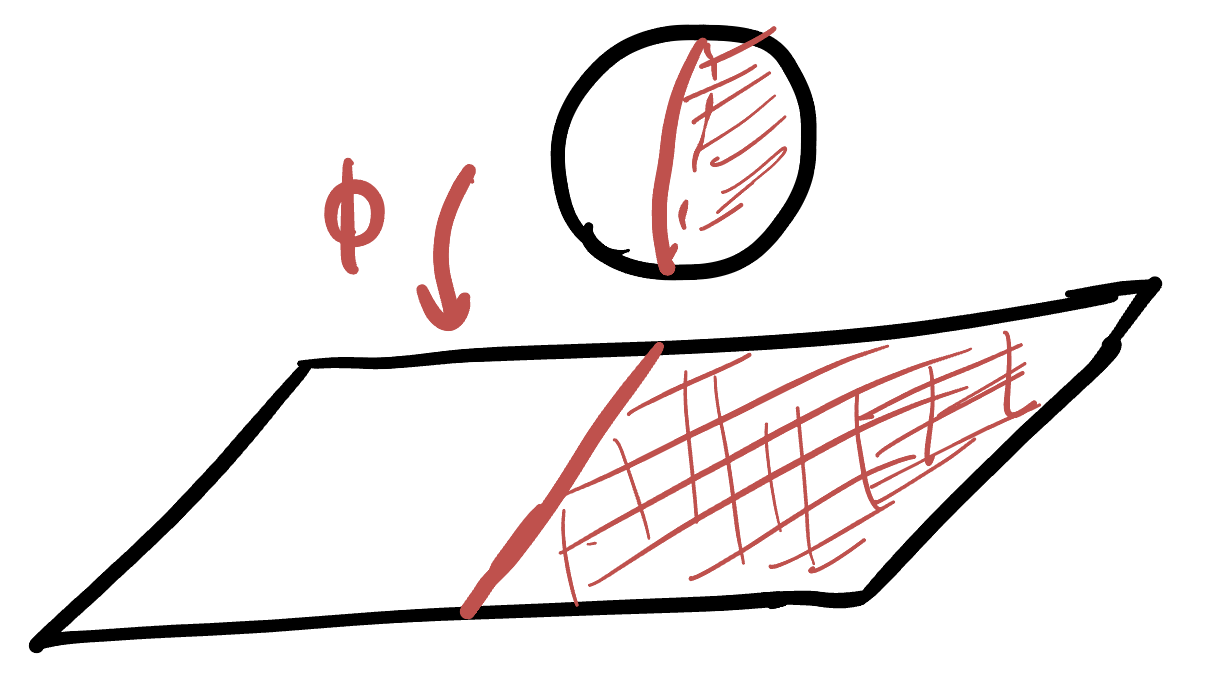
Exercise 60 (Disk and Half Plane: Construction) Let
By building it step by step:
- Start with
- Apply
- Rotate the sphere about the
- Apply
This map is conformal - meaning that it preserves all angles! And even more than that, it takes generalized circles to generalized circles.
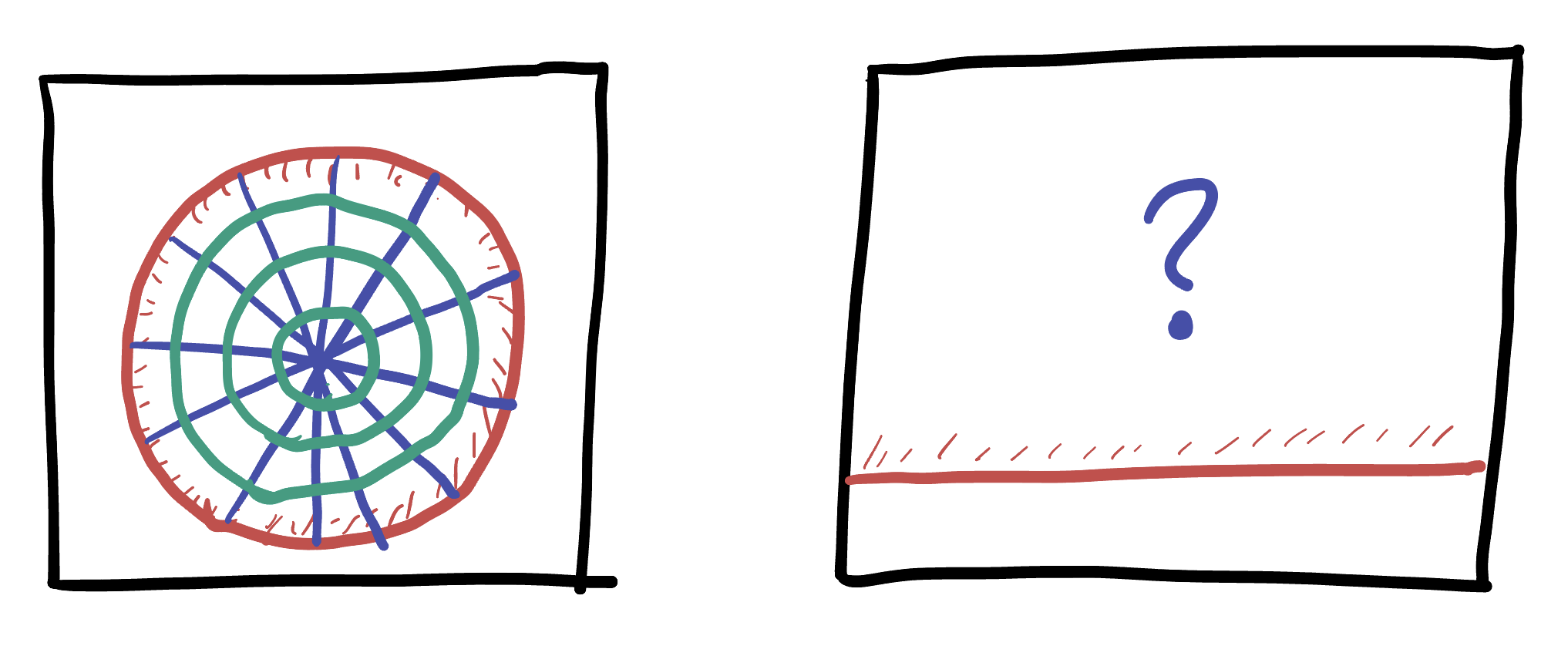
Exercise 61 (Disk and Half Plane: Understanding) Prove that these claims are in fact true: that our new function is conformal, and sends generalized circles to generalized circles. Hint: what kinds of maps is it built out of? What do each of these maps to do angles, or to generalized circles (on the plane) / circles (on the sphere)?
Use this to “transfer” this picture of polar coordinates in the unit disk onto the plane, via our new map.
Spheres of Radius
The chapter on stereographic projection deals with the unit sphere. It is not too hard to generalize what we have done to spheres of other radii, and while this may not sound super exciting at first, it actually turns out to be absolutely fundamental to how we are going to discover hyperbolic space! So, it is a rather important exercise to work this all out for yourself.
The good news is you have this entire chapter as a guide, where I’ve worked out many of the details for the case of the unit sphere. The formulas will be quite similar, but there’ll be
Definition 6 Let
Exercise 62 Show that the formulas for both the chart and the parameterization of stereographic projection here are as follows:
(It might help to look back at Proposition Stereographic Projection Formula, and attempt Exercise exr-stereo-parameterization).
Running through the same arguments as in the chapter above (which you don’t have to write down), its straightforward to check that this new map is a conformal map between
Exercise 63 At a point
Once you know this, follow the argument style of Theorem Stereographic Dot Product to compute the map-dot product on the plane, and show that it is equal to
Problem Set XII
Getting Used to Hyperbolic Space
Exercise 64 (Hyperbolic Circle Area) In this exercise you will go through the transition-style arguments we use to turn formulas on the sphere into their analogs in hyperbolic geometry, much like we did in class.
The starting point is the formula for the area of a circle of radius
- Re-express this in terms of curvature
- Convert to the Taylor series
- Plug in
- Convert back to hyperbolic trigonometric functions
What is the correct hyperbolic formula? (We wrote it down without doing the full derivation in class, so you can confirm)
Exercise 65 (Hyperbolic Pizza) One way to try and develop intuition for the strange behavior of circles is to think about the type of circles we see in daily life: pizzas! One major factor determining how good a pizza is is its crust percentage which we will define as
In this probelm we will consider pizzas which have 1 inch crusts: meaning a 10 inch (radius) pizza has a 9inch radius center of toppings, surrounded by a 1 inch thick circle of crust.
- Show the CrustPercent for Euclidean pizza is
- What is the CrustPercent for a hyperbolic pizza of radius
Exercise 66 (Hyperbolic Pizza II) In this problem, we will imagine our unit to be inches (so, the radius appearing in formulas for space of curvature
You are at a pizzerias and are trying to decide if the 5 inch radius pizza they sell is large enough for you and your friends. They also sell a six inch (radius) pizza, but it costs twice as much. At first, you think this sounds crazy! But is this actually a good deal, or not?
Your friend is feeling very hungry, and jokingly asks the pizza-maker how large of a pizza he would need to order so that its areas is the same as an american football field (
Hint: invert the formula for area in terms of radius, to get radius in terms of area, then plug into a calculator!
Working with the Models
Exercise 67 (Hyperbolic space is homogeneous) We proved in class that the horizontal translations
Combining these two, prove that
Hint: can you first show that you can build an isometry that takes
Exercise 68 (The Circumference of Circles) In the Disk Model, if
Using these two, prove that
Together these two arguments prove that the geometry modeled by the Half Plane and the Disk has the circumference function