16 \(\pi\)
One of the great mysteries of mathematics is the ubiquity of certain particular numbers. It scarcely matters what field of mathematics you are working in, if you think hard enough and dig deep enoughs you’ll inevitably run into the mysterious number \[2.718281828459\ldots\]
apearing in your calculations. (This will even happen to us, in this class, not too far from now!) This number appears in everything from finance to probability, to differential equations, group theory, real analysis, and non-euclidean geometry. But this is not even the craziest of the numerical conspiracies: the true king of almost magically ubiquitous numbers is \[3.141592653589\ldots\]
We have already met this number in this class, but our brief encounter (as the area of the unit circle) does not provide much evidence or intution for why this should appear everywhere in mathematics! That is the goal of this chapter: we will see that a collection of rather remarkable properties of Euclidean space make it so that many conceptually-different mathematical quantities are all (1) constant and (2) have values directly related to \(\pi\). Its easiest to explain all of this via examples, so instead of further discussion let’s just dive right in.
16.1 Circle Constants
16.1.1 The Length Constant
For any circle \(C\) in the plane we can define its length factor to be the ratio of its circumference to its radius: that is, how many times do we need to lay out the radius to equal the circumference? If we write \(\mathrm{circ}(C)\) to denote the circumference, or arclength of the circle \(C\) and \(\mathrm{rad}(C)\) to denote the radius, the quantity we are interested in here is just their ratio:
\[\tau(C)=\frac{\mathrm{circ}(C)}{\mathrm{rad}(C)}\]
If we write \(C_{p,r}\) for the circle centered at \(p\in\EE^2\) of radius \(r\), we alternatively could express this length ratio as
\[\tau(C_{p,r})=\frac{\length(C_{p,r})}{r}\]

We use the letter \(\tau\) for this ratio as its value for the unit circle is \(\tau\) as we have defined it previously: \[\tau := \tau(C_{O,1})=\length(C_{O,1})\]
Both the numerator and denominator of this definition depend on the circle \(C\) being considered - so there’s no a priori reason to assume that this ratio should be independent of the choice of circle. Indeed - we will see very shortly in both spherical and hyperbolic geometry the analog of \(\tau(C)\) takes different values for different circles!
But, as an incredible consequence of the existence of isometries and similarities of the Euclidean plane, it turns out that here this number is a constant!
Theorem 16.1 (Length Factor is Constant) The ratio of a circles circumference to its radius is a constant, independent of the circle.
Proof. Let \(C_{p,r}\) be any circle in the plane - centered at some point \(p\) and of some radius \(r\). Now let \(T\) be the translation which takes \(p\) to the origin \(O\). Isometries preserve distances, and thus send circles to circles. This means \(T(C_{p,r})\) is a circle of radius \(r\) (a distance) centered at \(O\): in symbols \[T(C_{p,r})=C_{O,r}\]
Isometries also do not change the lengths of curves (Theorem 11.2), so we know that \(\len(C_{p,r})=\len(C_{O,r})\). And since it doesnt change distances (like the radius: Proposition 12.3) we see that \(C_{p,r}\) and \(C_{O,r}\) have the same length ratios: \[\tau(C_{p,r})=\frac{\len(C_{p,r})}{r}=\frac{\len(C_{O,r})}{r}=\tau(C_{O,r})\]
Now we will show that \(C_{O,r}\) has the same length factor as the unit circle, and thus our original circle had the same length factor as the unit circle! To do so, we use the similarity \(\sigma(x,y)=(Rx,Ry)\). This has scaling factor \(r\), and so scales all lengths of curves (Proposition 11.3), and all distances (Exercise 12.4) by \(r\). Thus, \(\sigma\) takes the unit circle \(C_{O,1}\) to the circle \(C_{O,r}\) and also takes \(\len(C_{O,1})\) to \(r\len(C_{O,1})\). Because both the circumference of the circle and the radius got scaled by \(r\) the length factor is unchanged:
\[\tau(C_{O,1})=\frac{\len(C_{O,1})}{1}=\frac{r\len(C_{0,1})}{r}=\frac{\len(C_{O,r})}{r}=\tau(C_{O,r})\]
Stringing all the equalities together, we see \[\tau(C_{p,r})=\tau(C_{O,r})=\tau(C_{O,1})\]
Thus every circle has the same length factor as the unit circle, so the length factor is constant.
Definition 16.1 (The Circle Length Constant) The constant ratio of the circumference to the radius of a circle to its radius is \[\tau = \frac{\length(C_{p,r})}{r}\] In Exercise 3 we found a good approximation to this following the method of archimedes: \[\tau\cong 96\cdot 2\cdot \sqrt{2- \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}}\approx 6.282904\ldots\]
Thus in any mathematical problem involving a circle’s length, the number \(\tau(C)=\tau = 6.28\ldots\) is bound to show up: this is just the circumference measured in units of radii!
16.1.2 The Area Constant
We’ve found that similarites force the length factor of circles to be a constant - and this explains at least some occurences of a geometric constant appearing in mathematics. But lengths aren’t the only important quantity related to circles out there! It’s equally natural to consider their area.
Here it doesn’t make sense to measure a circles area in units of radii, since radii are a length and area is….not a length. Instead its more natural to measure area in units of radii squared: how many squares with side length the radius does it take to fill up a circle? For a given circle \(C\), we will call this area factor \(\pi(C)\):
\[\pi(C_{p,r})=\frac{\mathrm{Area}(C_{p,r})}{r^2}\]

We use the letter \(\pi\) for this as we have already defined \(\pi\) to be this ratio for the unit circle \(C_{O,1}\):
\[\pi := \pi(C_{O,1})=\mathrm{area}(C_{O,1})\]
Again, this fraction involves quantities related to the particular circle \(C_{p,r}\) in both the numerator and denominator, so its totally conceivable that its value would depend on the particular circle being considered! (And, in spherical and hyperbolic geometry, it will).
But perhaps after seeing the crucial role of similarities in the argument for the constancy of \(\tau\), perhaps you already have a sneaking suspicion that the analogous trick will prove \(\pi\) to be constant here.
Theorem 16.2 (Area Factor is Constant) The ratio of a circle’s area to its radius squared is constant, independent of the circle
Proof. The proof here is nearly identical to the length factor case, except we need to use the fact that similarites scale area by the square of their similarity factor (Theorem 15.3), instead of the fact that they linearly scale length.
Again since isometries don’t change distances or areas we can move an arbitrary circle \(C_{p,r}\) to the origin, \(C_{O,r}\) and know that \[\pi(C_{p,r})=\pi(C_{O,r})\]
Next we see that \(\pi(C_{O,r})\) is the same as the area factor of the unit circle, using the similarity \(\sigma(x,y)=(rx,ry)\), which sends \(C_{O,1}\) to \(C_{O,r}\) and \(\mathrm{area}(C_{O,1})\) to \(r^2\mathrm{area}(C_{O,1})\).
\[\pi(C_{O,1})=\frac{\mathrm{area}(C_{O,1})}{1}=\frac{r^2\mathrm{area}(C_{0,1})}{r^2}=\frac{\mathrm{area}(C_{O,r})}{r^2}=\pi(C_{O,r})\]
Stringing these together we see that every circle’s area ratio is the same!
\[\pi(C_{p,r})=\pi(C_{O,r})=\pi(C_{O,1})\]
Definition 16.2 For any circle \(C\) in the Euclidean plane, the ratio of its area to squared radius is a constant denoted by \[\pi=\frac{\mathrm{Area}(C_{p,r})}{r^2}\]
This tells us that we should expect yet another constant to be popping up throughout mathematics: anytime a discussion of circles and their areas show up, we will run into \(\pi\) as the natural conversion factor from radius squared to area!
Archimedes could have went on to estimate the value of \(\pi\) by calculating the area of an inscribed polygon or circumscribed polygon, by adding up the area of triangles.
Exercise 16.1 (\(\pi\) via inscribed areas.) The area of a triangle is half its base times it’s height. Can you calculate the area of a polygon that circumscribes the circle to get an approximation of \(\pi\)? Try starting with a hexagon. Then, can you find a way to use trigonometric identities to double the number of sides repeatedly, like we did for circumference?
However, Archimedes did not do this…he did something much more clever.
16.1.3 Equality
Alone these two facts don’t point towards a single, unified constnat showing up in mathematics, rather they suggest we should be seeing two different values, \(\pi\) and \(\tau\), in two different circumstances: area and length respectively.
It was already known to Euclid that these two constants exist: in CITE PROP Euclid shows the circumference of a circle is always proportional to its radius, and in CITE PROP he shows the area is always proportional to the radius squared. But it wasn’t until the work of Archimedes that we discovered the truly astounding fact that these two constants are related to one another! Recall the main result of the measurement of the circle
Theorem 16.3 The area of a circle is equal to that of a triangle whose base is the circle’s circumference, and whose height is the circles radius.

Because we know the area of a triangle to be half its base times its height, this tells us that
\[\pi r^2 = \frac{1}{2}(\tau r)(r)\]
Or, cancelling the factors of \(r\) and re-arranging,
\[\tau = 2\pi\]
That is, the two circle constants are just integer multiples of one another! This means whether we are interested in lengths or areas, so long as we are doing mathematics that invovles a circle this constant is going to appear. (This also explains why you see so many formulas with a \(2\pi\) in them: this is really the length constant \(\tau\)! But since they are rationally related we’ve just chosen one of them, \(\pi\) to write everything in terms of.)
As we have been doing throughout this section of the book, a good exercise is to prove archimedes observation using modern techiques. We will give two approaches here, one based on integration, and another on differentiation.
16.1.3.1 Integration
Both lengths and areas in our modern version of geometry are calculated via integrals, so it’s no surprise that the values of \(\pi\) and \(\tau\) themselves are integrals. Indeed, as we saw in Corollary 14.2 we can write the circumference of the unit circle as
\[\tau = \int_{-1}^1 \frac{2}{\sqrt{1-t^2}}dt\]
And, from the area chapter (Corollary 15.1) we saw we can express its area as
\[\pi = \int_{-1}^1 2\sqrt{1-x^2}dx\]
In this homework excercise we will use familiar calculus techniques (just u-substitution!) to relate these integrals to one another (without evaluating either!) giving a modern proof of Archimedes’ theorem.
Exercise 16.2 Prove that \[\int_{-1}^1\frac{1}{\sqrt{1-t^2}}dt=\int_{-1}^1 2\sqrt{1-x^2}dx\] Thus showing thtat \(\frac{\tau}{2}=\pi\).
Hint: Do \(u\)-substitutions to the integrals to make them into the same integral. The goal isn’t to evaluate them and get a number! This is just a Calc II problem - but a tricky one, so here’s one outline you could follow:
Rewrite the area integrand \(\sqrt{1-x^2}\) as \(\frac{1-x^2}{\sqrt{1-x^2}}\). Use properties of integrals to break this into two integrals, and see \[\pi = \tau -\int_{-1}^1\frac{2x^2}{\sqrt{1-x^2}}dx\]
Now we just have to evaluate this new integral: Do the \(u\)-substitution \(u=\sqrt{1-x^2}\) to this, to show that \[\int_{-1}^1 \frac{2x^2}{\sqrt{1-x^2}}dx=\int_{-1}^1 2\sqrt{1-u^2}du=\pi\] (This \(u\)-sub requires some work: you’ll need at some point to solve for \(x\) in terms of \(u\)!)
Now just assemble the pieces! You never completed a single integral, but you still managed to prove that \(\tau =2\pi\).
16.1.3.2 Differentiation
To give a third proof of this fundamental equality, we will start wtih the formula defining the area of a circle of radius \(r\):
\[\mathrm{area}(C_{p,r})=\pi r^2\]
Let’s think a bit about the derivative of this function: this is easy to compute by hand \[\frac{d}{dr}\mathrm{area}(C_{p,r})=\frac{d}{dr}\pi r^2=2\pi r \]
but what does it mean? For this, we need to return all the way to the fundamentals, and think about the definition of the derivative. To unclutter the notation, below I am going to write \(\mathrm{area}(r)\) for the area of a circle of radius \(r\) (the area doesn’t depend on the center point after all!)
\[\frac{d}{dr}\mathrm{area}(r)=\frac{\mathrm{area}(r+h)-\mathrm{area}(r)}{h}\]
The numerator here is a difference of areas - between the area of a disk with radius \(r+h\) and a disk of radius \(r\). This is what you get if you remove a disk of radius \(r\) from a disk of radius \(r+h\), so this is the area of a thin circular ring.
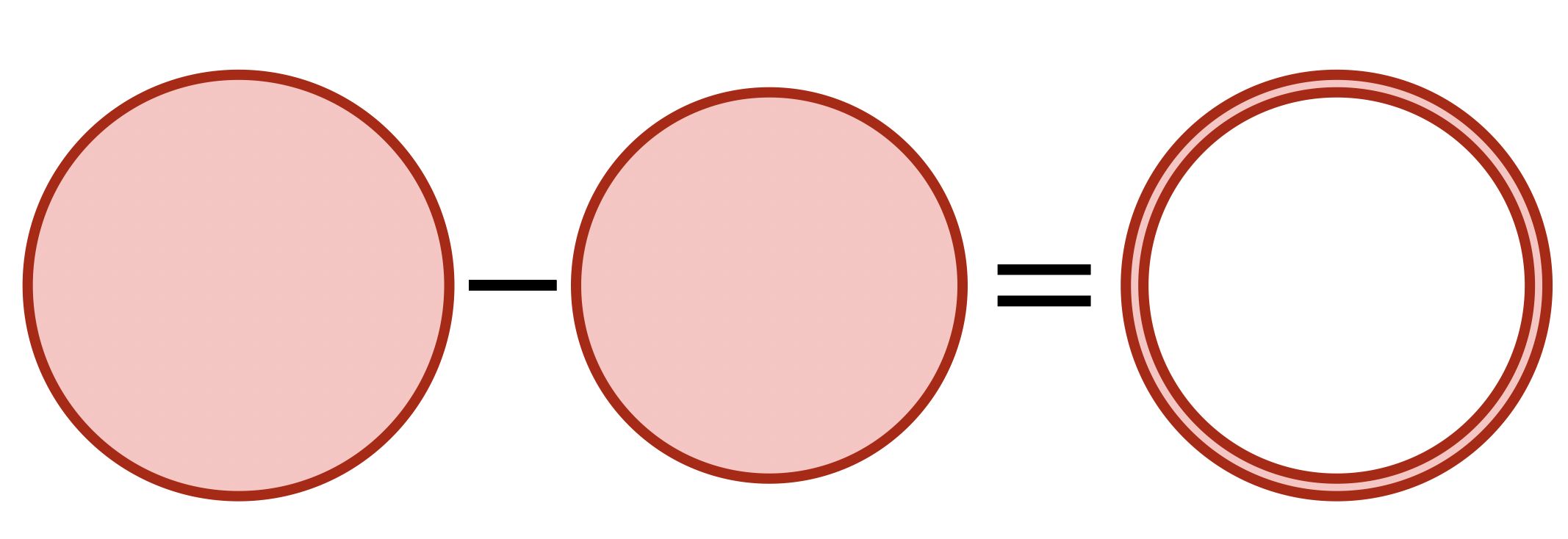
What’s the area of this ring? In the limit as \(h\) becomes infinitesimally small (as we take the limit to become the actual derivative) we can calculate infinitesimally: imagine the circular ring is made of a bunch of tiny squares, whose height is \(h\): since their other sides fit together to form the circumference, the sum of their bases is \(\tau r\). Thus,
\[\mathrm{area}(r+h)-\mathrm{area}(r)\approx(\tau r)h\]
With this approximation becoming exact as \(h\to 0\). But in the derivatrive we divide by h, and are left with just \(\tau r\)!
\[\frac{d}{dr}\mathrm{area}(r)=\tau r=\mathrm{circ}(r)\]
This is an incredibly cool fact: so we should box it off as a theorem for future reference!
Theorem 16.4 The derivative of the area function for circles of radius \(r\) is the circumference function \[\frac{d}{dr}\mathrm{area}(r)=\mathrm{circ}(r)\]
But now we are all but complete with our third way of proving \(\tau=2\pi\). We know the area function is \(\mathrm{area}(r)=\pi r^2\), and so we can take its derivative to get \(2\pi r\). Similarly, we know the circumference formula is \(\tau r\), so this relathionship simplifies to
\[2\pi r = \tau r\]
And, canceling the \(r\) (or evaluating at the unit circle, \(r=1\)) gives the result!
16.1.4 Trigonometric Substitution
The intimate relationship between \(\tau\) and \(\pi\) is so fundamental that I cannot help but offer yet another proof of this result. This may seem wasteful but is in fact often a useful thing to do in mathematics - as different proofs generalize to different situations easier.
Here, we will focus directly on the area integral of Corollary 15.1,
\[\pi=\int_{-1}^1 2\sqrt{1-x^2}dx\]
and try to directly evaluate it via the fundamental theorem of calculus (finding an antiderivative, and plugging in the endpoints). To do a little pre-emptive simplifcation, we may notice that the integrand is an even function of \(x\) so we may instead choose to integrate on half the domain, say \([0,1]\), and double the result:
\[\pi = 4\int_0^1 \sqrt{1-x^2}dx\]
Now, we perform a rather clever substitution to the integral. Because we rigorously studied the trigonometric functions we recall that \(\cos^2\theta +\sin^2\theta = 1\), and thus if \(x=\sin\theta\) we could simplify \(1-x^2\) as
\[1-x^2=1-\sin^2\theta = \cos^2\theta\]
Thus, \(\sqrt{1-x^2}\) simply becomes \(|\cos\theta|\). And, because we computed the derivative of \(\sin\theta\) and \(\cos\theta\) in the chapter on angles, we know that
\[dx=d(\sin\theta)=\cos\theta d\theta\]
The last portion of the integral we need to convert are the bounds. The lower bound of \(x=0\) means we seek \(\theta\) with \(x=\sin\theta = 0\). From our defintion of \(\sin\) and \(\cos\), we see this happens at \(\theta=0\) since \(\sin\) is the \(y\) coordinate, and \(\theta=0\) corresponds to the starting point \((1,0)\). Next, for the top bound \(x=1\) we seek the \(\theta\) value with \(x=\sin\theta =1\). This occurs along the positive \(y\) axis, so a quarter turn around the circle, or \(\theta = \tau/4\). Putting all these pieces together, we see
\[\int_0^1 \sqrt{1-x^2}dx=\int_0^{\frac{\tau}{4}}|\cos\theta|\cos\theta d\theta =\int_0^{\frac{\tau}{4}}\cos^2\theta\, d\theta\]
It appears we aren’t doing much better: we didn’t know the antiderivative of \(\sqrt{1-x^2}\) which is what set all of this off, but we also don’t know the antiderivative of \(\cos^2\theta\)! However, the reason this type of substitution is powerful is that there arent many square root identities out there we can use to change how a function is represented, but there are plenty of trigonometric identities.
Indeed, from the angle sum identity we derived, \[\cos(a+b)=\cos a\cos b-\sin a\sin b\]
by setting \(a=b=\theta\) and using the pythagorean identity \(\cos^2\theta+\sin^2\theta=1\), one can show that
\[\cos^2\theta = \frac{1+\cos 2\theta}{2}\]
Exercise 16.3 Derive this identity.
This lets us rewrite our integral
\[\int_0^{\frac\tau 4}\cos^2\theta\,d\theta = \int_0^{\frac\tau 4}\frac{1+\cos2\theta}{2}d\theta =\frac{1}{2} \int_0^{\frac\tau 4}d\theta +\frac{1}{2}\int_0^{\frac\tau 4}\cos 2\theta\,d\theta\]
The first of these integrals is straightforward: its \(\tau/4\). For the second integral, we can \(u\)-sub \(u=2\theta\) to get
\[\int_0^{\frac\tau 4}\cos 2\theta d\theta =\frac{1}{2}\int_0^{\frac\tau 2}\cos u\, du\]
But now - finally - we know the antiderivative! Since the derivative of sine is cosine, we can compute
\[\int_0^{\frac\tau 2} \cos u du =\sin u\,\Bigg|_{0}^{\frac\tau 2}=\sin\left(\frac\tau 2\right)-\sin(0)=0-0=0\]
All that work for zero!! But, putting it all together, we see
\[\int_0^1\sqrt{1-x^2}dx=\int_0^{\frac\tau 4}\cos^2\theta d\theta = \frac{1}{2}\frac\tau 4\]
And going back to the very beginning we recall that \(\pi\) was exactly four times this integral. Thus
\[\pi = 4\frac 12\frac \tau 4=\frac\tau 2\]
Our fourth independent derivation that \(\tau = 2\pi\).
16.2 Sphere Constants
To talk about things in spheres and cylinders rigorously, we neeed to study a bit of 3-dimensional Euclidean geometry. We will return to this in more detail later in the course, but here we only give a slight taste, as it is important to our overall discussion of \(\pi\).
Just as a circle was the set of points a fixed distance (the radius) from a fixed point (the center), a sphere is defined just as a circle except now in three dimenions. We found the equations for distance minimizing curves in 2D to be affine, and that let us find the distance formula \(\mathrm{dist}((x,y),(h,k))=\sqrt{(x-h)^2+(y-k)^2}\) and consequently the fomrula for a circle \((x-h)^2+(y-k)^2=r^2\). All of this carries through with no changes in three dimensions, where the distance formula becomes
\[\dist\left((x,y,z),(h,k,\ell)\right)=\sqrt{(x-h)^2+(y-k)^2+(z-\ell)^2}\]
And consequently, the sphere centered at \((h,k,\ell)\) of radius \(r\) has the formula
\[(x-h)^2+(y-k)^2+(z-\ell)^2=r^2\]
The surface area of the sphere is defined exactly as we have done in the plane, by dividing its surface into infinitesimal parallelograms \(dA\), and then integrating the area of these parallelograms to get the final answer. The volume is defined analogously, except we now need a notion of infinitesimal volume in 3-dimensions. Volume of an infinitesimal 3d rectangle is given by length times width times height, or in symbols \[dV = dxdydz\] and so three dimensional volumes are calculated by three iterated integrals instead of the double iterated integrals for area.
16.2.1 Fundamental Constants
Let \(S_{p,r}\) denote the sphere of radius \(r\) centered at \(p\), just as we did for \(C_{p,r}\) for the circle. Like in two dimensions, we can define an area ratio and a volume ratio for the sphere, comparing each quantity to the relevant power of \(r\).
Theorem 16.5 (Surface Area Ratio is Constant) The ratio \[\frac{\mathrm{area}(S_{p,r})}{r^2}\] is constant, and independent of the sphere considered.
Proof. The proof strategy here is exactly analogous to what we did for the length and area constants of a circle: we prove that every sphere has the same surface area ratio by using isometries and similarities to relate it to the unit sphere. First, we translate \(S_{p,r}\) to the origin, which does not change lengths or areas. Then, we use a similarity to scale the unit sphere to the sphere of radius \(r\). This scales the surface area by \(r^2\) (as similarities scale areas by \(r^2\)) and it scales length by \(r\). Thus
\[\frac{\mathrm{area}(S_{O,1})}{1}=\frac{r^2\mathrm{area}(S_{O,1}}{r^2}=\frac{\mathrm{area}(S_{0,r})}{r^2}=\frac{\mathrm{area}(S_{p,r})}{r^2}\]
Theorem 16.6 (Volume Ratio is Constant) The ratio \[\frac{\mathrm{vol}(S_{p,r})}{r^3}\] is constant, and independent of the sphere considered.
Proof. Run the same proof as above, but now notice that when we scale volume, infinitesimal volume is measured by \(dxdydz\), so if each is scaled by \(r\) we get \[rdxrdyrdz=r^3dxdydz\] Thus volumes are scaled by \(r^3\) under a similarity, and so
\[\frac{\mathrm{vol}(S_{O,1})}{1}=\frac{r^3\mathrm{vol}(S_{O,1}}{r^3}=\frac{\mathrm{vol}(S_{0,r})}{r^3}=\frac{\mathrm{vol}(S_{p,r})}{r^3}\]
Just as we gave names \(\tau\) for the length constant and \(\pi\) for the area constant of circles, we may be tempted to give names to these two new fundamental constants that we just discovered. And, temporarily we will do so, but these names will not stick around for long - we will instead find both to be related to the circle constants! To keep things concise during their breif existence we will name the surface area constant \(C_{Surf}\) and the volume constant \(C_{Vol}\).
16.2.2 Relationship to \(\pi\).
The work Archimedes was most proud of we have barely discussed yet in this class. In his book The Sphere and the Cylinder, Archimedes managed to find a relationship between the formulas for the surface area and volume of a sphere, and relate them to those of a cylinder. This was of course a big deal because the volume of a shape with curved sides had never been caclulated before, but it was an even bigger deal the form that the answer took. Specifically, Archimedes found that for surface area, the area of the sphere is exactly equal to the area of the round side of a the smallest cylinder that can enclose it (whose radius is the same as the spheres, and whose height is the sphere’s diameter)

In modern notation, we would write this relationship with a formula. A cylinder is a rolled up rectangle, and so we can calculate its area with base times height. The base is the circumference of the cylinder (so, \(\tau r\) since this is a circle!) and the height is \(2r\). Thus
\[\mathrm{area}(S_{p,r})= (\tau r )(2 r)=2\tau r^2\]
Because we already proved \(\tau\) is related to \(\pi\) via \(\tau = 2\pi\) we often instead see this written as
\[\mathrm{area}(S_{p,r})=4\pi r^2\]
This tells us immediately the value of the surface area constant, as its definition is just the surface area over \(r^2\)!
Theorem 16.7 (Value of the Surface Area Constant) \[C_{Surf}=\frac{\mathrm{area}(S_{p,r})}{r^2}=4\pi\]
We will prove this using modern tools below, but I’ll postpone the proof until we talk about Archimedes other great discovery - calculating the volume of a sphere.
Through an ingenious argument by slicing, Archimedes showed that the volume of the sphere is the same as the volume of the following complicated sounding shape: the volume in between the cylinder enclosing the sphere (from above), and the double cone that fits inside it:
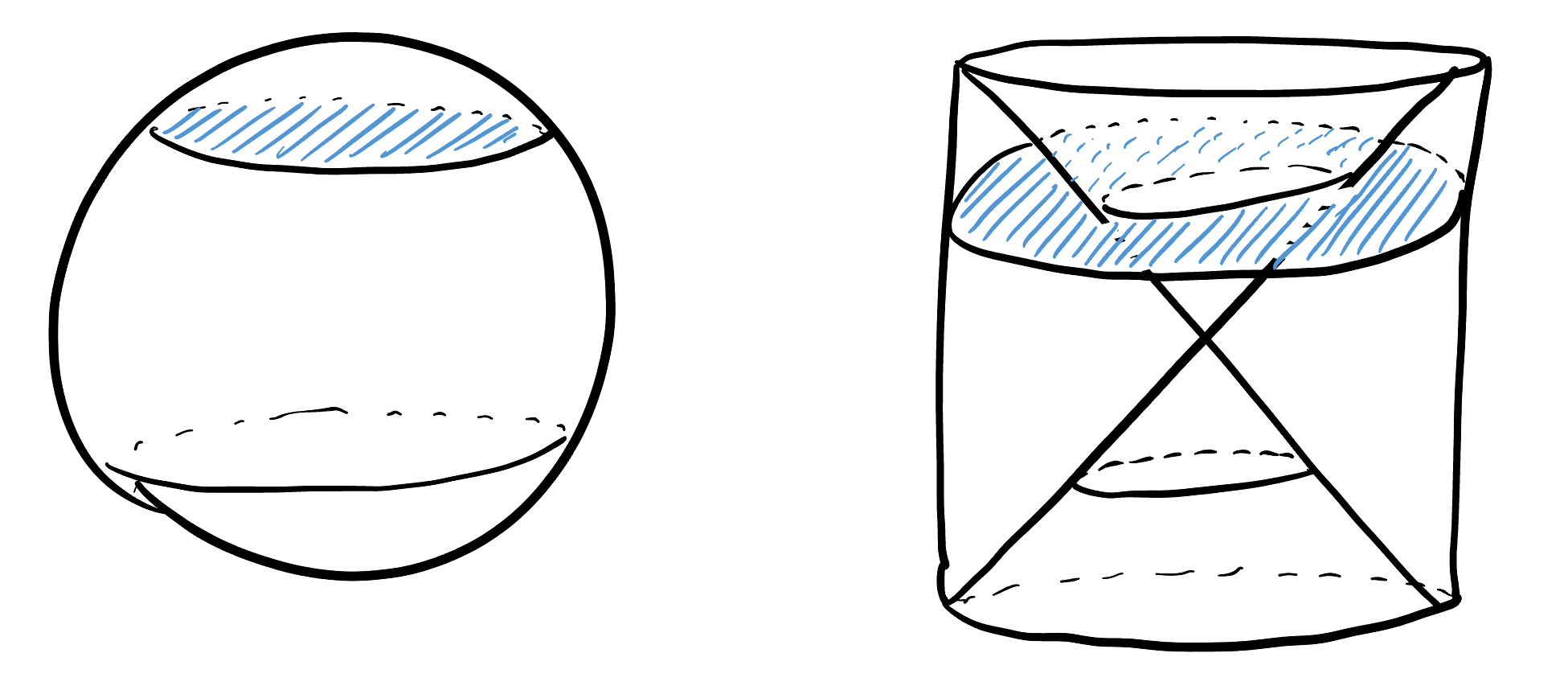
Archimedes original argument was by slicing: he imagined slicing each of these shapes by a plane at different heights, and he showed that at any given height \(z\), the cross sections of the two shapes had the same area.
'Exercise 16.4 Confirm Archimedes claim: show the slice of a sphere and cylinder-minus-cone at height \(z\) have the same areas, for any \(z\).
Then Archimedes noted that the volume of a region is the integral of the area of its slices (of course, not using these words, as they were not to be invented for another 1800 years!) and so two shapes with all the same cross sectional areas must have the same volumes.
He next computed the volume of a cylinder to be the area of its base times its height, and the area of a cone to be \(1/3\) its base times height. This gave him the formula
\[\mathrm{vol}(S_{p,r})=(\pi r^2)(2r)-\frac{1}{3}(\pi r^2)(2r)=\frac{2}{3}(\pi r^2)(2r)=\frac{4}{3}\pi r^3\]
But this immediately gives us the value of the sphere volume constant in terms of \(\pi\): thus all the constants for circles and spheres are just rational multiples of a single mysterious number!
Theorem 16.8 (Value of the Volume Constant) \[C_{Vol}= \frac{\mathrm{vol}(S_{p,r})}{r^3}=\frac{4}{3}\pi\]
Archimedes found this fact so striking and so beautiful that he asked for a Sphere and a Cylinder (the key ideas in this proof) to be engraved on his tombstone. As far as we can tell in the historical record, his wish was heeded when he died in 212BCE- but his grave was quickly forgotten to those living on his native island of Syracruse.
However, in 75BCE, the great Roman orator Cicero was visiting Syracruse and searched out Archimedes - then already known as the greatest mathematical mind in history, and found it due to this carving. In his own words:
“Once, while I was superintendent in Syracuse, I brought out from the dust Archimedes, a distinguished citizen of that city. In fact, I searched for his tomb, ignored by the Syracusans, surrounded on all sides and covered with brambles and weeds. The Syracusan denied absolutely that it existed, but I possessed the senari verses written on his tomb, according to which on top of the tomb of Archimedes a sphere with a cylinder had been placed. But I was examining everything with the eyes … And shortly after I noticed a small hill not far emerged from the bushes. On it there was the figure of a sphere and a cylinder. And I said immediately to the Syracusans “That’s what I wanted!” > Cicero, 75 BCE
16.2.3 Modern Computation
Having seen the beauty of the results which we are after, we will now seek to prove them with modern (calculus-based) methods. We find the volume of the sphere by slicing into disks, and we know the area of a disk from slicing it into line segments!

Because we know the number we are after is constant we are welcome to work directly with the unit sphere so that extra letters like radii don’t complicate our lives. Call this sphere \(S=S_{O,1}\). Then
\[\mathrm{vol}(S)=\iiint_S dV = \int_{-1}^1 \left(\iint_{C_r}dA\right)dz\]
Where \(C_r\) is the circle of radius \(r\) that we get by slicing horizontally at height \(z\). Because we know the area of a circle formula is \(\pi r^2\) we can subsitute this into our integral, and reduce it to a single integration!
\[\mathrm{vol}(S)=\int_{-1}^1 \pi r^2 \, dz\]
All that remains is to figure out the radius of the slice at height \(z\). This is easiest to do by looking at a side view where we can use the distance formula in a plane:
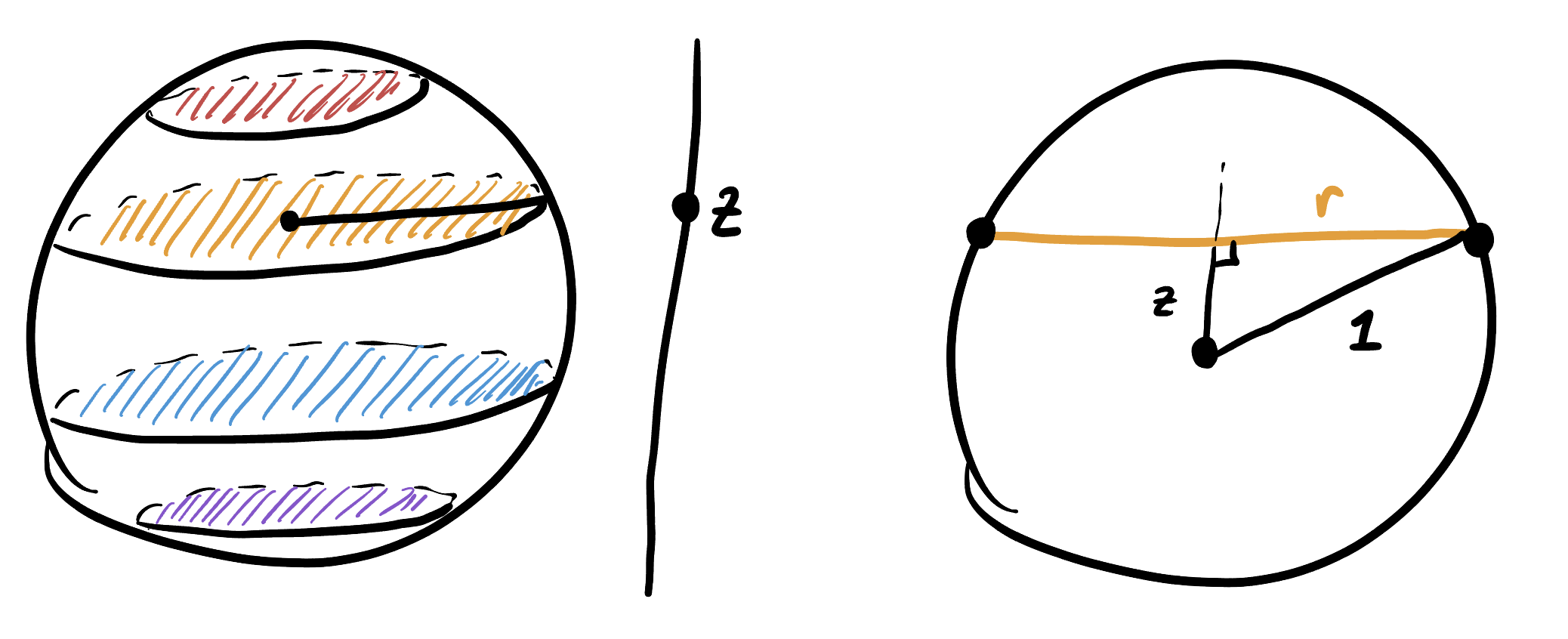
Alternatively we may just do this algebraically, and note that if \(x^2+y^2+z^2=1\) then \(x^2+y^2=1-z^2\), so at height \(z\) the points \((x,y)\) lie in a circle whose radius-squared is \(1-z^2\), or
\[r(z)=\sqrt{1-z^2}\]
Now plugging this into the area-of-a-disk formula, we can continue our integration by slicing:
\[\begin{align*}\mathrm{vol}(S)&=\int_{-1}^1 \pi \left(\sqrt{1-z^2}\right)^2\, dz\\ &=\pi \int_{-1}^1 1-z^2\, dz\\ &= \pi \left(z-\frac{z^3}{3}\right)\Bigg|_{-1}^1 \\&=\frac{4}{3}\pi \end{align*}\]
Because a homothety multiplies each infinitesimal length by its scaling factor, it increases the infinitesimal volume by the cube of the scaling factor. Thus, scaling up from the unit sphere to a sphere of radius \(r\) scales this as
\[\mathrm{vol}(S_{p,r})=\frac{4}{3}\pi r^3\]
Now, we can apply everything we learned thinking about circles to give a quick modern derivation of the area constant: area is the derivative of volume!
PICTURE
The reasoning goes through exactly analogously here: the difference quotient \(\mathrm{vol}(r+h)-\mathrm{vol}(r)\) is a thin spherical shell of thickness \(h\), so its volume is approximately the surface area of the shere times \(h\), and this approximation becomes exact as \(h\to 0\). Thus
\[\mathrm{area}(S_{p,r})=\frac{d}{dr}\mathrm{vol}(S_{p,r})=\frac{d}{dr}\frac{4}{3}\pi r^3=4\pi r^2\]
16.3 Higher Dimenisons
What about the fourth dimension? Can we fiigure out how spheres work there? The fact that lines are given by affine eqautions holds true in all dimensions, which allows us to write down the distance formula in \(4D\) and the equation of a sphere exactly as before.
To keep things simple we can start again with the 4-dimensional unit sphere, which is described by \[x^2+y^2+z^2+w^2=1\]
Let’s call this sphere \(H\) (or \(H_{O,1}\)) for hypersphere. We wish to find \(H\)’s volume by slicing, where we take three dimensional slices with constant \(w\): these slices will intersect the 4-dimensional ball by solid three dimensional balls much as we sliced the 3D ball into filled in 2d circles, and sliced circles into intervals!
It’s going to get difficult to keep dimensions straight here, so I’m going to start subscripting our volumes: I’ll write \(\mathrm{vol}_3\) for the usual three dimensional volume we know and love, and I’ll write \(\mathrm{vol}_4\) for the new four dimensional hypervolume. This slicing tells us
\[\begin{align*}\mathrm{vol}_4(H)&=\int_{-1}^1\left(\iiint_{S_r} dxdydz\right)dw\\ &=\int_{-1}^1 \mathrm{vol_3}(S_r) dw\\ &= \int_{-1}^1 \frac{4}{3}\pi r^3 \, dw \end{align*}\]
This leaves us once again with a single integral to do! And all we need is the relationship between the radius \(r\) and the height \(w\), which is exactly the same as in the dimension below:
\[r(w)=\sqrt{1-w^2}\]
In theory, all we have to do now is plug this in and integrate! In practice this integral is a bit more challenging than we have come across before (though nothing that you haven’t seen already in a Calculus II course)
\[\mathrm{vol}_4(H)=\frac{4\pi}{3}\int_{-1}^1 \left(\sqrt{1-w^2}\right)^3dw\]
This integral requires a trigonometric substitution to complete. It’s perhaps easier to deal with the bounds if we first realize the integral is an even function, and so we could instead just integrate on \([0,1]\) and double the result:
\[\frac{4}{3}\int_{-1}^1 \left(\sqrt{1-w^2}\right)^3dw=\frac{8\pi}{3}\int_0^1 \left(1-w^2\right)^{\frac{3}{2}}dw\]
Now we can make the substitution \(w=\sin\theta\), where we find \(w=0\) corresponds to \(\theta =0\) and \(w=1\) corresponds to \(\theta = \tau/4\) (as \(\sin\tau/4 = 1\)). After this substitution we have
\[\begin{align*} \mathrm{vol}_4(H)&=\frac{8\pi}{3}\int_0^{\tau/4}\left(1-\sin^2\theta\right)^{\frac{3}{2}}d\left(\sin\theta\right)\\ &= \frac{8\pi}{3}\int_0^\frac{\tau}{4}(\cos^2\theta)^{\frac{3}{2}}\cos\theta d\theta\\ &=\frac{8\pi}{3}\int_0^\frac{\tau}{4}\cos^4\theta d\theta \end{align*}\]
Now we have yet more work, as we have arrived at the integral of the fourth power of cosine. This requires some trigonometric work with the double/half angle identites we proved:
Exercise 16.5 (Integrating \(\cos^4(\theta)\)) Use the identity \(\cos^2 x = \frac{1}{2}(1+\cos 2\theta)\) twice to show that \[\cos^4(\theta)= \frac{3}{8}+\frac{\cos 2\theta}{4}+\frac{\cos 4\theta}{8}\]
Then use this to confirm that
\[\int_0^{\frac\tau 4}\cos^4\theta = \frac{3}{8}\frac{\tau}{4}\]
Putting this together with the above, we finally reach our answer (using that \(\tau=2\pi\))
\[\mathrm{vol}_4(H)=\frac{8\pi}{3}\frac{3}{8}\frac{\tau}{4}=\frac{\pi\tau}{4}=\frac{\pi^2}{2}\]
This is the first time that our constant has not been a rational multiple of \(\pi\), but instead a rational multiple of \(\pi^2\)! Since homotheties scale four dimensional volumes by a factor of \(r^4\), we get that the full volume formula for a hypersphere of radius \(r\)
Theorem 16.9 (Volume of the Hypersphere) The volume of the 4-dimensional hypersphere of radius \(r\) is \[\mathrm{vol}_4(H_{p,r})=\frac{\pi^2}{2}r^4\]
From this we can get the three dimensional surface area by differentiation. Again to keep things straight, I’ll write \(\mathrm{area}_3\) for the three dimensional analog of surface area in 4D space, and \(\mathrm{area}_2\) for the usual 2D area in 3D space that we have thus far been just calling \(\mathrm{area}\).
Theorem 16.10 (Surface of the Hypersphere) \[\mathrm{area}_3(H_{p,r})=\frac{d}{dr}\mathrm{vol_4}(H_p,r)=\frac{d}{dr}\frac{\pi^2}{2}r^4=2\pi^2r^3\]
Thus, the 3-dimensional surface area constant for hyperspheres is \(2\pi^2\): also a multiple of \(\pi^2\) because it arose from differentiating volume.
Exercise 16.6 Find the volume and surface area constants for the 5-dimensional sphere via integration by slicing (for volume) and then differentiation (for surface area).
16.4 A Surprise in Even Dimensions
If you complete Exercise 16.6 above, you’ll find that the 5-volume has a rather strange-looking constant out front:
\[\mathrm{vol}_5=\frac{8}{15}\pi^2 r^5\]
What can we do with this information? Carry on the march to higher dimensions of course! If we try to find the volume of the unit 6-sphere by slicing, (say the axis we slice along is called \(w\) again, for convenience) we can write
\[\begin{align*}\mathrm{vol}_6 &= \int_{-1}^1 \mathrm{vol}_5(\sqrt{1-w^2})dw\\ &=\int_{-1}^1 \frac{8}{15}\pi^2 \left(\sqrt{1-w^2}\right)^5\,dw\\ &=2\frac{8}{15}\pi^2\int_0^1 \left(\sqrt{1-w^2}\right)^5\,dw \end{align*}\]
Unfortunately this time (again!) we cannot get rid of the square root since \(5\) is an odd power, and we must resort to a trigonometric substitution \(w=\sin\theta\). Skipping the now-familiar steps,
\[\int_0^1 \left(\sqrt{1-w^2}\right)^5\,dw =\int_0^{\frac\tau 4}\cos^6\theta\,d\theta\]
Now we need only expand out \(\cos^6\) via trigonometric identities and integrate:
Exercise 16.7 Confirm, similarly to a previous exericse that
\[\int \cos^6\theta\,d\theta =\frac{5}{16}x+\frac{15}{64}\sin(2\theta)+\frac{3}{64}\sin(4\theta)+\frac{1}{192}\sin(6\theta) \]
And thus, that the definite integral we are after is
\[\int_0^{\frac\tau 4}\cos^6\theta\,d\theta = \frac{5}{16}\frac{\tau}{4}\]
Plugging this back into our original expression we get some almost magical cancellation of all these constants:
\[\begin{align*}\mathrm{vol}_6&=2\frac{8}{15}\pi^2\frac{5}{16}\frac{\tau}{4}\\ &=\frac{\pi^2}{3}\frac{\tau}{4}\\ &=\frac{\pi^2}{3}\frac{\pi}{2}\\ &=\frac{\pi^3}{6} \end{align*}\]
Theorem 16.11 (Volume of the 6-Sphere) The volume of the six dimensional sphere of radius \(r\) is
\[\frac{\pi^3}{6}r^6\]
From here - if we were feeling brave - we could calculate the volume of the seven-dimensional ball by slicing (which would not need a trig sub, as the slices are 6 dimensional and the sixth power will get rid of the square root) yeilding
\[\mathrm{vol}_7=\frac{16}{105}\pi^3\]
Then use this to calculate the volume of the 8-dimensional ball by slicing (which will now need another trig sub, which will introduce another factor of \(\pi\) through the bound \(\tau/4\)). The result here has some ugly calculation and marvelous cancellations, ending with
\[\mathrm{vol}_8 = \frac{\pi^4}{24}\]
A pretty interesting pattern is arising here - using \(\mathrm{vol}_2\) for the two dimensional volume (area) of a circle, we have
\[\mathrm{vol}_2 = \pi\hspace{1cm}\mathrm{vol}_4=\frac{\pi^2}{2}\hspace{1cm}\mathrm{vol}_6=\frac{\pi^3}{6}\hspace{1cm}\mathrm{vol}_8=\frac{\pi^4}{24}\]
It appears that the volume of the \(2n\) dimensional ball is \(\pi^n/n!\). Incredibly, this turns out to be correct:
Theorem 16.12 (Even volumes) \[\mathrm{vol}_{2n}=\frac{\pi^n}{n!}\]
One way to prove this is to continue the process we have been doing, with the trig subs and all, but via induction (and being clever, realizing we only need to know the constant term of \(\cos^{2n}(\theta)\) - all the rest integrate to zero every time!)
But there’s an alternative way - one can try to integrate via slicing over two dimensions at once, and get a recurrence relation relating the volume in dimension \(n\) to the volume in dimension \(n-2\):
Proposition 16.1 \[\mathrm{vol}_n=\frac{\pi}{n}\mathrm{vol}_{n-2}\]
If you’re interested in doing this - come talk to me in office hours! But now for the truly strange part: what is the sum of the volumes of all the even dimensional balls?
\[\sum_{n\geq 0 }\mathrm{vol}_{2n}=\sum_{n\geq 0}\frac{\pi^n}{n!}=e^\pi\]
WHAT?! This is the series expasion of \(e^x\) evaluated at \(\pi\). But it gets even crazier. What if we add up the volumes of the spheres of radius \(r\)? This multiplies each term by \(r^{2n}\) (since they are even dimensional spheres) and equals
\[\sum_{n\geq 0}\frac{\pi^n}{n!}r^{2n}=\sum_{n\geq 0}\frac{(\pi r^2)^n}{n!}=e^{\pi r^2}\]
Why in the world is the sum of the volume of all the even dimensional balls what you get by plugging the area of the circle into the exponential function?! I have no idea…