2 Parallels
The fifth postulate of Euclid is often called the parallel postulate, as it gives a condition that can be checked for whether or not two lines are parallel.
Definition 2.1 (Parallel) Two lines are parallel if they do not intersect.
Why the parallel postulate was suspicious to take as an axiom to the ancients.
One reason often cited: its complexity! Its a long statement.
But better reason, it implies the EXISTENCE of something (an intersection) at an arbitrary distance. The other postulates only assure the existence of things on scales that arleady show up in problem (given a segment, it can be extended finitely. Given a length, you can make a circle with it.)
2.0.1 Equivalents to Postulate 5
Definition 2.2 (Equivalence to Parallel Postulate) A postulate
One cleaner statement equivalent to Postulate 5 was already known to Proclus in antiquity, but became widely recognized after John Playfair’s 1795 commentary on the Elements:
Definition 2.3 (Playfair’s Axiom) In a plane, given a line and a point not on it, a unique line parallel to the given line can be drawn through the point.
Remark 2.1. Often Playfair’s axiom is stated more generally, and only asserts that at most one line parallel to a given line can be drawn. However, it is possible to prove directly from Euclids Postulates 1-4 that parallel lines exist (Book I Proposition 31): so our formulation is equivalent.
This does away with much of the seeming complexity of the original postulate, replacing the condition of precise angle measures and intersections with the stipulation that parallel lines are unique. However this does not help with the more substantive point of unease, that Postulate 5 says something about what is going on arbitrarily far away. After all, how do you check that a parallel line is unique other than to check that all other lines make some intersection, even though many of those intersections will be unobservably far away.
In 1733, a Jesuit Priest and geometer by the name of Giovanni Saccheri made a useful, and prescient observation. He asked himself, what are all the logical possible statements that could take the place of Euclid’s 5th postulate, or the (now-called) Playfair’s Axiom? Well, if the axiom states that there exists a unique parallel through a given point, the other logical choices are that there are none or there are many.

Saccheri attempted to draw a contradiction from the other cases with Euclid’s other four postulates, and while his investigations did not quite succeed, they led in some very interesting directions we will return to later on.
In the millennium and a half span from Proclus until the 1800s, many other foundational theorems of Euclidean geometry were also shown to be equivalent to the 5th. Among these are the following short list:
Theorem 2.1 (Some Equivalents to the Parallel Postulate) The following postulates are equivalent to the parallel postulate:
- All triangles have angle sum
- At least one rectangle exists.
- There exist triangles of arbitrarily large area
- Circumference/Radius is a constant for circles
- Area/Radius Squared is a constant for circles
- Equidistant curves to a line are lines
- There exists a pair of triangles which are similar, but not congruent
- The pythagorean theorem is true
- Given any 3 non-collinear points, there is a circle passing through them.
- Any two parallel lines have a common perpendicular.
All of these properties are true of the world around us, and some of them (like the statement that rectangles exist) are even finitely checkable: it seems inconceivable to imagine a world where they were false! Yet, for over two millennia mathematicians the world over tried - and failed - to prove any single one of these statements from the first four postulates of Euclid alone.
The reason for this is grander than any of them could imagine, until Gauss, Lobachevsky and Bolyai entered the scene in the early 1800s. No one could prove any of these statements from the first four because they are not implied by the first four! There are logically possible, consistent mathematical worlds which act very similar to the geometry we find around us on earth, but for which the Pythagorean theorem is false. We will encounter these worlds (hyperbolic geometries) in the second half of this course.
2.1 Proofs: Triangles
To recover all of geometry in its full glory, he first invokes the 5th postulate in Proposition 29, which is restated below.
Proposition 2.1 (Alternate Angles are Equal (Euclid Prop 29)) A straight line falling on parallel straight lines makes the alternate angles equal to one another
Before we can prove this however, we need to talk a little bit about how the greeks measured angles. Euclid has several criteria called common notions he uses to axiomatize the means of measuring quantities such as angle, length, and area. For us in this short introduction, we will summarize some of these in the following “angle axioms”.
Definition 2.4 (Angle Axioms)
- Any two congruent angles have the same measure.
- If an angle
To get accustomed to these, we will first prove a practice result comparing angles, which does not need the parallel postulate.
Proposition 2.2 (Opposite Angles are Equal) If two lines intersect at a point in
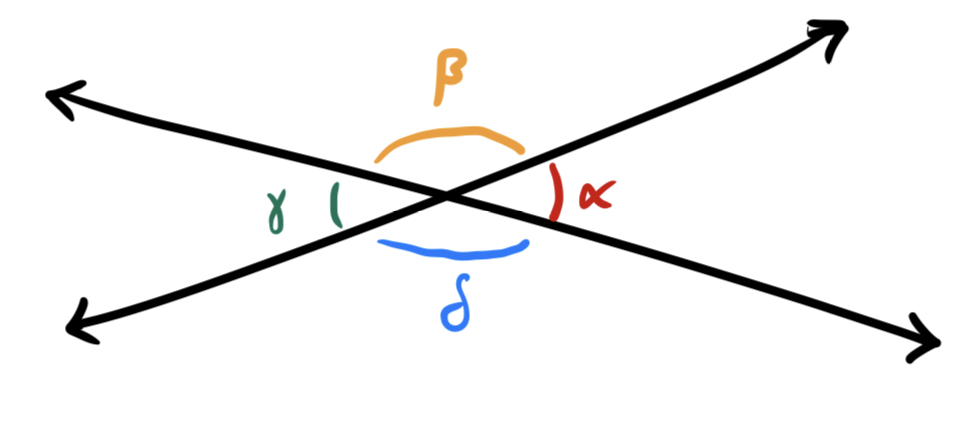
Remark 2.2. Here we have used that any two angles which sum to a straight line equal two right angles, as two right angles also form a straight line. Euclid proves this separately as Proposition 13.
Proof. Let two lines cross at a point, determining the four angles labled
Next, we’ll prove our first lemma that does invoke the parallel postulate:
Proposition 2.3 (Corresponding Angles are Equal) If a line crosses a pair of parallel lines, the angles it makes with each of the parallel lines are equal in measure.

Proof. Let
Because
Subtracting
Now we have enough information assembled to complete the task at hand.
Proving Euclid 29

Proof. Again let
We have barely begun our use of the parallel postulate (we so far have used it precisely once, in a lemma about corresponding angles), but even just letting touch our theory is enough to have profound consequenes.
Theorem 2.2 (Triangles have Angle-Sum
Below I give a proof using not the Parallel Postulate directly, but using the equivalent Playfair’s axiom, that parallel lines exist and are unique. Check Euclid Proposition 32 for the original proof.
Proof. Consider an arbitrary triangle

By Playfair’s Axiom (Definition 2.3), there is a unique line through

Note that the opposite interior angles formed by two sides of the triangle with the pair of parallel lines are equal (Proposition 2.1).

Thus, the straight line at the top is the sum of all three angles of the triangle! In radians, this sum is
Exercise 2.1 (Polygon Angle Sum) A polygon is convex if all of its angles are less than
Prove that the angle sum of convex quadrilaterals is a constant, for all quadrilaterals. Prove the angle sum of convex pentagons is also a constant. What are these constants?
What do you think the formula is for the sum of angles in a convex

2.2 Quadrilaterals
Definition 2.5 (Quadrilaterals) A quadrilateral is a polygon with four straight line sides. If all four angles are right angles, it is called a rectangle. A rectangle with all sides the same length is a square. If opposing sides are segments of parallel lines, its called a parallelogram.
Finally, we’ve uncovered enough to move beyond triangles a bit!
Theorem 2.3 (Rectangles Exist) There exists a quadrilateral in the plane, all of whose angles are right angles.
Exercise 2.2 Prove Theorem 2.3 using Euclid’s Postulates (and also Playfair’s Axiom, if you like it), and the propositions given so far in this section.
Hint - we know how to make right angles now, and parallel lines through points. Start making some!
In fact (you may or may not have concluded this in your proof, depending on how general you were), for any lengths
Proposition 2.4 (Rectangles have Congruent Opposite Sides) Let
Proof.
- Start with an arbitrary rectangle, and extend its sides into lines.
- Looking at one of the sides, it crosses the other pair in two right angles (by definition: its a rectangle). Thus the angle sum is a straight line, and so this other pair of sides is parallel, by the 5th postulate.
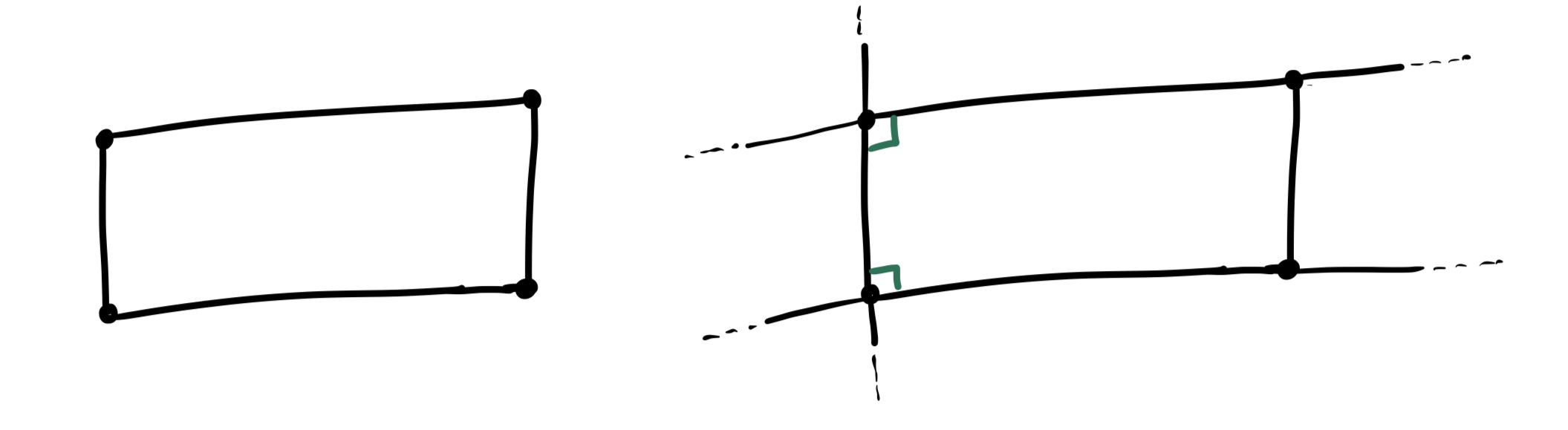
- Draw a diagonal connecting an opposing pair of vertices of the rectangle.
- This diagonal divides the rectangle into two triangles, which both share a common side.
- But, since the this diagonal cuts across a pair of parallel lines, its alternate angles are equal.

- Thus, the two triangles that have been formed are congruent to one another, by Angle-Side-Angle.
- But if the triangles are congruent, then they have the same side lengths.
- Thus, each pair of opposing sides of the rectangle must have the same length.

Running the same argument with the other diagonal also gives a pair of triangles congruent to these, thus the diagonals of a rectangle must be equal in length to one another. In fact, more is true: the point where the diagonals intersect one another divides each of the diagonals in half - the Greeks would say their intersection bisects both of the diagonals.
A good way to get a feel for Euclidean geometry is to try and play around with properties like this that you discover. So, rectangles diagonals bisect one another, but is this all? Playing around a bit, its easy to see there should be more examples (draw any two line segments that cut each other in half making some sort of
Exercise 2.3 (Bisecting Diagonals = Parallel Sides) If the diagonals of a convex quadrilateral bisect one another, then that quadrilateral is a parallelogram.