$$ \newcommand{\RR}{\mathbb{R}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\CC}{\mathbb{C}} \newcommand{\NN}{\mathbb{N}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\EE}{\mathbb{E}} \newcommand{\HH}{\mathbb{H}} \renewcommand{\SS}{\mathbb{S}} \newcommand{\DD}{\mathbb{D}} \newcommand{\pp}{^{\prime\prime}} \newcommand{\p}{^\prime} \newcommand{\proj}{\operatorname{proj}} \newcommand{\area}{\operatorname{area}} \newcommand{\len}{\operatorname{length}} \newcommand{\acc}{\operatorname{acc}} \newcommand{\ang}{\sphericalangle} \newcommand{\map}{\mathrm{map}} \newcommand{\SO}{\operatorname{SO}} \newcommand{\dist}{\operatorname{dist}} \newcommand{\length}{\operatorname{length}} \newcommand{\uppersum}[1]{{\textstyle\sum^+_{#1}}} \newcommand{\lowersum}[1]{{\textstyle\sum^-_{#1}}} \newcommand{\upperint}[1]{{\textstyle\smallint^+_{#1}}} \newcommand{\lowerint}[1]{{\textstyle\smallint^-_{#1}}} \newcommand{\rsum}[1]{{\textstyle\sum_{#1}}} \newcommand{\partitions}[1]{\mathcal{P}_{#1}} \newcommand{\erf}{\operatorname{erf}} \newcommand{\pmat}[1]{\begin{pmatrix}#1\end{pmatrix}} \newcommand{\smat}[1]{\left(\begin{smallmatrix}#1\end{smallmatrix}\right)} $$

13 Shapes

Defining the notion of lines and distance really helps in getting our new geometry off the ground. In this relatively short chapter, we give precise definitions for familar shapes: including polygons and cirlces, but also other conic sections - parabolas, ellipses, and hyperbolas known to the ancient Greeks.

13.1 Polygons

Definition 13.1 (Polygon) A polygonal chain is a sequence $L_1,L_2,\ldots, L_n$ of line segments, where the ending vertex of $L_n$ coincides with the starting vertex of $L_{n+1}$.

A polygon is a closed, non-intersecting polygonal chain. The interior of a polygon is called a polygonal region.

A polygonal chain (left) and a polygon (right). The polygonal region is shaded red.

A triangle is a polygon with three sides, a quadrilateral is a polygon with four sides, and so on. We will study polygons in more detail later on, especially in the curved geometries of the sphere and hyperbolic space. But for now, we content ourselves in getting used to the definitions by re-proving some familiar results of the greeks.

Exercise 13.1 (Constructing an Equilateral Triangle) Beginning with the segment $[0,\ell]$ along the $x$-axis, construct an equilateral triangle by finding the coordinates of a point $p=(x,y)\in\EE^2$ which is equidistant from both endpoints of the segment.

Exercise 13.2 (Equilaterals of Half the Size, Reprise) Re-prove that inside of an equilateral triangle, you can inscribe a smaller one with exactly half the side length. You already did this problem, using Euclid’s Axioms, but now we can do it much easier in our new foundations!
Hint: just find where the vertices should be, and then measure the distances between them!

13.2 Circles

Euclid’s definition of a circle is as follows: A circle is a plane figure bounded by one curved line, and such that all straight lines drawn from a certain point within it to the bounding line, are equal. In modern terminology, we may phrase this as below:

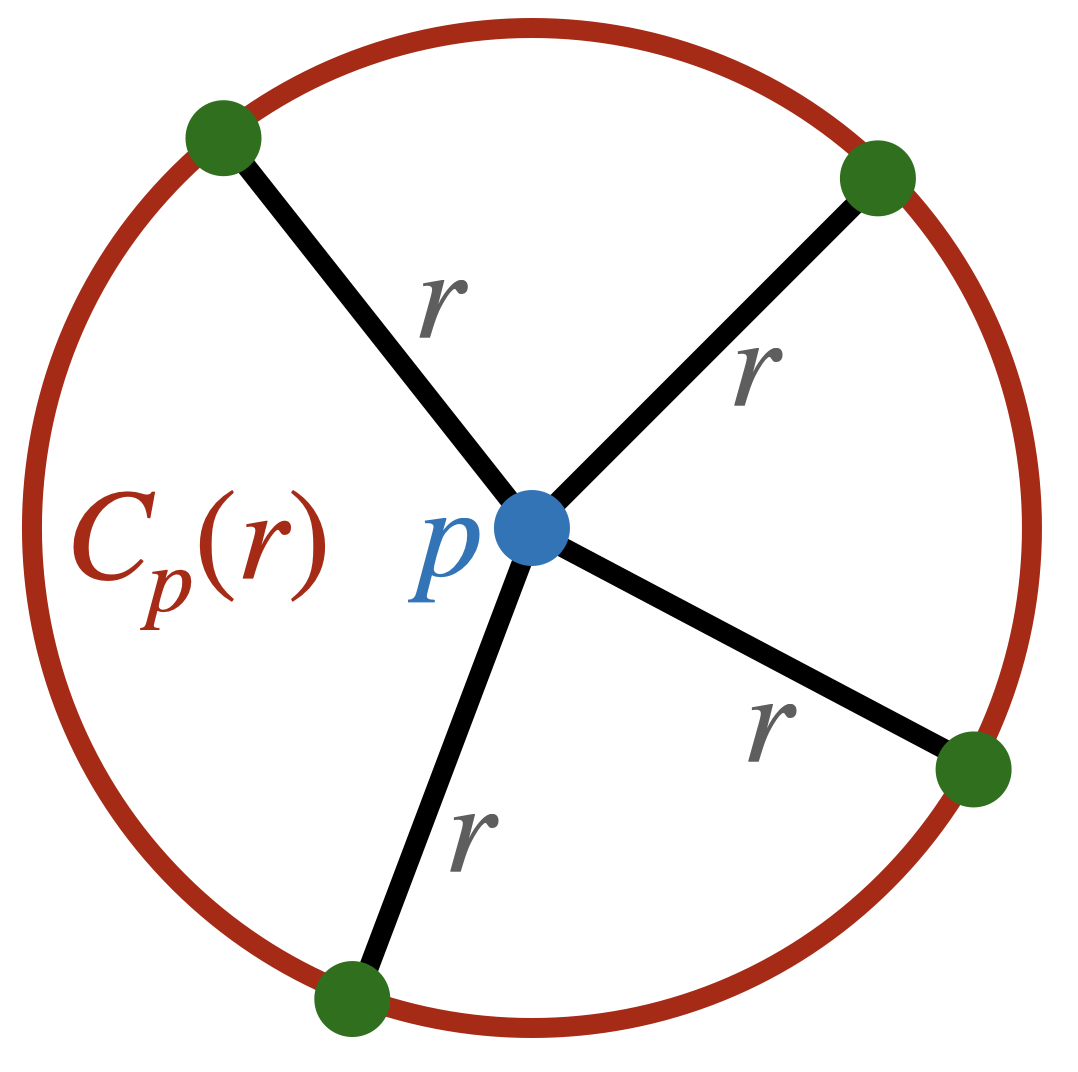
The circle $C_p(r)$ is the set of points at distance $r$ from a fixed point $p$.

Definition 13.2 A circle centered at a point $c\in\EE^2$ is a curve such that the distance between $p$ and any point on the curve is the same. This fixed distance is called the radius of the circle. We denote the circle of radius $r$ centered at $p$ as $C_p(r)$.

Now that we know the distance function on $\EE^2$ we can formally write down the equation of a circle directly from this definition.

Theorem 13.1 The circle of radius $r$ centered at $p=(h,k)$ is given by the set \[C_p(r)=\left\{q=(x,y)\in\EE^2 \mid (x-h)^2+(y-k)^2=r^2\right\}\]

Proof. This is just a direct computation: if $q=(x,y)$ is an arbitrary point in the plane, its distance from $p=(h,k)$ is \[\dist(q,p)=\|q-p\|=\sqrt{(x-h)^2+(y-k)^2}\] For $q$ to lie on the circle, this distance needs to be set equal to $r$. The equation is easier to work with after squaring both sides to remove the square root, giving \[(x-h)^2+(y-k)^2=r^2\]

Corollary 13.1 (Proving Euclid’s Axiom III) Given any point $p$, and any radius $r$, the circle $C_p(r)$ exists.

Proof. Now that we have the actual equation for a circle, Euclid’s axiom is rather straightforwardly true. Saying we can draw a circle about any point of any radius is just asserting that the equation \[(x-h)^2+(y-k)^2=r^2\] has solutions for every $h,k,r$. And this in turn is just a property of the real numbers, and the existence of square roots! For simplicity considering the case centered at $0$, for any $x\in [-r,r]$ we can solve directly for $y=\pm\sqrt{r^2-x^2}$, which is a real number as $r>|x|$ so $r^2-x^2$ is positive, and all positive reals have real square roots!

One intuitive result about circles that we will use a lot in the near future is that any isometry of the plane that fixes the circles center must preserve the circle:

Proposition 13.1 (Isometries Fixing the Center Preserve the Circle) Let $C_c(r)$ be a circle centered at $c$, and $\phi$ be any isometry of $\EE^2$ sending $c$ to itself. Then $\phi$ preserves $C$: that is, if $p$ is any point on $C$, $\phi(p)$ is also on $C$.

Proof. Let $C_c(r)$ bea circle, and $\phi$ an isometry fixing $c$. If $p\in C_c(r)$ is any point, then by definition $\dist(p,c)=r$. Applying the isometry $\phi$, since isometries do not affect distances, we see \[r=\dist(p,c)=\dist(\phi(p),\phi(c))=\dist(\phi(p),c)\] Where the second inequality is because $\phi(c)=c$. But this says the distance from $\phi(p)$ to the circles center is also $r$, so $\phi(p)$ lies on the circle! Thus $\phi$ sends the circle to itself.

If an isometry fixes the center of a circle, it sends the entire circle to itself.

Exercise 13.3 Prove that applying any isometry or similarity to a circle results in another circle.

Computations

Recall that in all of Euclid’s axioms, conditions for intersections with circles were never specified! Indeed - Euclid intersected two circles in his construction of the equilateral triangle. Now that we have a precise description of circles in our new foundations, we can fix this gap:

Exercise 13.4 Prove that two circles intersect each other if the distance between their centers is less than or equal to the sum of their radii.

Hint: start by applying an isometry to move one of the circles to have center $(0,0)$, and then another isometry to roate everything so the second circle has center $(x,0)$ along the $x$-axis. This will make computations easier!

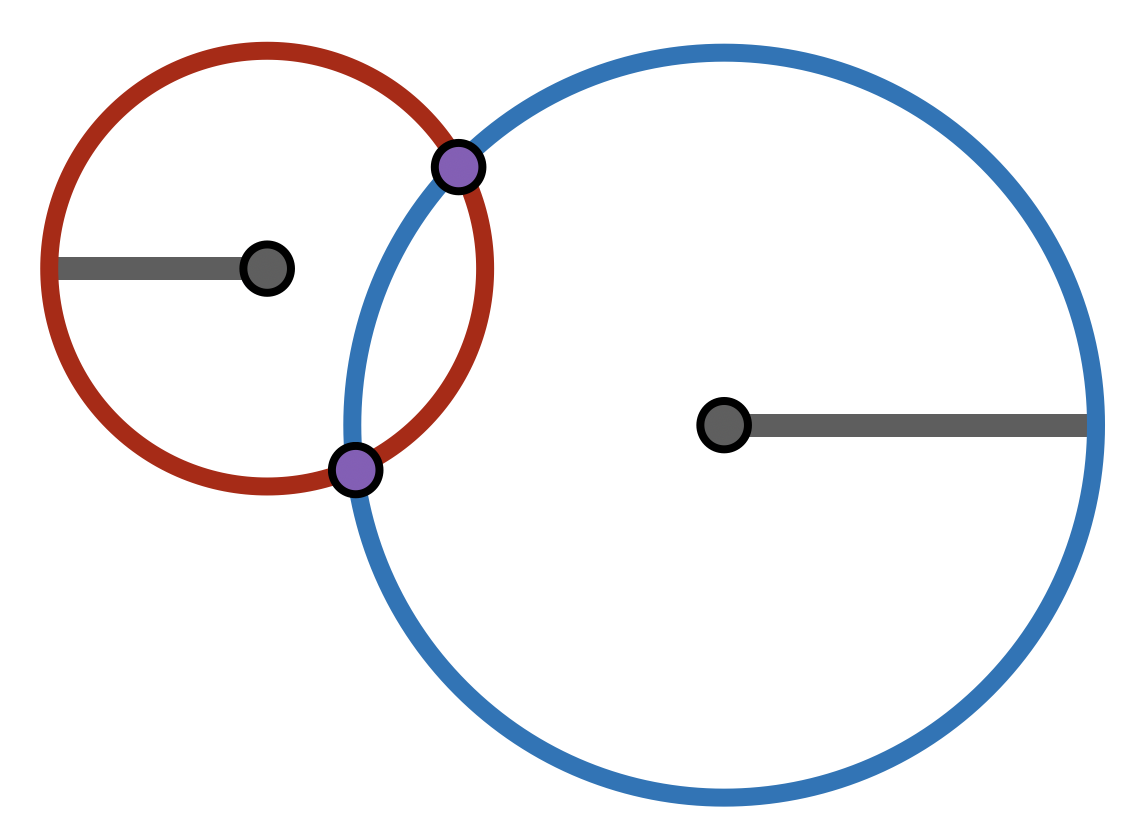
Two circles intersect if the distance between their centers is less than or equal to the sum of their radii.

The other case that is interesting but does not appear in Euclid is the intersection of a circle an a line.

Exercise 13.5 (Circles Intersecting Lines) Prove that a circle intersects a line whenever the shortest distance from that line to the circles center is less than the circles’ radius.

Hint: start by applying an isometry that either (1) moves the line to the $x$ axis, or (2): moves the circle’s center to the origin - whichever one makes the computation easier for you!

13.3 Application: Classifying Isometries

The above exercises allowed us to compute exactly when two circles intersect - and crucially: how many times they do so. While our motivating reason to compute these things may have been to fill a gap in Euclid, this information can take us quite far when used correctly. Indeed, here we show that it is the key which allows us to classify all possible isometries of the plane!

We have discovered many isometries so far - translations, rotations (both about $O$ and other points), reflections across lines, and all possible combinations thereof by composition and inversions. However, we have conducted no methodological search for isometries and so there is no good reason to think we are done. In fact, it seems dauntingly hard to ever prove we have found them all: who is to say that theres not some absurdly complicated function we have never thought of, that still preserves all infinitesimal lengths?

One way to begin making progress on this question is to ask how much information do you need to completely determine an isometry? Is it possible that there could be two isometries that act like exactly the same function inside some region, but differ elsewhere? If so, that would mean it will be very hard to track down all isometries! But if not, we could ask ourselves what is the smallest region we need to understand an isometry on to specify it uniquely. And the answer is rather suprisingly minimal!

Proposition 13.2 (Isometries Fixing 3 Points) Let $p,q,r$ be a triple of non-collinear points in the plane. If an isometry $\phi$ fixes all three points, then $\phi$ is the identity.

Proof. Let $p,q,r$ be three noncollinear points, and $\phi$ an isometry with $\phi(p)=p$, $\phi(q)=q$ and $\phi(r)=r$. We aim to show that $\phi$ is the identity: so we will consider an arbitrary point $a$ in the plane, and show that $\phi(a)=a$. To do so, it will prove important to pay attention to the distance between $a$ and the points $p,q,r$.

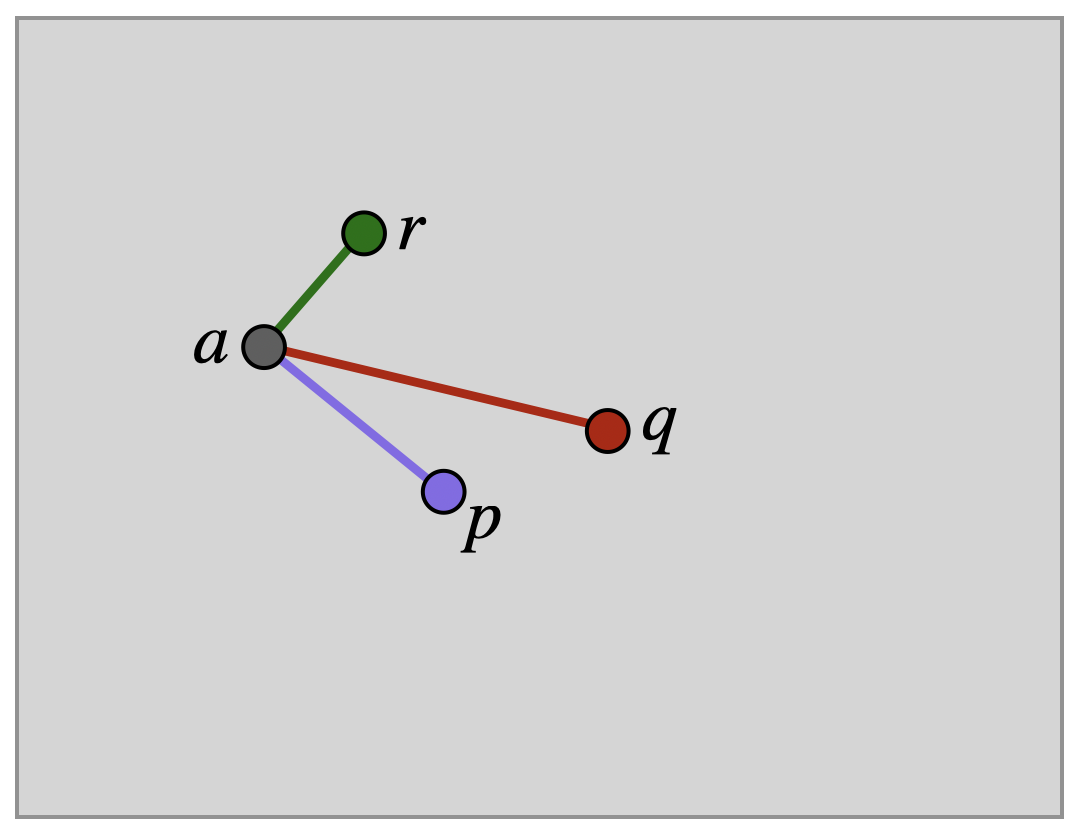
The fixed points $p,q,r$ and their distances to an arbitrary point $a$.

First, look at $p$. Since $\phi$ is an isometry we know $\dist(a,p)=\dist(\phi(a),\phi(p))$: but $\phi$ fixes $p$! Thus $a$ and $\phi(a)$ are at the same distance from $p$, and lie on a circle centered at $p$.

Both $a and $\phi(a)$ must lie on the same circle centered at $p$.

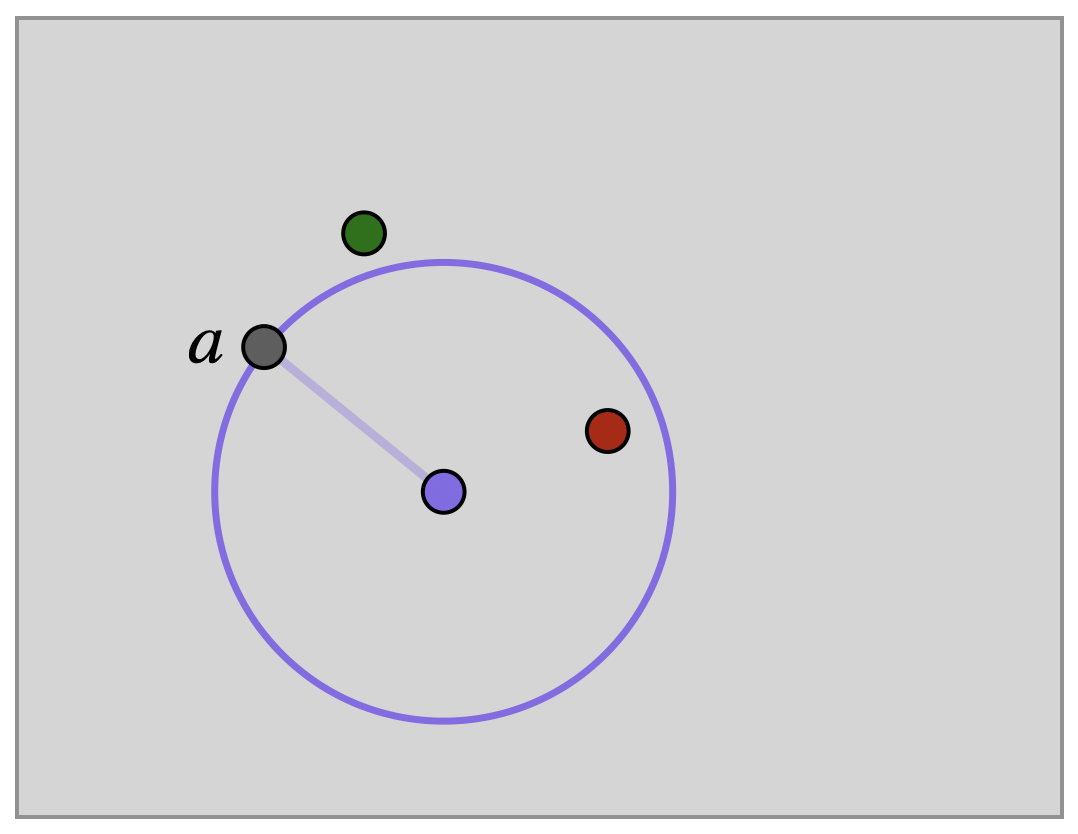
As $q$ is also fixed by $\phi$, we similarly see that both $a$ and $\phi(a)$ must lie on the same circle centered at $q$.

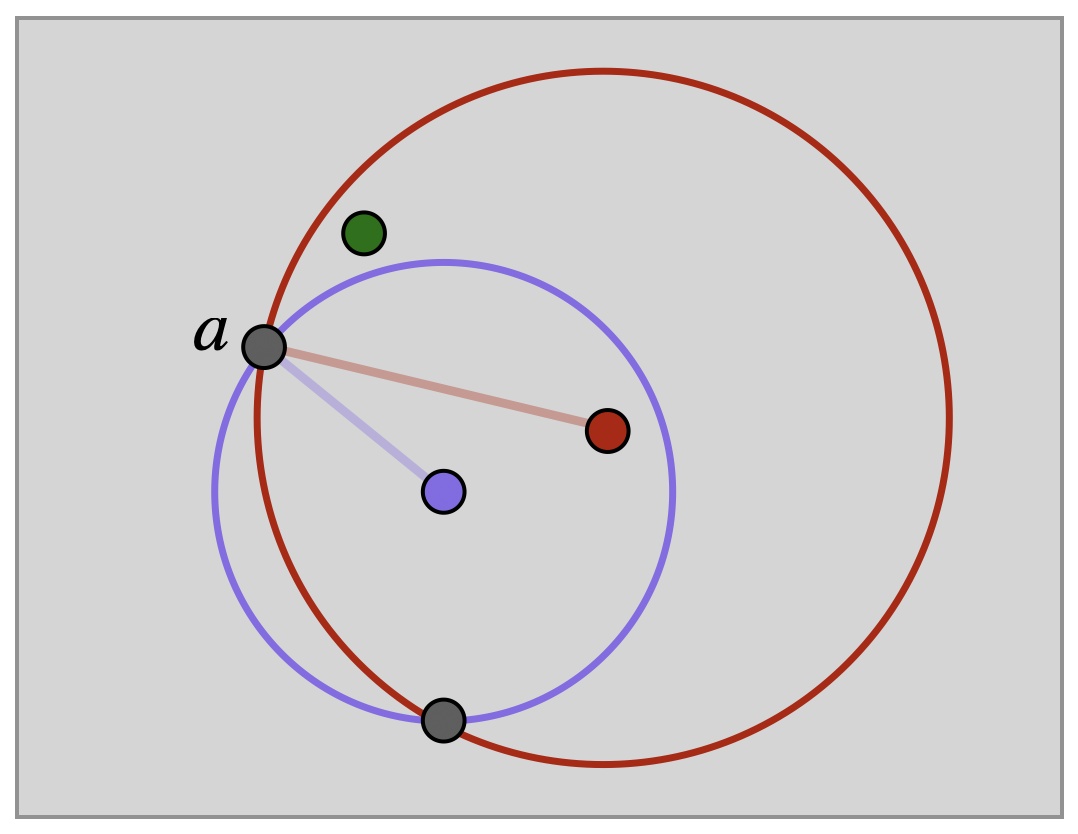
BThe same is true for $q$. So both $a$ and $\phi(a)$ must lie on both of these circles!.

However by Exercise 5, we know that generically circles will intersect in two points, so from the information we have so far, its not guaranteed that $a$ and $\phi(a)$ are the same point: one could be at each intersection. But this isn’t surprising as we haven’t considered all the information at hand! We also know that $\phi$ fixed $r$ and so both $a$ and $\phi(a)$ must lie on the same circle centered at $r$.

Because $p,q$ and $r$ are noncollinear, these three circles cann only intersect at a single point! This point must be both $a$ and $\phi(a)$, so $\phi$ fixes $a$.

Each pair of these circles intersects in two points. And, as the points are noncollinear, all three circles intersect in a single point (homework exercise, below). But this must be both $a$ and $\phi(a)$: thus $\phi(a)=a$!

And $a$ was an arbirary point, and we showed that $\phi$ did not move it. This means $\phi$ must not move any points at all in the plane - so $\phi$ is the identity!

Remark 13.1. In special cases (when $a$ lies at the midpoint of the line segment determined by $p$ and $q$) the circles centered at $p$ and $q$ through $a$ are tangent at $a$, making this their only point of intersection. In this case, we already know $a=\phi(a)$ even without considering $r$.

Exercise 13.6 (Circle Triple Intersection) Three circles with non-collinear centers can intersect in at most one point.

Hint: use some isometries to simmplify the situation: move everything so that two of the circles center’s are on the $x$ axis, and the third is on the $y$ axis.

PICTUREs

Corollary 13.2 (Isometries Agreeing on 3 Points are Equal) If $\phi$ and $\psi$ are two isometries of the plane which agree on a set of three non-collinear points, then they are equal.

Proof. Let $p_1,p_2,p_3$ be three points for which $\phi(p_i)=\psi(q_i)$. Now consider the isometry $\psi^{-1}\circ\phi$. This isometry actually fixes each of the three $p_i$ (since $\phi$ sends them somewhere, and $\psi^{-1}$ brings them back). Thus, by Proposition 13.2 this is the identity. But if $\psi^{-1}\phi=\mathrm{id}$ then composing with $\psi$ shows \[\phi=\psi\]

Using this, we can prove that we have actually found all the isometries, by starting from an arbitrary isometry and building it using only translations, rotations, and reflections.

Theorem 13.2 (Classification of Isometries) Every isometry of $\EE^2$ is a composition of reflection, rotation, and translation.

Proof. Let $\phi$ be an arbitrary isometry of the plane. and consider the three points $O$, $p=(1,0)$ and $q=(\tfrac{1}{2},\tfrac{\sqrt{3}}{2})$ forming the vertices of an equilateral triangle.

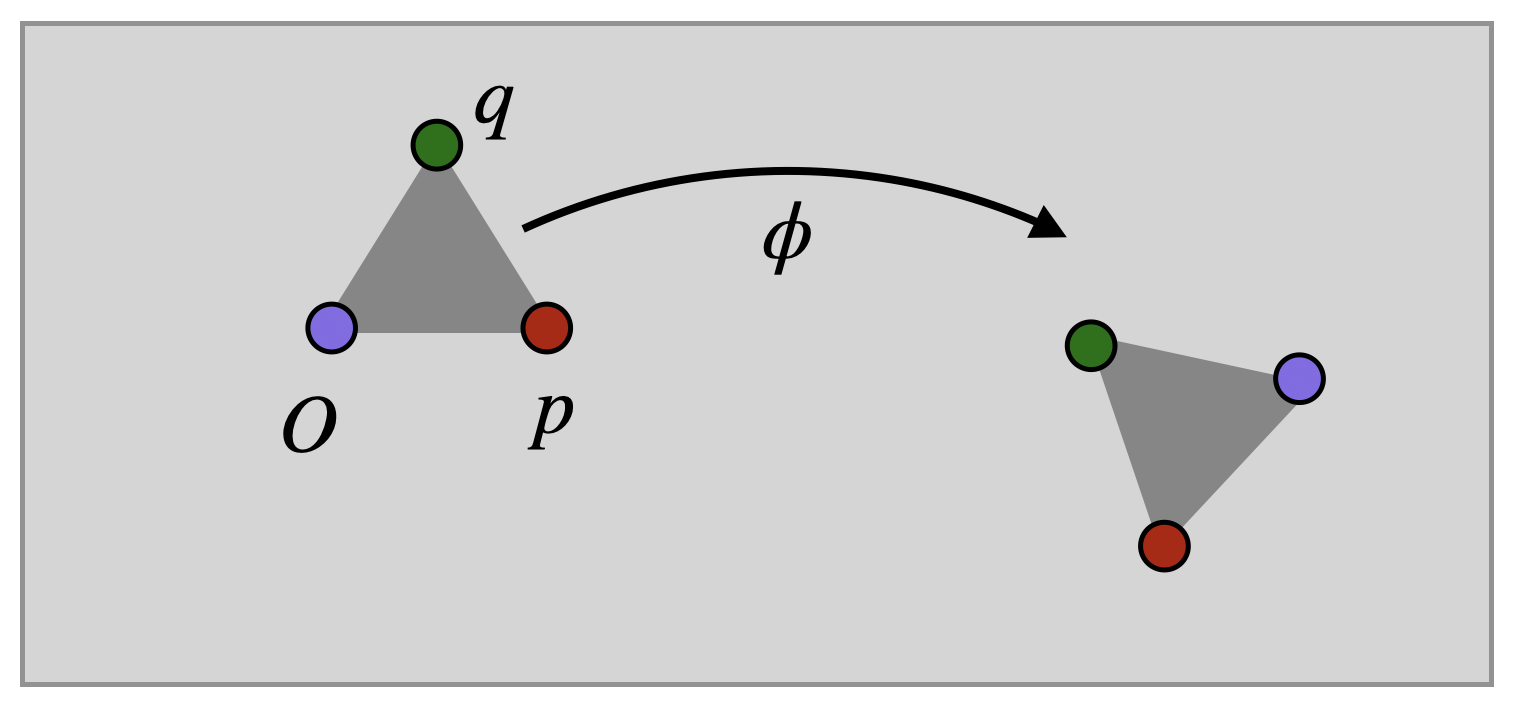
An isometry taking pne triple of points to another.

The isometry $\phi$ sends $O$ somewhere: let $T$ be a translation of the plane taking $\phi(O)$ to $O$. Now, the composition $T\phi$ fixes the origin! The point $p$ lies at distance $1$ from $O$, so the $T\phi$ takes it to another point unit distance away - call this point $r$.

Let $R$ be a rotation isometry fixing $O$ but taking $r$ back to $p=\langle 1,0\rangle$. Now, the composition $RT\phi$ fixes both $O$ and $p$! All that remains is to think about where $q$ has been sent.

Since $RT\phi$ is an isometry it preserves distances, so it must send $q$ to a point which is unit distance from $O$ and $p$ (remember - it send $O$ and $p$ to themselves)!

The isometry $RT\phi$ fixes the both $O$ and $p$, so there are only two options on where it sends $q$. Here we see the case where it does *not* get sent directly to $q$.

There are only two such points in the plane, which lie at the intersections of the cirlces \[x^2+y^2=1\hspace{1cm}(x-1)^2+y^2=1\] The two options are either $q$ itself - $(\tfrac{1}{2},\tfrac{\sqrt{3}}{2})$ or the same point with the $y$-coordinate negated. So, let $F$ be the following isometry: its the identity if $RF\phi(q)$ was already equal to $q$, and is the reflection in the $x$ axis otherwise.

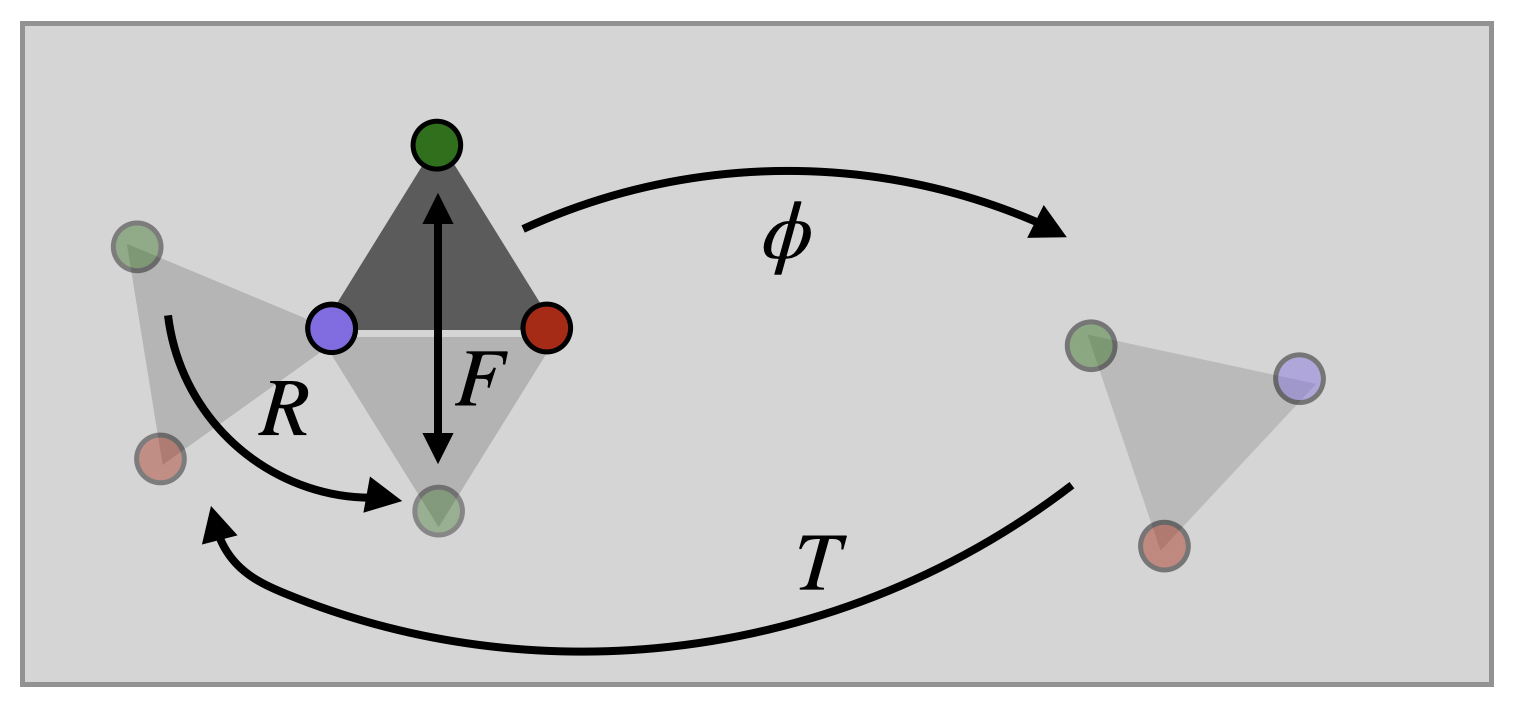
Composing $RT\phi$ with a flip $F$ across the $x$ axis creates an isometry that fixes all of $O$, $p$ and $q$.

Now, we have the map $FRT\phi\colon\EE^2\to\EE^2$, which fixes all three points of the equilateral triangle! This is the same thing the identity map does on these three points, so by Corollary 13.2 this must actually be the identity!

\[FRT\phi = \mathrm{id}\]

One by one composing with the inverses of the maps we’ve added on, we can now solve for $\phi$:

\[\phi= T^{-1}R^{-1}F^{-1}\]

Since the inverse of a translation is just another translation, the inverse of a rotation is another rotation, and the inverse of a reflection is another reflection (its the same reflection, actually!) we see $\phi$ is a composition of translation, rotation and reflection as claimed.

Thus - every isometry is built from the building blocks we already know of: there are no new mystery isometries out there to be discovered! This is a powerful fact as it lets us claim things about all isometries by just checking them with rotaitons, translations, and reflections. For example:

Corollary 13.3 (Isometries are Affine Maps) All Euclidean isometries are affine maps of the plane.

Proof. Let $\phi$ be an arbitrary Euclidean isometry. By Theorem 13.2, we may write $\phi=TRF$ for $T$ a translation, $R$ a rotation about the origin, and $F(x,y)=(x,\pm y)$ either a flip across the $x$ axis or the identity. Thus, the proof is just a direct computation: a rotation about the origin is given by a linear map (Theorem 11.4) so \[RF(x,y)=\pmat{u&-v\\ v&u}\pmat{x\\ \pm y}=\pmat{ux\pm vy\\ -vx\pm uy}\] Next, any translation is an affine map of the form $T(x,y)=(x+a,y+b)$ So

\[\phi(x,y)=TRF(x,y)=T\pmat{ux\pm vy\\ -vx\pm uy}=\pmat{ux\pm vy+a\\ -vx\pm uy+b}\]

Each of these components is an affine function, so the entire isometry $\phi$ is affine.

13.4 Conic Sections

Though greek geometry lacked the ability to deal with general curves, they did know quite a lot about a specific family of curves called conic sections These include the circles and lines we have already discussed, but also parabolas, ellipses, and hyperbolas. We will not spend much time on them here, except to show how our new formalism lets us come up with precise equations for these curves much as it did for lines and circles already.

Remark 13.2. These curves are called conic sections because we can alterantively define them as the possible curves one can get by slicing a 3-dimensional cone by a plane at different angles.

13.4.1 Parabolas

A geometric definition of the parabola dating back to ancient greece is that it is the set of points which lie at an equal distance from a given point and line in the plane. More precisely

Definition 13.3 Let $L$ be a line (called the directrix), and $f$ a point not on that line (called the focus). The parabola $P$ with directrix $L$ and focus $f$ is the set of points $(x,y)$ which lie at the same distance from $\ell$ as they do from $f$: \[\dist((x,y),L)=\dist((x,y),p)\]

Recall that the distance to a line $L$ is defined as the shortest distance between $(x,y)$ and any point on $L$ (Definition 12.8).

A parabola is the set of points which are the same distance from a point (the focus) and a line (the directrix). In this figure, line segments of the same color are supposed to be the same length.

Exercise 13.7 Let $L$ be the $x$-axis, and $f$ the point $(0,2)$ along the $y$-axis. Find an equation that points $(x,y)$ on the parabola determined by $L$ and $f$ must satisfy.

Exercise 13.8 In this problem we confirm that $y=x^2$ is indeed a parabola! Let $L$ be a horizontal line intersecting the $y-$axis at some point $(0,-\ell)$, and $f=(0,h)$ be a point along the $y$-axis for $\ell,h>0$.

Write down an algebraic equation for the coorddinates of a point $(x,y)$ determining when it is on the parabola with focus $f$ and directrix $L$.
Find which point $f$ and line $L$ make this parabola have the algebraic equation $y=x^2$.

13.4.2 Ellipses & Hyperbolas

Ellipses and hyperbolas are also defined by a condition involving distance. Instead of distance from a single point (circles) or distances between a point and a line (parabolas), these shapes involve the distances from a pair of points.

Definition 13.4 Let $f_1$ and $f_2$ be two points in the plane (called focii), and $d$ a number (called the distance sum). The ellipse with focii $f_1,f_2$ and distance sum $d$ is the set of points $p=(x,y)$ in the plane where \[\dist(p,f_1)+\dist(p,f_2) = d\]

An ellipse is the set of points where the sum of distances to two points is constant. Here, $p$ and $q$ are both on the ellipse as the lengths of the green and blue polygonal segments are equal.

Exercise 13.9 Find an equation of the form $ax^2+by^2=c$ determining when a point lies on the ellipse with focii $(1,0)$ and $(-1,0)$ with distance sum 4.

A hyperbola is defined similarly, except it is a difference of distances instead of a sum:

Definition 13.5 Let $f_1$ and $f_2$ be two points in the plane (called focii), and $d$ a number (called the distance difference). The hyperbola with focii $f_1,f_2$ and distance sum $d$ is the set of points $p=(x,y)$ in the plane where \[|\dist(p,f_1)-\dist(p,f_2)|= d\]

This distance difference may be positive or negative (hence the absolute value). Each sign determines one branch of the hyperbola - its a disconnected curve with two components!

An hyperbola is the set of points where the differece of distances to two points is constant. Here, $p$ and $q$ are both on the hyperbola as the difference between the lengths of the green segments equals the difference between the blue segments.

Exercise 13.10 Prove that the equation $y^2-x^2=1$ determines a hyperbola. What are the two focii? What’s the distance difference?

13.4.3 Equidistants to a Line

This is not itself a conic section, but like the previous shapes we’ve discussed fits into the class of “shapes defined by a distance constraint.”” A circle is the set of points which are equidistant from a point (its center). One could attempt to generalize this notion by replacing the point at the center with something more general, and measuring

The most reasonable “generalized center” to consider first is a line: it is the only other shape we know so far, after all! What curves are equidistant to a line? In fact, the answer here is not that interesting: its just a pair of two lines.

Proposition 13.3 Given a line $L$, the set of points lying at distance $d$ from $L$ are two disjoint lines.

Proof. Let $L$ be a line, and choose an isometry $\phi$ that moves $L$ to the $x$-axis (which we will denote $X$). Now the distance from a point $p=(a,b)$ to a point $(x,0)$ on $X$ is $\sqrt{(x-a)^2+b^2}$, which is minimized when $x=a$: thus \[\dist((a,b),X)=\sqrt{b^2}=|b|\]

Thus, the set of points at distance $r$ from $X$ contains all pairs $(x,r)$ and $(x,-r)$ for any $x$: these are two lines \[L_+(x)=(x,r)\hspace{1cm}L_-(x)=(x,-r)\] To solve the original problem, we apply the inverse isometry $\phi$ taking $X$ back to the line $L$. Since isometries take lines to lines and preserve distance, this takes $L_{\pm}$ to two lines, each at distance $r$ from $L$ as claimed.

However, we include brief mention of this fact for two reasons. One, in a lost work of Archimedes, On Parallel Lines, it seems that he tried to work with alternative definitions of parallelism based on this fact, to simplify Euclids theory. Below is a quote from Boris Rosenfeld’s A History of Non-euclidean Geometry:

It seems that the first work devoted to this question [the theory of parallels] was Archimedes’ lost treatise On parallel lines which appeared a few decades after Euclid’s Elements. […] it is very likely that Archimedes used a definition of parallel lines different from Euclid’s. […] it is possible that Archimedes based his definition of parallel lines on distance.

And secondly, while we found here that the equidistant curves to a line are just another pair of lines, this fact (as presciently investigated by Archimedes) is actually equivalent to the parallel postulate, and so will be false in the other geometries we study! Thus, we will reference this short section in those future geometries, to contrast our new discoveries with the old.