30 Geometry of Minkowski Space
Our introduction to Minkowski space in the last chapter essentially provided a playground for us geometers,
- We got to try out our definitions (of isometries, distances, etc) in an unfamiliar context, which was still quite close to things we’ve seen before (all we switched was one negative sign in the dot product!)
- We were able to use our geometric skills to discover a new model of hyperbolic geometry living inside this world!
This provides a nice end to our story of hyperbolic space, and our approach to geometry as a whole. But it also serves as the beginning to a new and wonderful story of geometry and its interaction with physics. In these final chapters we endeavour to tell a small bit of this story, where Minkowski space itself (and not merely the hyperboloid lying within it) takes center stage.
To begin, we need to take a deeper dive into the geometric properties of Minkowski space.
30.1 Positive and Negative
As a geometry, Minkowski space is a
At each point
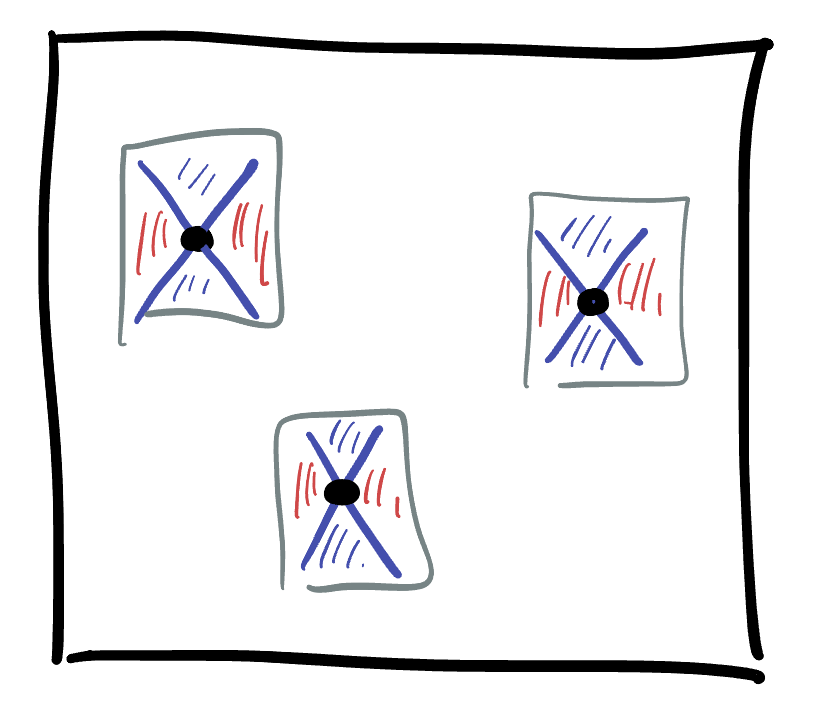
One of the most effective ways to study a geometric space is with curves: for example, in Riemannian geometry we used curves to help us define geodesics, and then learned a ton of geometry from trying to classify geodesics. Let’s attempt the same here.
First, we recall the definition of a regular curve. In Riemannian geometry, we said this is a curve
Definition 30.1 (Regular Curve:) A curve
However note here that
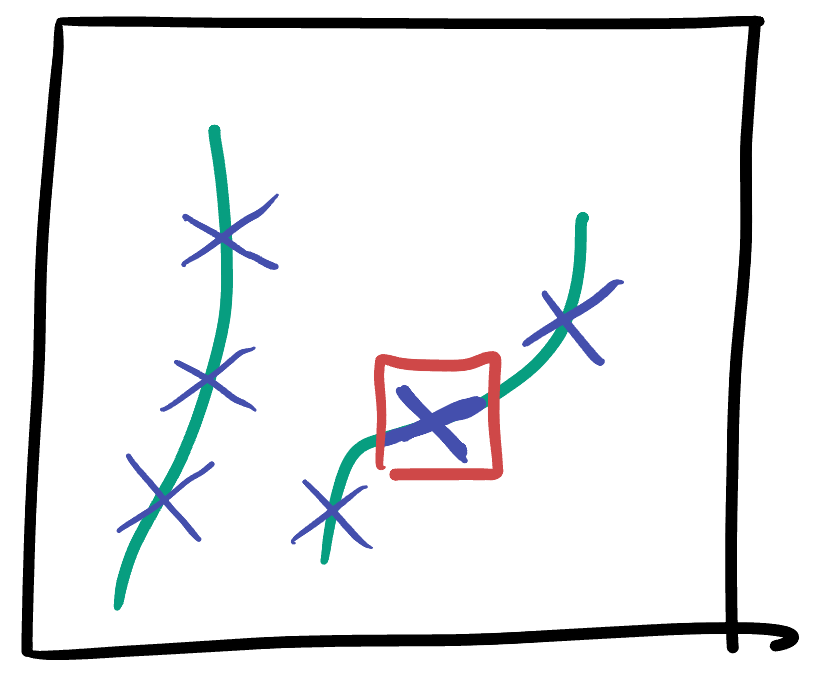
This condition makes the collection of regular curves in Minkowski space quite different than in Riemannian geometry: we can sort all regular curves into two classes (which for now, we will call positive and negative).
Definition 30.2 (Positive and Negative Curves.) We say a regular curve is positive if
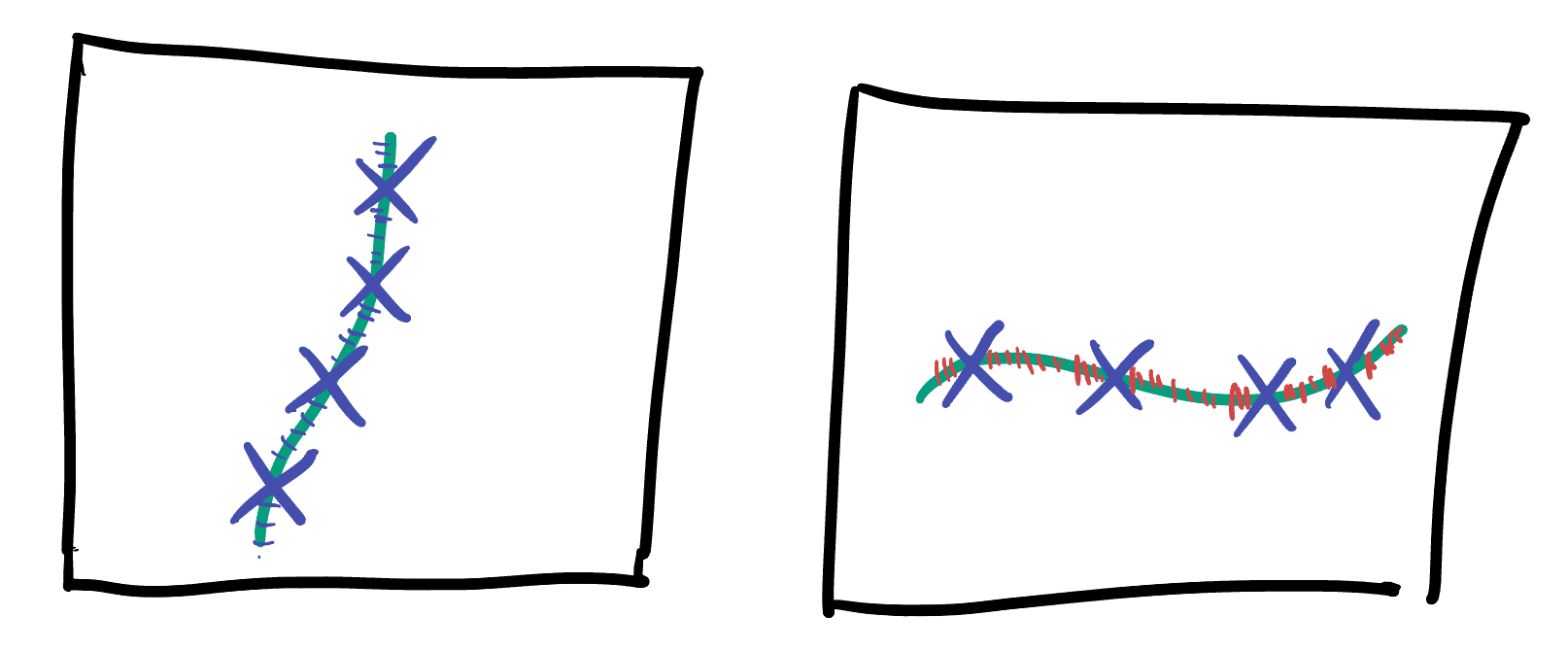
Theorem 30.1 Regular Curves are Either Positive or Negative. Precisely, let
Proof. Apply the intermediate value theorem to the function
Of the non-regular curves, most have points of positive and negative norm - but a few special ones do not: they have zero norm everywhere. These are worthy of a special name
Definition 30.3 A curve
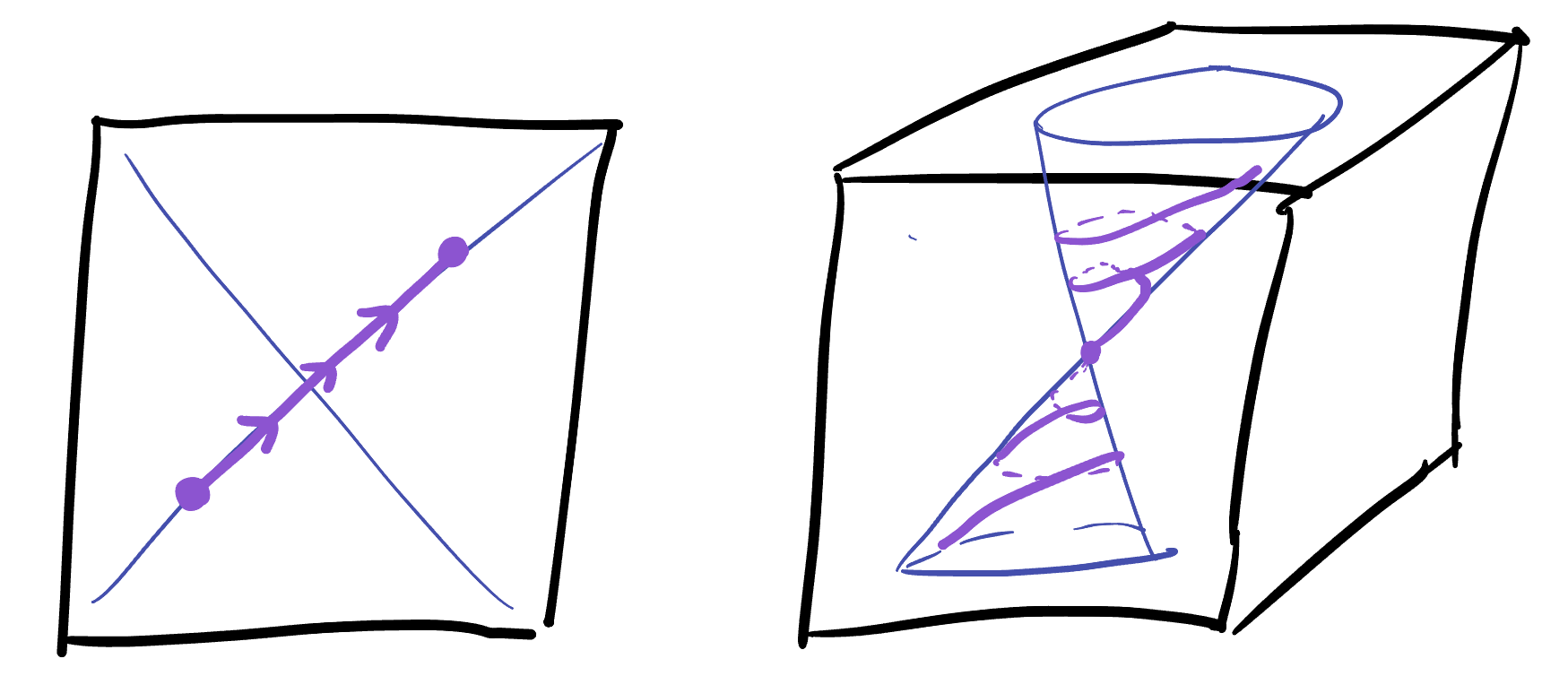
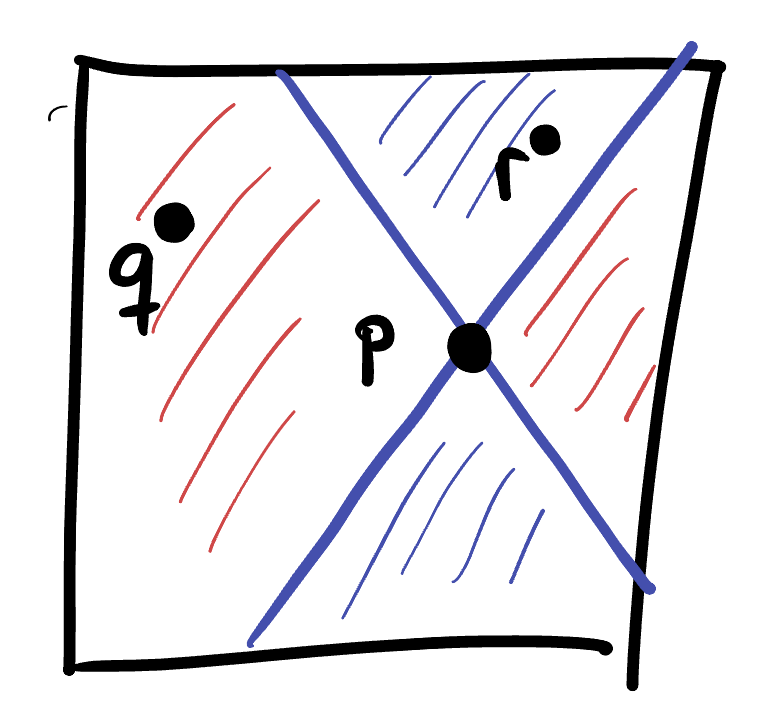
This sorting of all regular curves curves into two classes has profound implications: it let’s us actually sort the points of
Definition 30.4 (Positive and Negative Pairs of Points.) Let
This definition requires some checking to be sure its well-defined:
Theorem 30.2 If two points are connected by a negative curve, then any regular curve connecting them must be negative. Same for positive pairs. Hint: A sneaky use of Rolle’s theorem to the z coordinate, for negative curves!
Using affine lines (which are easy to tell when they are positive or negative curves, just using the norm of their derivative) we can sort points into positives and negatives with this definition.
Exercise 30.1 For the origin, show that the points that are positively separated from
This same thing holds true at every point: given a point
30.1.1 Geodesics
Now that we understand a bit of isometries, regular curves, and positively/negatively separated points, we can start to talk about geodesics in Minkowski space. This discussion is more subtle than in Riemannian geometry, for several reasons.
We’ve already dealt with one major difference: the fact that not all pairs of points in Minkowski space are created equal - for some pairs, every regular curve connecting them is a positive curve, and for others every regular curve is a negative curve (and finally, for the remaining pairs of null-separated points, there are no regular curves at all joining them).
Thus, we already expect there to be two notions of geodesic, a positive geodesic as some optimization problem over the space of positive curves, and correspondingly a negative geodesic for pairs of negatively separated points.
But there’s one more subtlety to confront: we already know that Minkowski space has curves of total length zero between distinct points. This radically different behavior that Euclidean space suggests a potential problem with our usual notion of geodesic as minimizing - if we can make a regular curve nearby to a curve of zero length, we might expect that regular curve to have a very short length - and perhaps taking the infimum over all regular curve lengths actually gives zero, which is not realized by any regular curve.In fact, exactly this worry happens.
Theorem 30.3 (A truly mindbending example) Consider the following two curves in
Which is longer? Now do the same for the piecewise curve that bends at the point
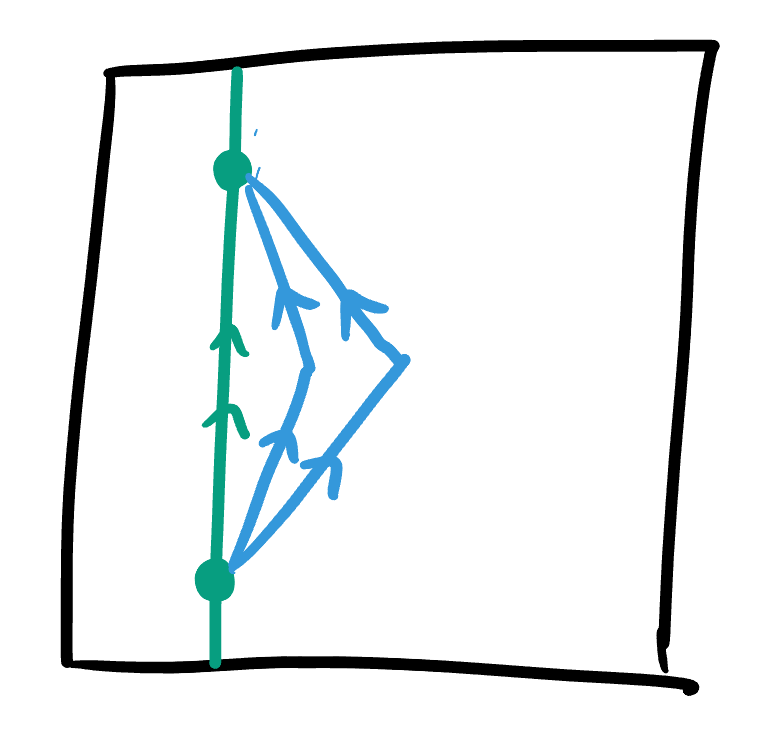
Exercise 30.2 Can you construct a similar example, for a pair of positively separated points?
One concern here might be that these curves described are not regular - they have a corner (they are piecewise regular, however). This is not actually a technical concern as it is fine (and often more convenient) to just work with the class of piecewise regular curves from the start. But even if you choose not to do so, these examples still point the way:
Example 30.1 Given two negatively separated points (without loss of generality we can take them to be

The situation is even worse that these examples make it appear - here we found curves that were very short, but were also very far away from our original curve. Perhaps one might hope there aren’t any actually nearby to our original curve - so maybe its still “locally” nice. But this intuition is rather shaky; by modifying the idea above to introduce lots of small crinkles instead of one big deviation….
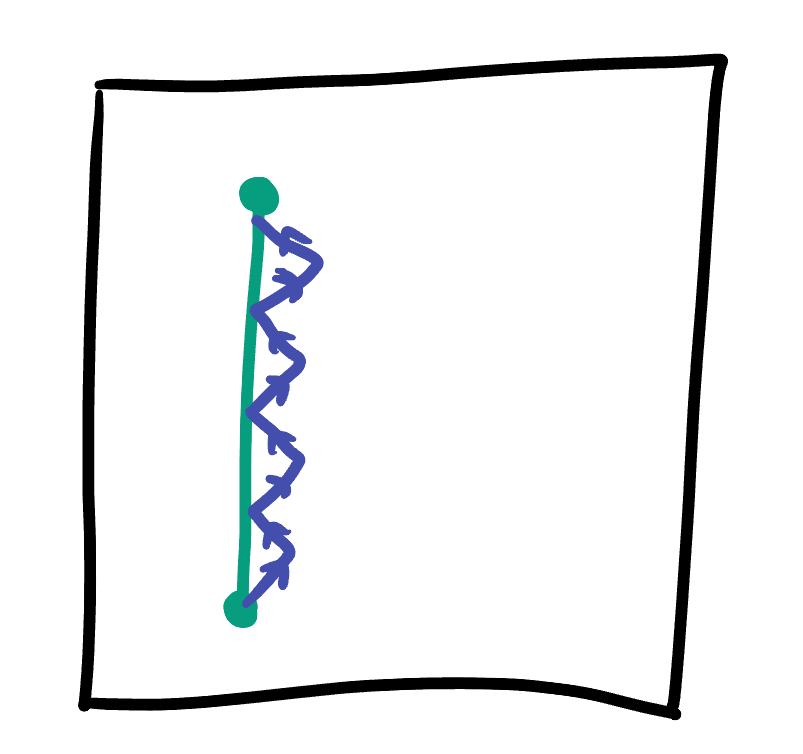
Exercise 30.3 If you constrain a curve to never get more than
What about if its a regular curve?
Corollary 30.1 There are no length minimizing regular curves in Minkowski space: given any pair of positively or negatively separated points, the infimum of the lengths of all regular curves joining them is zero, but there is no regular curve of length zero joining them.
Thus, the inifmum is not a minimum, so the minimum does not exist!
This example teaches us two important things: first the formal definition of geodesic can’t be directly borrowed from Riemannian geometry, but secondly we can see its clearly not even the right notion! In Riemannian geometry, its easy to make a curve longer, by wiggling it, curves of minimal length are the right sort of optimal objects to seek. But in Minkowski space, its easy to make a curve shorter by wiggling it; and in fact, its difficult to make a curve longer! Almost everything you try shortens it…so perhaps the right thing to do is turn our intuition on its head and define our optimal objects as the length maximizing curves. Amazingly, for negative curves this works!
Definition 30.5 (Negative Geodesics) Let
We call this curve the geodesic from
This is a definition that justifies itself with a claim: (that there is a maximum, and as a bonus its unique!) So, we should check this!
Theorem 30.4 If
Proof. Without loss of generality we can take our points to be
Where the last equality follows as since
But, no matter what
Both sides of this are positive and the square root is an increasing function, so this implies
and finally,
The first integral here is none other than the length of
Thus for any such curve
As a corollary of this, looking closer at the argument above we can see that in fact no other curve can be as long as
Exercise 30.4 Geodesics connecting negatively separated points are unique.
Hint: if
In fact, there’s a way to make this craziness sound not so strange after all. Remember that we defined infinitesimal arclength by using an absolute value for negative curves, since the dot product yields a negative number. So, finding the maximal length is really finding the maximum absolute value which is the same as finding the most negative (since we know the original numbers are all negative). But the most negative is the minimum! So, we could simply modify our definition of the length of a negative curve to remember that the dot product is negative
And with this new definition all curves have negative length, the maximum is not achieved (as curves can have lengths arbitrarily close to zero) but the minimum is: curves of minimal length are again geodesics! This is a totally fine approach to take, and perhaps a convenient one if you are very good at not missing minus signs. However when it comes to our use case for Minkowski geometry (the physics of relativity) we will see that the length of negative curves really corresponds to time intervals, and if we put a negative here, we’ll have to negate it once more to think of intervals of time as positive like we do in daily life. So, we will opt not to do this, and instead just deal with the fact that geodesics are maximizing.
This turns out to be alright actually - as its strangeness actually forces us to think carefully about what is going on, and this careful though reveals things are even stranger for positively separated points!
In
Exercise 30.5 Let
- Show that there are nearby curves to
- Show that there are nearby curves to
To study this a bit further, it will be useful to have a little more terminology available to us, so we introduce the idea of a variation:
Definition 30.6 If
We call
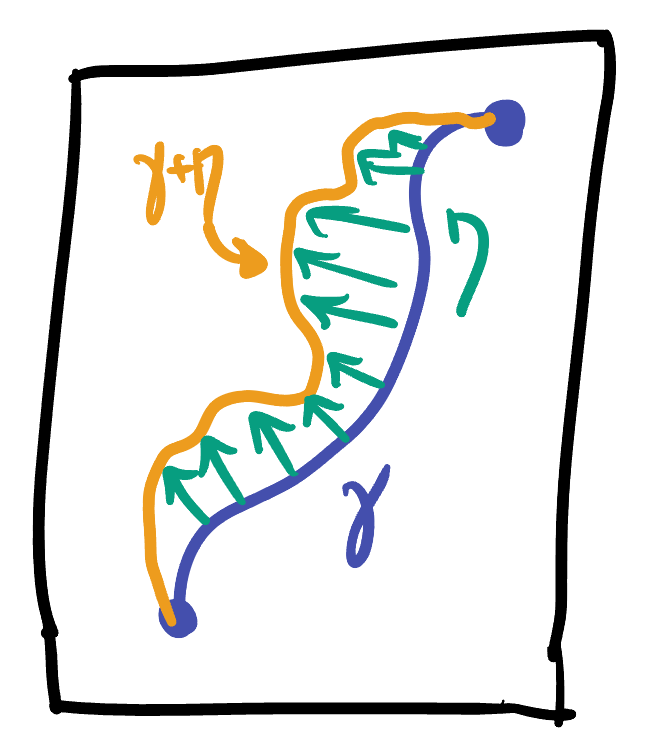
Exercise 30.6 Let
- Show that
- Show that
This shows that
Theorem 30.5 Let
We do not prove this theorem, as understanding the precise definition of a saddle point in infinite dimensions, and ensuring to do the calculation correctly would take us rather far afield. And, seeing that we will never use this result (in our upcoming physics application, it will turn out that only the negative curves are relevant) its just not worth it here.
However, it does tell us that if we want a general definition of geodesic in Minkowski space, we need to work a little harder: we can’t just replace local minimum with local maximum and call it a day; instead we should seek a definition which captures both max/mins and saddles.
Definition 30.7 (Minkowski Geodesics) A minkowski geodesic is a regular curve
In fact, one could take this more general definition and apply it back in Riemannian geometry as well. Even though it appears to allow for more possible behaviors, one can prove that with a positive inner product at each tangent space, the only critical points of length are actually minima - that is, they are the same geodesics we have already found! So, there is no harm in replacing the definition with this, and using it universally across both Riemannian and Minkowski spaces.
This small change turns out to be the a hint to much wider generalizations, bringing geometry deep into the study of quite a lot of fields of math and physics. We do not have the time nor background to develop such here, and should remain focused on our goal. But I cannot help but mention one: Lagrange managed to rewrite the laws of classical mechanics as an optimization problem, where the solutions to Newton’s laws appeared to correspond to the minima of a certain function (called the Action Functional). But on closer inspection - this didn’t always work! Instead we discovered physics is not seeking minima but rather critical points and so this generalized notion of geodesic is the correct notion here as well. (Look up The Principle of Stationary Action to learn more)