$$ \newcommand{\RR}{\mathbb{R}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\CC}{\mathbb{C}} \newcommand{\NN}{\mathbb{N}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\EE}{\mathbb{E}} \newcommand{\HH}{\mathbb{H}} \renewcommand{\SS}{\mathbb{S}} \newcommand{\DD}{\mathbb{D}} \newcommand{\pp}{^{\prime\prime}} \newcommand{\p}{^\prime} \newcommand{\proj}{\operatorname{proj}} \newcommand{\area}{\operatorname{area}} \newcommand{\len}{\operatorname{length}} \newcommand{\acc}{\operatorname{acc}} \newcommand{\ang}{\sphericalangle} \newcommand{\map}{\mathrm{map}} \newcommand{\SO}{\operatorname{SO}} \newcommand{\dist}{\operatorname{dist}} \newcommand{\length}{\operatorname{length}} \newcommand{\uppersum}[1]{{\textstyle\sum^+_{#1}}} \newcommand{\lowersum}[1]{{\textstyle\sum^-_{#1}}} \newcommand{\upperint}[1]{{\textstyle\smallint^+_{#1}}} \newcommand{\lowerint}[1]{{\textstyle\smallint^-_{#1}}} \newcommand{\rsum}[1]{{\textstyle\sum_{#1}}} \newcommand{\partitions}[1]{\mathcal{P}_{#1}} \newcommand{\erf}{\operatorname{erf}} \newcommand{\pmat}[1]{\begin{pmatrix}#1\end{pmatrix}} \newcommand{\smat}[1]{\left(\begin{smallmatrix}#1\end{smallmatrix}\right)} $$

1 Euclid

Geometry began deep in antiquity, arising from our need to measure properties of the physical world as we came out of the last ice age and began to collect ourselves into cities. Much of the subject’s long prehistory is lost to the depths of preliterate time, but signs of the ancients knowledge remain in their surviving artworks.

An Archimedean spiral on Neolithic Pottery, Romania 7000BCE

With writing and the ensuing civilization growth, recognizably modern geometry was practiced by bronze-age peoples the world over, with notable examples in Babylon, Egypt and China.

A collection of Babylonian homework exercises, written in Akkadian, 1700BCE

Geometry at this stage in our history was more a compendium of true facts about space, than it was a coherent theory of how space behaved. One could derive new facts from known facts, or see that new observations were consistent with existing knowledge, but early mathematicians had not yet found an order to this chaos.

1.1 Euclid’s Postulates

By the time Euclid was born in the 300s BCE, Greek civilization was reaching the twilight of its golden age, and serious geometry had been practiced by its mathematician-philosophers for centuries. While not much is known of Euclid’s personal life, his fame survives into modernity as the author of the three book series The Elements, collecting and systematizing much of the Greek’s knowledge of geometry. Much of its content originates from earlier mathematicians, including Eudoxus, Hippocrates of Chios, Thales and Theaetetus, while other theorems in The Elements are previously mentioned by Plato and Aristotle.

But this is not to take anything away from Euclid’s incredible achievement: while the theorems were not all original, it is his exposition that became a model for all mathematics written over the following twenty centuries. Euclid took the mass of knowlege humans had discovered, and built it into a logical, self-contained, and understandable body of knowledge. He turned a collection of truths into a mathematical theory.

Euclid reduced the entirety of Greek geometry to the logical consequences of just five statements. Five! Everything that had ever been measured about the nature of space sprung forth from pure logic and five basic truths. These truths, which Euclid called his Αξιώματα (Axiomata), we usually call Euclid’s Postulates in English.

Definition 1.1 (Αξιώματα του Ευκλείδη: Euclid’s Postulates)

Η κατασκευή μιας ευθείας γραμμής από ένα σημείο σε οποιοδήποτε άλλο
Μια πεπερασμένη ευθεία μπορεί να επεκταθεί απεριόριστα
Ένας κύκλος ορίζεται από ένα κέντρο και μια απόσταση(ακτίνα)
Όλες οι ορθές γωνίες είναι ίσες
Έστω δύο ευθείες που τέμνονται με μια τρίτη. Οι ευθείες αυτές θα έχουν ένα σημείο τομής από την μεριά που οι εσωτερικές γωνίες που σχηματίζονται με την τρίτη ευθεία έχουν άθροισμα μικρότερο από δύο ορθές γωνίες.

In English:

A straight line segment can be drawn joining any two points.
Any straight line segment can be extended indefinitely in a straight line.
Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
All right angles are congruent.
If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.

These five statements were chosen to be as directly observable and intuitive as possible: and for the most part they do an excellent job at that. Drawing a line between any two points? Sounds reasonable. Making a line longer? Also reasonable. Rotating any line segment around to make a circle? Alright. Any two right angles being congruent? Of course.

But the fifth one, that one you have to read a couple times and draw a picture before you’re convinced of its truth. We will have much more to say about this 5th postulate in the next chapter.

1.2 The Idea of Proof

The real power of Euclid’s postulates comes from the ability to prove things from them.

Definition 1.2 (Proof) A proof of a statement $S$ is a sequence of logical claims, starting from a collection of foundational statements (like a list of axioms and previously proven statments) and ending with the statement $S$ that you wanted to verify is true.

As a quick example, if we take as foundational the definition of even number being a integer that is $2$ times another integer and the rules of arithmetic, we can prove that for any integer $x$, the integer $x+x$ is even. Our proof goes as follows:

We can use the fact that $1x=x$ to rewrite $x+x$ as $1x+1x$.
We can factor out the $x$ to get $1x+1x=(1+1)x$
We can use that $1+1=2$ to get $(1+1)x=2x$
$2x$ is twice the integer $x$, so it is even.
Thus, since $x+x=2x$, we see $x+x$ is even.

This proof is not particularly exciting, but it is clear and unambiguously true. Each bit of the proof made just a small step at a time, and explained why each step held using the foundational material. Anyone who understands the foundational material and knows how to read would be convinced by this argument that $x+x$ must be even.

Arguments in greek geometry are exactly of the same style, except we replace the rules of arithmetic with the Postulates of Euclid, and definitions like “evenness” with geometric definitions like “triangle”.

Definition 1.3 (Triangle) A triangle is a figure in the plane composed of three points $p,q,r$ which do not all lie on a common line. The sides of the triangle are the line segments $pq$, $pr$ and $qr$. The angles of the triangle are defined by these sides at the points $p,q,r$ themselves.

Indeed, given just this definition and the five postulates of Euclid, we can follow him in proving his first Proposition

Theorem 1.1 (Equilateral Triangles Exist: Elements Prop I) There exists a triangle in the plane all of whose sides are the same length.

Proof.

Choose two points $p,q$ in the plane. Draw the line segment between them, of length $L$. (Postulate 1)
Now form the circle of radius $L$ centered at $p$, and the circle of radius $L$ centered at $q$ (Postulate 3)
These two circles intersect in two points. Select one of the intersection points, call it $r$.
Use postulate 1 again to draw a line from $p$ to $r$ and from $q$ to $r$. Together with the original line, these form a triangle.
The line segment from $p$ to $r$ is length $L$, as is the length of the segment from $q$ to $r$ as they are both radii of circles. But the distance from $p$ to $q$ was $L$ too: so this triangle has three sides of length $L$.

Remark 1.1. That the circles intersect seems intuitively obvious, but how would one actually prove this? This is the beginning hints that defining things in terms of calculus will prove useful. From our modern perspective, this seems to have something to do with the continuity of the circle, and perhaps the intermediate value theorem.

A video demonstration of this proof is below:

Propositions, themselves being verified from the list of known facts, are then “legal” to be used in the justification of future facts. Euclid is very intentional in his development of the subject, and makes sure that every proposition only uses in its justification facts that have been previously proven.

1.3 Absolute Geometry

Euclid delays using Postulate 5 as long as possible, and proves the first 28 propositions of Book I using only Postulates 1-4. (Indeed, in Proposition I we used only Postulates 1 and 3!) These days, we call such results theorems of absolute geometry.

Definition 1.4 (Absolute geometry) Absolute geometry is the set of theorems which can be proven using only Euclid’s postulates 1 through 4.

Below we embark on a brief, and incomplete tour of Euclid’s work in absolute geometry to get better acquainted with the Greek notion of geometric proof.

The early propositions focus mostly on increasing our toolkit: they prove that its possible to do certain useful geometric constructions from the axioms, so that we can in the future use these directly where convenient.

Proposition 1.1 (Copying a Line Segment: Elements Prop 2) Given a segment $L$ and a point $p$ not on that line, its possible to draw a new line segment starting at $p$ whose length is the same as $L$.

The proof of this proposition uses only Proposition I together with the 5 postulates, and so must be quite ingenious: there isn’t much to work with! Indeed, its best understood through an animation, so there is a youtube video below.

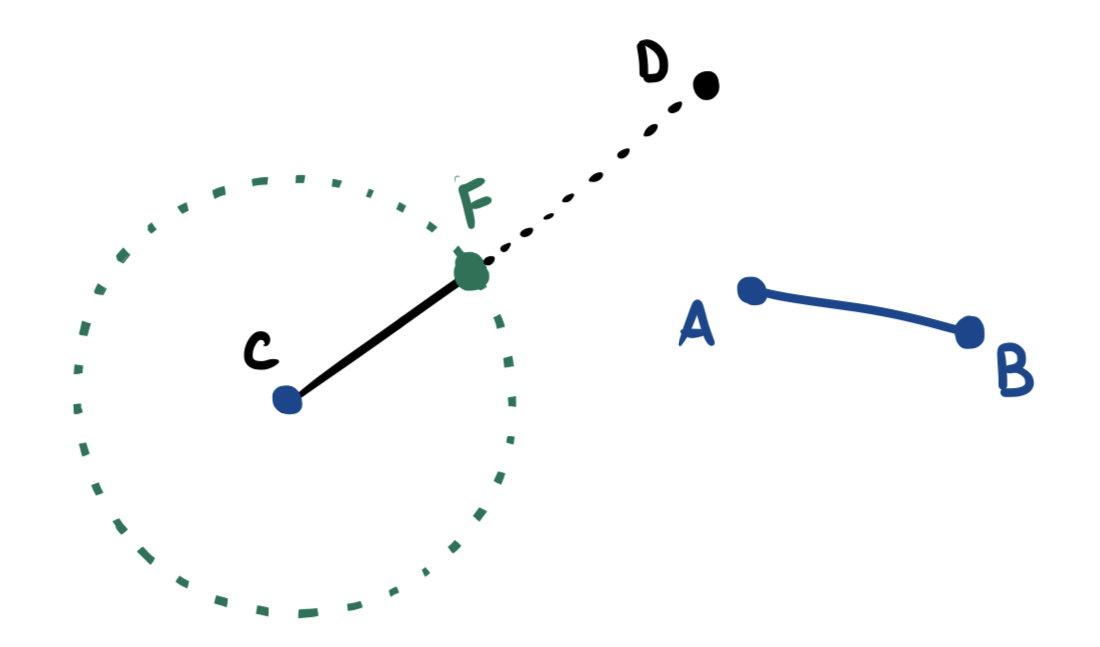
Proposition 1.2 (Cutting a Line Segment to Size: Elements Prop 3) Given two line segments of unequal lengths, its possible to cut the longer line segment so that the remaining piece has the same length as the shorter.

Proof. Start with a line segment $AB$, and another line segment $CD$, and without loss of generality let’s say that $CD$ is the longer segment.

Use Proposition 2 to build a segment with the same length as $AB$ but now starting at the point $C$.
Now use Postulate 3 to spin this new line around to form a circle centered at $C$.

This new line intersects $CD$ in a new point, call it $F$.
Now the line $CF$ is a radius of the circle, and so has the same length as the original copied segment: the length of $AB$.

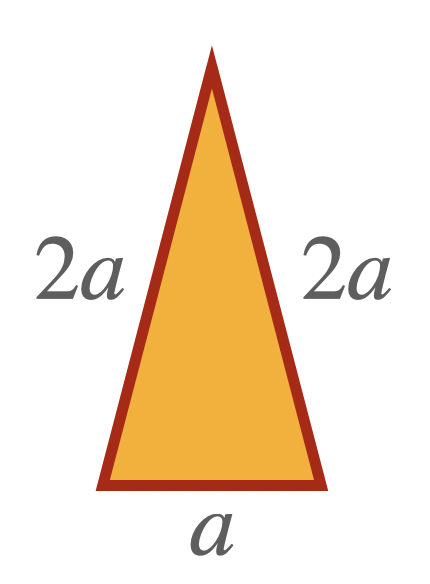
Exercise 1.1 (Constructing an Isoceles Triangle) Start with a line segment of length $a$. Prove that you can construct a triangle with one side of length $a$, and two sides of length $2a$, using the postulates 1-5 and the propositons 1-3 given so far.

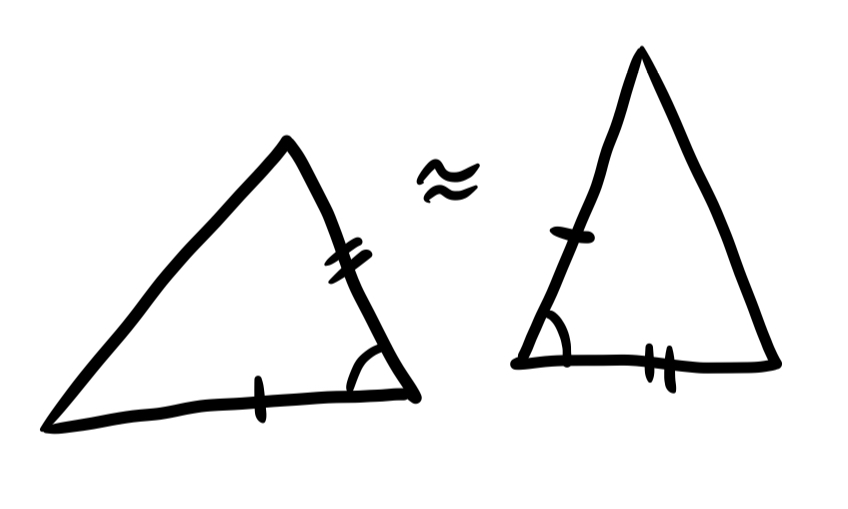
An isosceles triangle with two sides double the other.

Now that we can copy and cut line segments, Euclid is ready to prove his first theorem about telling when two shapes are the same (or congruent). You may recall this as side-angle-side congruence from elementary geometry: Euclid proves it by using what we just proved to copy one triangle on top the other, to see they are equal.

Theorem 1.2 (Side-Angle-Side Congruence: Elements Prop 4) If two triangles share a pair of sides with the same lengths, and those sides form an angle of equal measure on each, then the two triangles are congruent.

Side-Angle-Side Congruence: sides with the same length and angles with the same measure are marked alike on the two triangles.

Euclid continues on this way for some time, proving more theorems theorems about triangles, including side-side-side congruence.

Theorem 1.3 (Side-Side-Side Congruence: Elements Prop 8) If two triangles have corresponding sides of the same three lengths, then the two triangles are congruent.

Side-Side-Side Congruence: sides with the same length are marked alike on the two triangles.

As a quick application we use this to show that the angles of an equilateral triangle are all equal to one another.

Proposition 1.3 The three angles of an equilateral triangle are equal.

Proof. Let $ABC$ be an equilateral triangle. Then as all of its sides are the same length, it is side-side-side congruent to any rotated copy of itself. Concretely, we see that $ABC$ is congruent to $BCA$.

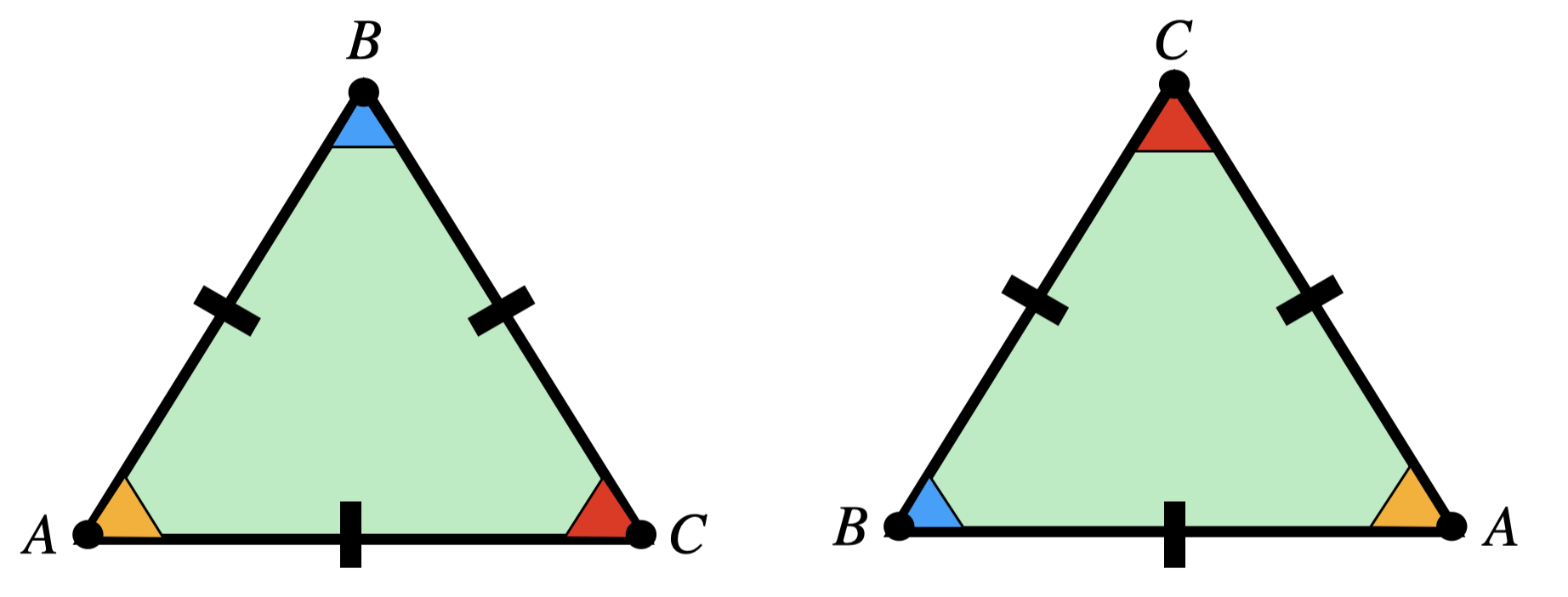
Equilateral triangles have three equal angles.

This sets up an equality between the angles: \[ A=B\hspace{0.5cm} B=C\hspace{0.5cm} C=A\] Thus all the angles are equal to one another.

These congruences are both theorems of absolute geometry, meaning that they are true in any world where Postulates 1-4 hold. Being able to tell when two triangles are the same gives Euclid a new power - to verify that one can cut an angle precisely in half.

Proposition 1.4 (Bisecting an Angle: Elements Prop 9) If $\theta$ is any angle, it is possible to draw a line dividing it into two angles each of measure $\theta/2$.

Before watching the video on this one (or looking back at your notes) try to draw the diagram from the instructions!

Proof.

Start with an arbitrary angle at a point $A$, and choose a point along $D$ one of the angle’s rays.
Use the segment from $A$ to $D$, with Postulate 3, to construct a circle centered at $A$.
This circle intersects the angles other ray at some third point, $E$
Use Proposition 1 to construct an equilateral triangle on the segment $DE$, which goes across the angle.
Call the vertex of the equilateral triangle $F$. Now use Postulate 1 to draw a line from the angle’s vertex $A$ to $F$.
This creates two triangles, using the new line $AF$, and then using one side of the equilateral triangle, and one side ray of the original angle.
These two triangles, $AEF$ and $ADF$ have all three pairs of sides the same length: thus, by Side-Side-Side congruence, they are equal.
This means their angles are also equal. So the two angles we have split the original angle at $A$ into are equal, and so each must be half the original angle’s measure.

This proof is a bit involved too - so it may be helpful to watch a video for future reference!

Applying this to a straight angle allows one to bisect this into two equal angles. Since half a straight angle is a right angle, a corollary of this propositon is that it is possible to construct a right angle along any line segment.

Proposition 1.5 (Constructing Right Angle: Elements Prop 11) Given a line segment $L$ and any point $p$ along that line segment, it is possible to construct a perpendicular line $T$ to $L$ passing through $p$.

At this point, we now (finally!) know that right angles must exist! Of course we had an axiom about right angles, but it did not tell us that there were any: it just said IF you had two right angles, then they are congruent. But it never gave you a means of making a right angle yourself! Now that we have one, we can do several interesting constructions: for example, we can prove that right triangles exist:

Proposition 1.6 A right triangle exists can be created with any two leg lengths $a,b$.

Proof. Begin with a line segment $S_1$ of length $a$, and another line of length $b$.

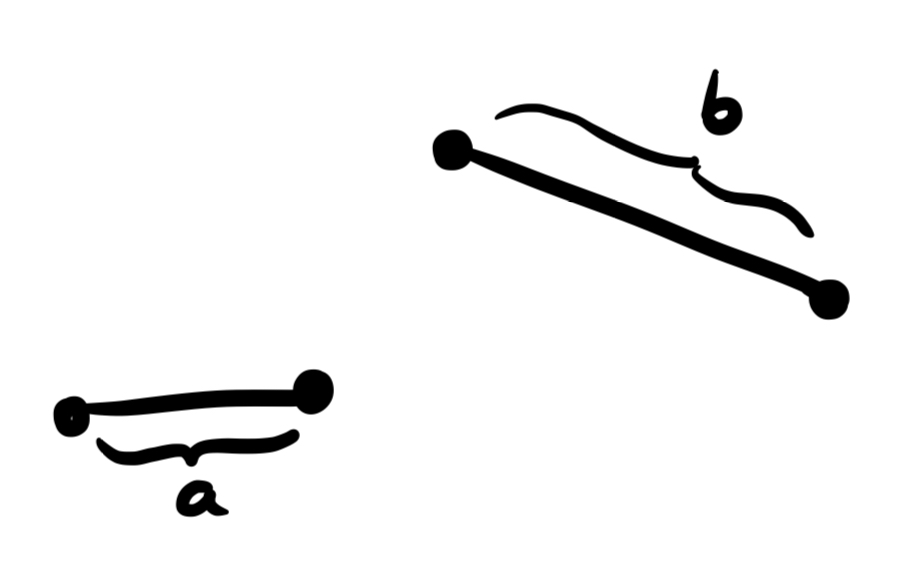
Lines of the lengths we want as legs of the right triangle.

Using Proposition 1.5, construct a segment at a right angle to $S_1$ at one of its endpoints, $p$.
Use postulate 2 to extend this line segment indefinitely (in case the original segment you constructed was shorter than $b$!)

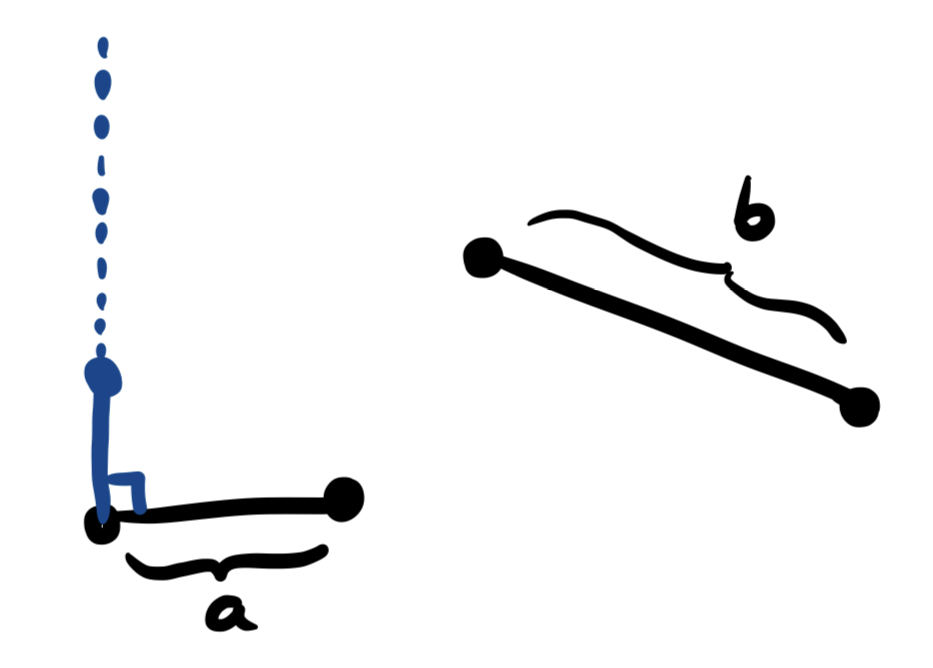
Constructing a long perpendicular to one segment.

Use Euclid’s Proposition 3 (Cutting a Line Segment to Size) to trim this new segment until it is length $b$. Call the result $S_2$.
Now, use Postulate 1 to connect the endpoints of $S_1, S_2$ by a straight line. Together, these three line segments form a triangle, with one right angle at $p$, and side lengths $a,b$ as required.

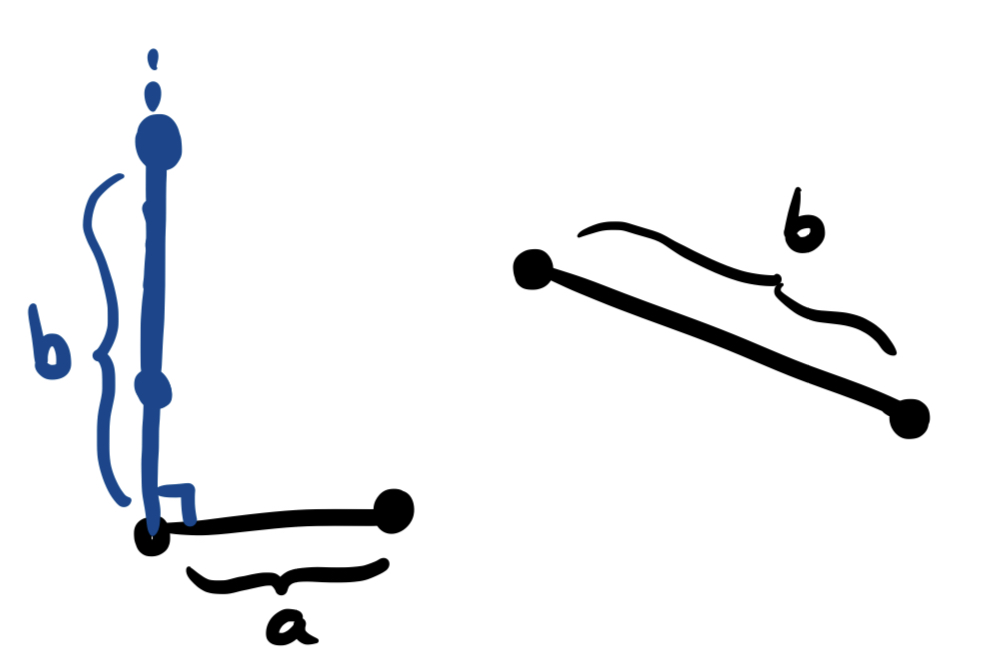
Knowing that right triangles exist, its natural to ask next how we can tell when two right triangles are congruent. But we already have that tool: we can use Euclid’s proposition asserting Side-Angle-Side congruence to conclude right triangles are congruent if and only if their legs are the same length.

We’ve already learned quite a bit about triangles in absolute geometry, though we haven’t quite exhausted the possible knowledge. Euclid goes on to prove a few more propositions, before reaching the final general congruence test for triangles in the 26th:

Proposition 1.7 (Angle-Side-Angle Congruence: Elements Prop 26) Two triangles are congruent if they have two equal pairs of angles, and an equal corresponding side.

Again, we give a quick application of this triangle congruence, and complete the converse of Proposition 1.3.

Proposition 1.8 (Equilateral if Equiangular) Prove that a triangle with three equal angles has three equal sides. This proves that a triangle is equilateral if and only if it is equiangular.

Proof. Let $ABC$ be an equiangular triangle, so the angle measures at $A,B$ and $C$ are all equal.
Choose one of the angles - say $B$ - and bisect it with a line. This line divides the triangle into two smaller triangles, which we see are congruent (they share a side: the new bisecting line, as well as two angles since they each have one of the original angles, and one of the bisected halves). Thus, the remaining pairs of sides of this triangle are also congruent, so $BA$ equals $BC$.

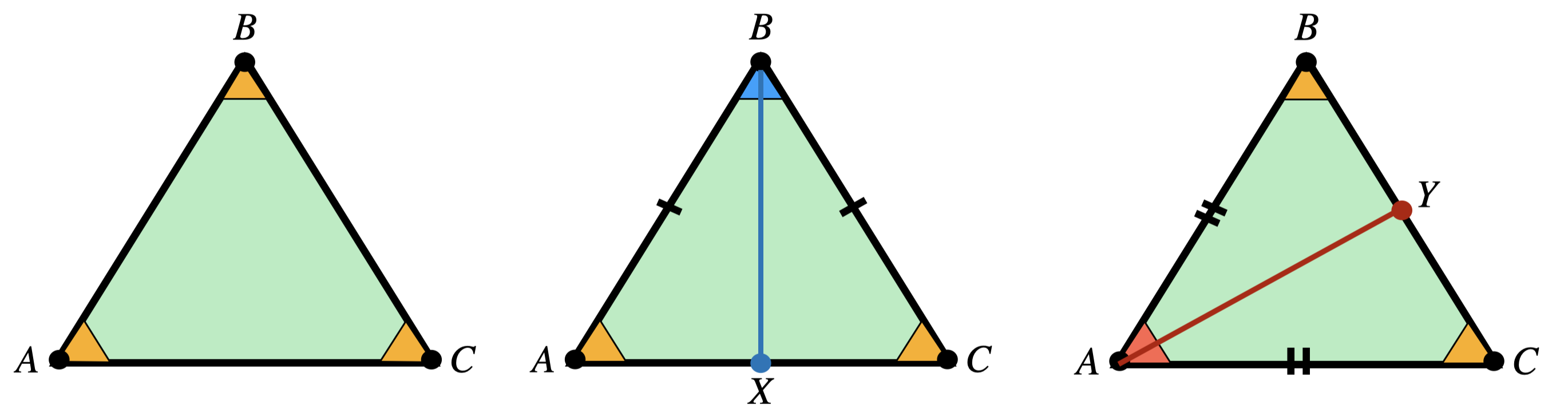
There was nothing special about the angle $B$, so we may also do the same construction at another angle - say $A$. This again gives a pair of congruent triangles, from which we can conclude that $AB$ equals $AC$.

Stringing these equalities together, we see that $AB=AC=BC$ so all three sides are equal, and the triangle is equilateral.

Exercise 1.2 Prove that inside of an equilateral triangle, you can inscribe an upside down equilateral triangle of exactly half the side length, as in the figure below. In your proof, feel free to use any of the Postulates, as well as any proposition stated above this point.