32 Relativity
32.1 Symmetries of Spacetime
We’ve shown there are two possible ways the symmetries of spacetime could behave: it can either follow the laws of the Galilean Group \(G\):
\[G=\left\{\begin{pmatrix} 1& -v \\ 0& 1 \end{pmatrix}\Big | v\in\RR \right\} \]
Or, it can follow the symmetries of the Lorentz Group \(L\) \[L=\left\{\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\begin{pmatrix} 1& -v \\ -v/c^2& 1 \end{pmatrix}\Bigg| v\in(-c,c)\right\} \]
Where these are applied as linear transformations to the spacetime of events \(e=(x,t)\) for \(x\in\RR, t\in\RR\). While the Galilean group has much more intuitive consequences, it turns out the real world exhibits Lorentz symmetry, and we focus on the strange consequences of that here.
32.1.1 Observers in Spacetime
Objects in the world are modeled by curves in spacetime \(\gamma(s)=(x(s),t(s))\). An object is said to be stopped at some instant \(s_0\) if its \(x\) coordinate is not changing: \(x^\prime(s_0)=0\). An object is stopped for a interval if this holds for all points in that interval: equivalently, if \(x\) is constant for \(s\in[a,b]\). An object described by \(\gamma\) is stoppable at \(s_0\) if there is some Lorentz transformation \(L(v)\) where the curve \(L(v)\gamma(s)\) is stopped at \(s_0\): equivalently if \(L(v)\gamma^\prime(s_0)\) is parallel to \(\langle 0,1\rangle\).
In the coordinates \((x,t)\) of an observer \(O\) who is stationary at \(x=0\), we define the speed of an object \(\gamma\) relative to \(O\) to be the change in \(x\) over the change in time. That is, the average speed over an interval \(s,s+h\) is
\[\frac{x(s+h)-x(s)}{t(s+h)-t(s)}\]
Exercise 32.1 Show the instantaneous speed is expressible as a derivative \[v=\frac{x^\prime(s)}{t^\prime(s)}\]
An observer is called constant speed if this \(v\) is constant as a function of \(s\). Such constant speed trajectories describe affine lines in spacetime.
Galileo’s principle says that anyone’s viewpoint on the world is equivalent - that is, that anyone can imagine themselves as not moving. This gives a constraint on the set of curves that describe trajectories we can move on, which we will call observer trajectories. Every observer trajectory must be locally stoppable at each point, in order to obey Galileo’s principle.
In a world with Lorentz symmetry, this already poses a strong constraint: because \(L(v)\) is defined only for \(v\in(-c,c)\) and \(L(v)\) takes the vector \(\langle -v,1\rangle\) to \(\langle 0,1\rangle\), we see that ONLY trajectories with speed less than \(c\) are stoppable, and so observers can only travel at speeds less than the constant \(c\)!
While trajectories moving at speed \(c\) are ruled out for observers, they are not immediately disallowed overall. However such trajectories have some very strange properties:
- An object moving at speed \(c\) can never be stopped: it must always move!
- You cannot run away from an object moving at speed \(c\): no matter your speed, you will always see it approaching you at speed \(c\)!
Thus not only must such objects never stop moving, but they can never even slow down! They must always travel at speed \(c\).
32.2 Measuring Time along a Trajectory
If \(\gamma(s)\) is the trajectory of some observer through spacetime, one may ask between the points \(\gamma(a)\) and \(\gamma(b)\), how much time elapses for that observer. We need to find a way to calculate this quantity. Here’s an alternative argument to the one given in class (this is perhaps more like the ‘physics way’ starting with a simple case and then building up)
If the observer is stationary, this is easy: the vertical axis is defined as the time axis of a stationary observer, so we just measure the difference in \(t\) coordinates. But for any other observer this is not possible. However, this suggests a strategy to calculate the time duration of a constant speed observer: if an observer moves at speed \(v\) can use the Lorentz boost \(L(v)\) to make them stationary, at which point we can read off from the time axis exactly how long of a time they experienced. For example, using homogenity of spacetime to have our constant speed observer pass through the origin, we may write \[\gamma(s)=(vs,s)\] and then \[L(v)\gamma(s)=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\begin{pmatrix} 1& -v \\ -v/c^2& 1 \end{pmatrix}\begin{pmatrix}sv\\s\end{pmatrix}\]
\[\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\begin{pmatrix}sv-sv\\ -sv^2/c^2+s\end{pmatrix} =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\begin{pmatrix}0\\s\left(1-\frac{v^2}{c^2}\right) \end{pmatrix}\]
So, between \(s=a\) and \(s=b\) this observer themselves really experiences the time \[T=(b-a)\sqrt{1-\frac{v^2}{c^2}}\]
On a general curve \(\gamma\) we need to instead take an infinitesimal approach, as at each point the observer may be moving at a different speed \(v=x^\prime/t^\prime\). For an infinitesimal interval around this point, the time \(dT\) which passes is proportional to \(ds= b-a\) by the above formula, and
\[\Delta T=\Delta s \sqrt{1-\frac{v^2}{c^2}}\]
Taking the limit as the interval shrinks to zero and integrating gives the following result for curves of the form \(\gamma(s)=(x(s),s)\) (this constraint is only because we used the curve \((sv,s)\) as our initial starting point!)
\[T=\int \sqrt{1-\frac{v^2}{c^2}}ds=\int \sqrt{1-\frac{x^\prime(s)^2/t^\prime(s)^2}{c^2}}ds\]
32.2.1 Another Way
We could also carry out this calculation more abstractly (this is the ‘math way’ that we did in the independent study): we know that spacetime with Lorentz symmetries preserves the dot \((x^\prime)^2-c^2(t^\prime)^2\) on tangent vectors, from our previous assignments. Looking at this dot product, the units we have written it in are space-units (if \(x\) is in meters and \(c\) is in meters per second, then \(ct\) is also in meters…). But, if we wanted to measure everything in time-units (perhaps more intuitive for us, who are trying to understand durations) we could do that just as easily. Dividing this entire dot product through by the constant \(c^2\) gives
\[\frac{(x^\prime)^2}{c^2}-(t^\prime)^2\]
Which is also preserved (as its just a constant multiple of the original) but now has the same units that \(t\) does (so, if we are thinking of time in seconds, the output of the norm will be seconds). If \(\gamma\) is the trajectory of some observer, then \(\gamma^\prime=(x^\prime,t^\prime)\) is moving at speed \(v=x^\prime/t^\prime\) less than \(c\), and so there is a Lorentz transformation \(L(v)\) bringing it to a stop. This transformation must take its tangent vector to a vector along the vertical \(t\) axis, but also cannot change the length with respect to this preserved inner product! Thus, the duration we would measure for time must simply be the norm \[\|\gamma^\prime\|=\sqrt{\Big|\frac{(x^\prime)^2}{c^2}-(t^\prime)^2\Big|}=\sqrt{(t^\prime)^2-\frac{(x^\prime)^2}{c^2}}=\] \[=t^\prime\sqrt{1-\frac{(x^\prime)^2/(t^\prime)^2}{c^2}}=t^\prime\sqrt{1-\frac{v^2}{c^2}}\]
Integrating this over a curve gives
\[\mathrm{Time}(\gamma)=\int_a^b t^\prime(s)\sqrt{1-\frac{v(s)}{c^2}}ds\]
And, for curves of the form \(\gamma(s)=(x(s),s)\), we see \(t^\prime=1\) and this agrees with our previous formula from the physics derivation. A side note: we can always parameterize a curve like this if we want, so there is no loss of generality here! Because our curve is a negative curve, we know that \(t^\prime\) is always positive, and so \(t\) is an increasing function. Thus, \(t\) has an inverse function and we can use that inverse to reparameterize: the equations \((x(s),t(s))\) and \((x(t^{-1}(s)), t(t^{-1}(s)))\) trace out the same curve in spacetime, but \(t(t^{-1}(s))=s\) so the second is just of the form \((f(s),s)\) for some \(f\).
Now we can proceed from this general statement applicable to all curves, to specialize for constant speed trajectories. Say that \(\gamma\) is a constant speed curve connecting the spacetime events \(p=(x_p,t_p)\) and \(q=(x_q,t_q)\). Then one way to parameterize this affine line is \[\gamma(s)=p+s(q-p)\] where \(\gamma(0)=p\) and \(\gamma(1)=q\). The derivative of this is just \((x^\prime, t^\prime)=q-p=(x_q-x_p,t_q-t_p)\), and so
\[\mathrm{Time}(\gamma)=\int_0^1 \|\gamma^\prime\|ds = \int_0^1 \sqrt{(t^\prime)^2-\frac{(x^\prime)^2}{c^2}}ds=\int_0^1\sqrt{(t_q-t_p)^2-\frac{(x_q-x_p)^2}{c^2}}ds\] \[=\sqrt{(t_q-t_p)^2-\frac{(x_q-x_p)^2}{c^2}}=\sqrt{\Delta t^2-\frac{\Delta x^2}{c^2}}\]
This is a remarkably understandable formula! (Even if the consequences are wild) In a diagram, we are measuring the duration experienced along a trajectory simply by the Minkowski Pythagorean Theorem! Take the difference in time coordinates \(\Delta t\), the difference in space coordinates \(\Delta x/c\) (dividing by \(c\) puts it in units of time) and then apply \(a^2-b^2\)!
Side Note: we can rewrite this in terms of the speed \(v=\Delta x/\Delta t\) so it matches up with the physics derivation, factoring out \(\Delta t\) from the root: \[\mathrm{Time}(\gamma)=\Delta t \sqrt{1-\frac{(\Delta x/\Delta t)^2}{c^2}}=\Delta t\sqrt{1-\frac{v^2}{c^2}}\]
32.3 The Flash vs a Flashlight
Imagine the following setup: you and The Flash are standing still right next to one another, at a distance of \(d\) from your friend who is also standing still relative to you both, and is holding a flashlight. At some point in time, your friend turns on the flashlight, and immediately The Flash takes off, running away from the light beam at speed \(v\).
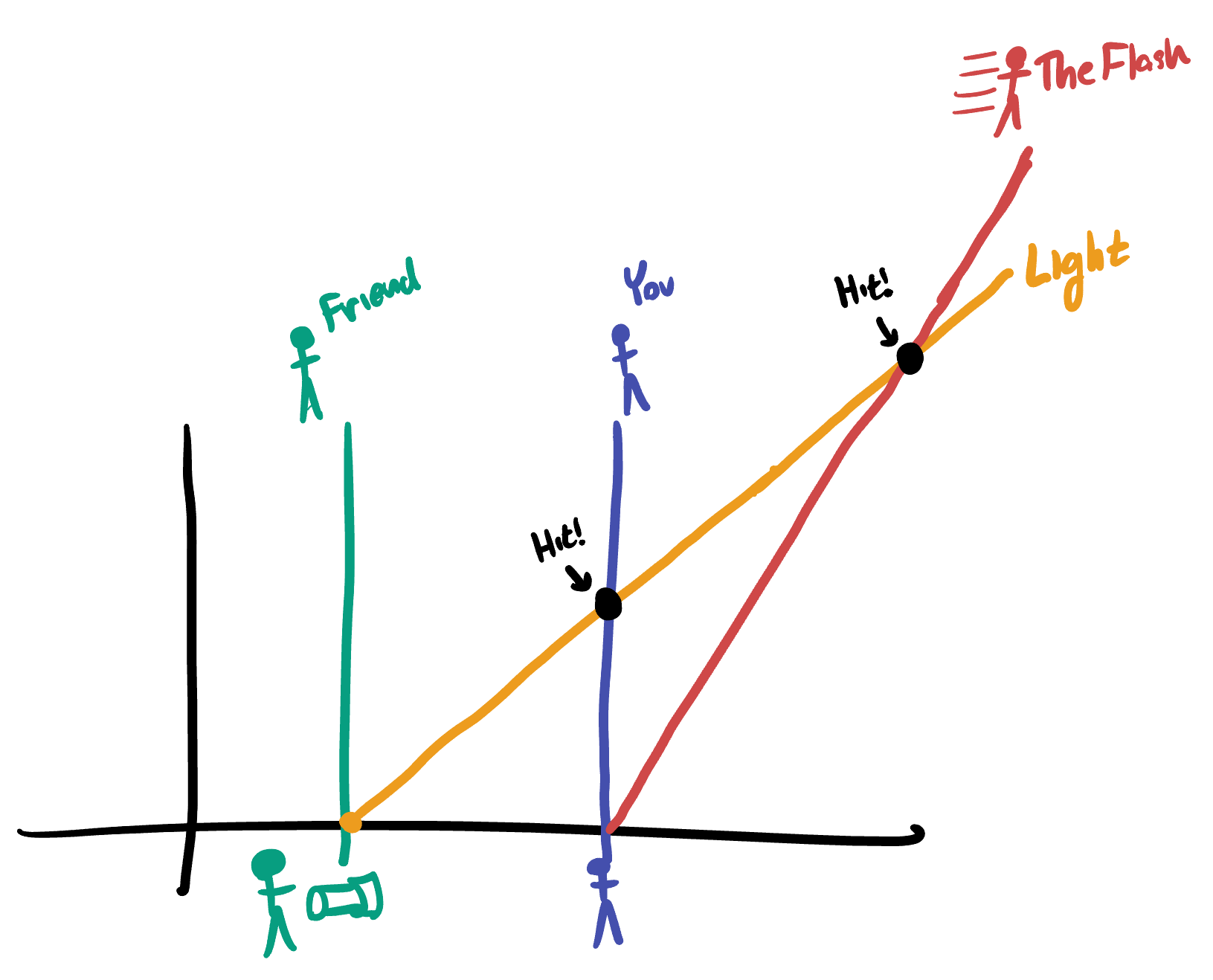
Exercise 32.2
- How much time passed on your clock, by the time the light hits you?
- How much time passes on The Flash’s clock, by the time the light hits him?
- What time will your clock read at the moment that The Flash is hit?
- What time will your clock read when you see The Flash get hit?
32.4 The Twin Paradox
Two twins start out right next to one another. One of decides to stay where they are, and just hang out. The other gets into an fast moving ship and goes on a joyride, following some trajectory \(\gamma(s)\) through spacetime, but eventually coming back to where they started.
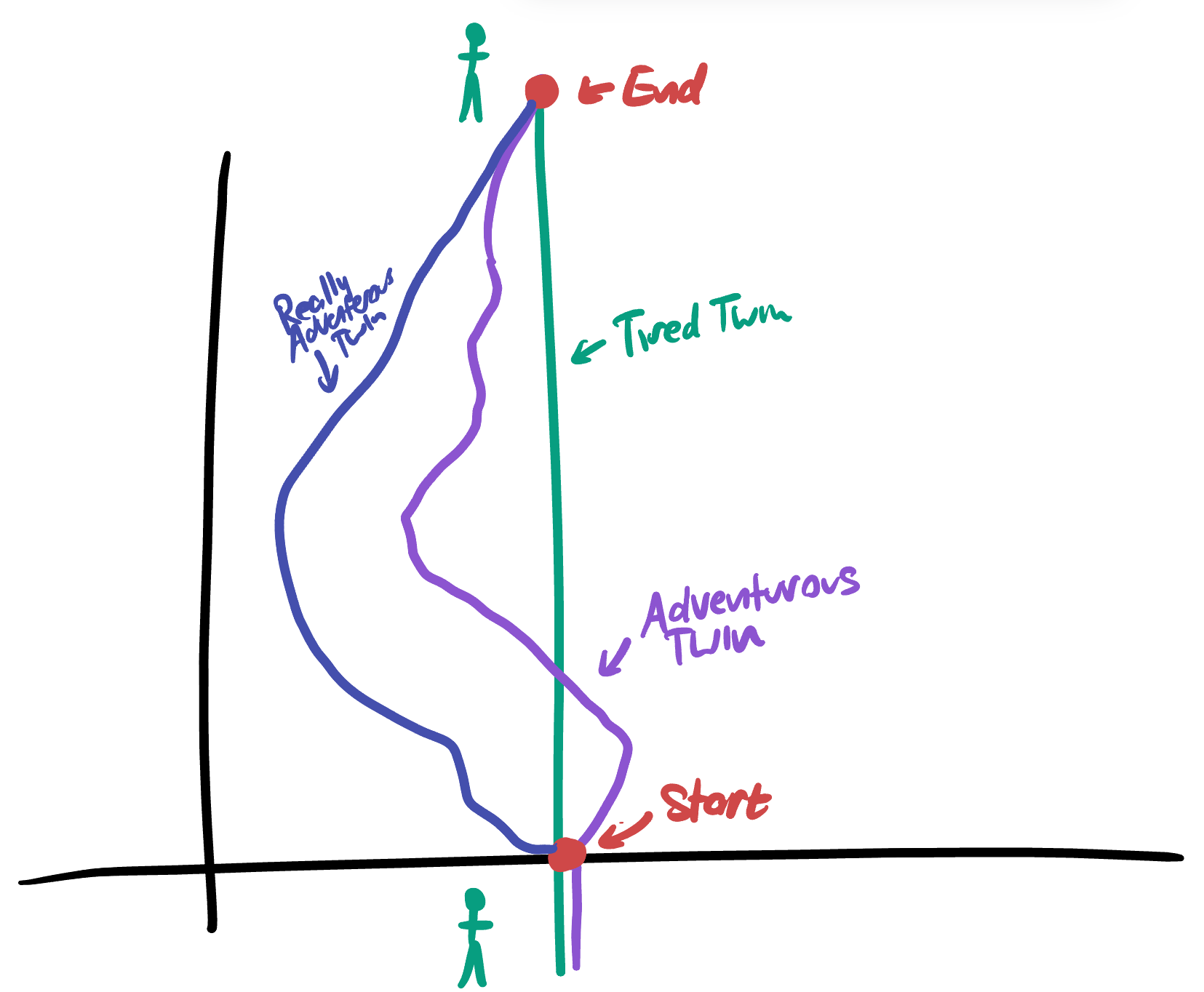
Exercise 32.3 Prove that no matter what trajectory \(\gamma\) the adventurous twin travels on, so long as they leave home they return younger than the twin who stayed at home.
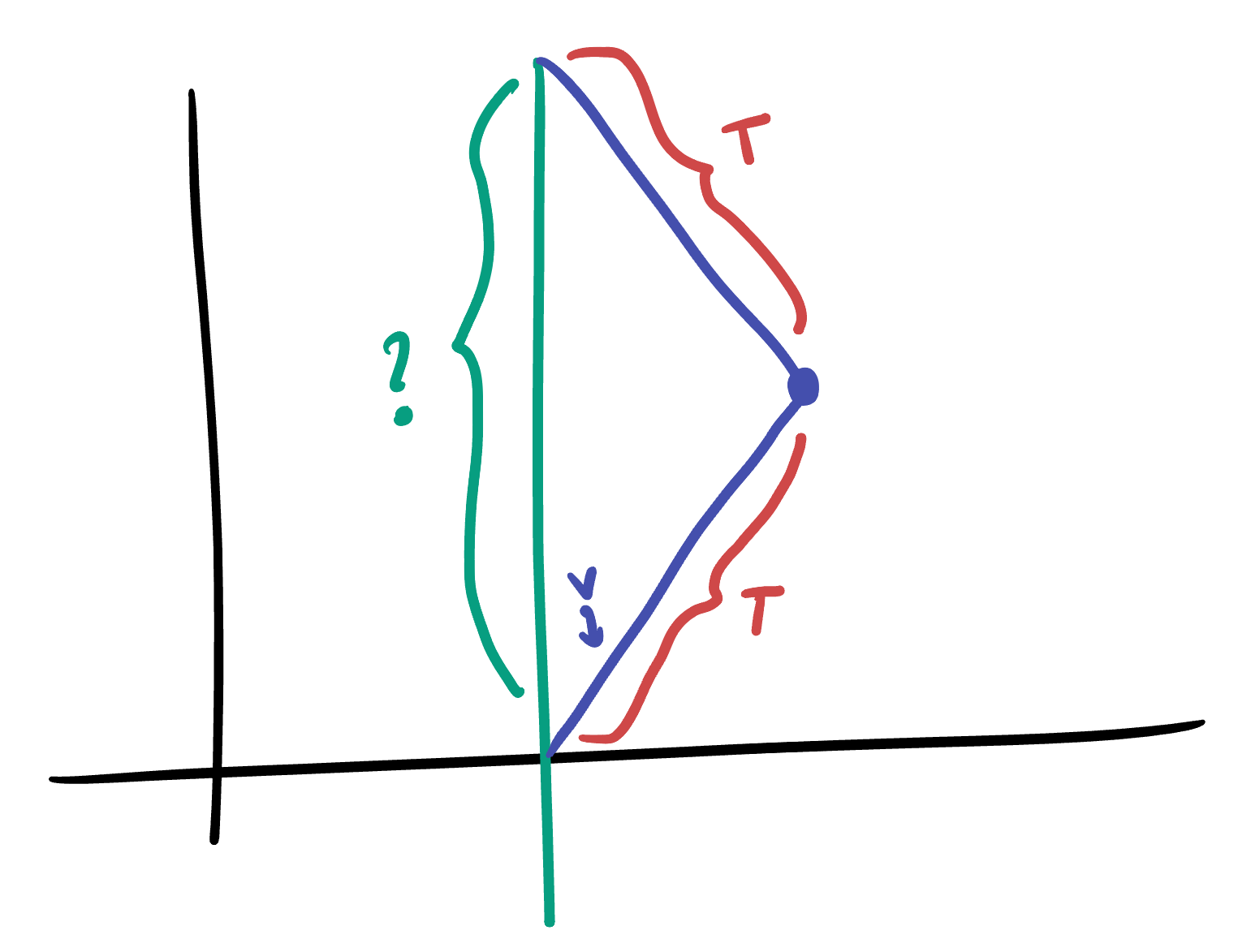
Exercise 32.4 Say that the adventurous twin leaves home at velocity \(v\), and travels for \(T\) units of time (on his clock), and then turns around and heads home by the same manner (traveling at velocity \(v\) for time \(T\)). How old is his twin when he gets back?
32.5 Neither Before nor After
In the Galilean world, everyone agrees which slices of spacetime counts as “space”. These slices define a universal notion of time: given any two events \(p=(x_p,t_p)\) and \(q=(x_q,t_q)\), the time difference \(t_p-t_q\) is a number that any Galilean observer could compute from \(p\) and \(q\) and would agree on. We’ve seen already that things are much stranger in the Lorentzian world, where the time difference between events (like two twins departing, and then reuniting again) differs wildly depending on who you ask.
But, surely the order events occur in is invariant across observers, even if the precise length of time elapsed between them is not - right? Right??
Exercise 32.5 (Wrong) Consider an observer \(O\) who is not moving with respect to \((x,t)\), and imagine two events in spacetime \(p\) and \(q\) that he agrees occur at the same time. Show that there is also an observer who claims that \(p\) happens before \(q\), and an observer who claims that \(p\) happens after \(q\).
Hint: If \(p\) and \(q\) occur at the same time for \(O\) then they have the same \(t\) coordinate. Apply a Lorentz boost \(L(v)\) and compare the resulting \(t\) coordinates. What about \(L(-v)\)?
But not all is lost: there are still pairs of events where everyone agrees the order they occurred in: for instance, it is a fact of the matter that I lived in Minnesota before I lived in California, and not the other way around. Everyone, even fast traveling aliens watching us through super telescopes agrees with this.
:::{#rel-prob-5} Show that if \(p\) and \(q\) are two events on the trajectory of some observer, and \(p\) happened before \(q\) for that observer, then everyone agrees that \(p\) happened before \(q\). :::
Hint: Show if \(\gamma\) is the trajectory of some observer with \(\gamma(a)=p\) and \(\gamma(b)=q\) then \(\|q-p\|^2\) is negative. And, because spacetime is homogeneous, you might as well consider \(p=(0,0)\) is the origin. Then show that if \(q=(x,t)\) is a point with \(t>0\) and \(\|q-p\|=\|q-0\|^2=\|q\|^2\) negative, then every Lorentz transformation applied to \(q\) leaves its time coordinate positive, so it always occurs after \(p\), whose time coordinate is zero.
Thus spacetime has events where it is undefined which came first, and others where it is unambiguous which was first. And, there are no events which unambiguously occur at the same time! (This is what physicists call the “Relativity of Simultaneity”). In fact these two types of pairs of events have a nice math interpretation: the ones which can be ordered in time are the pairs of points with negative separation (from our linear algebra chapter) and those which cannot are those with positive separation.
If you feel like getting really confused, this is a good time to go back and think about The Flash and the Flashlight: remember we said that from our friend with the flashlight’s perspective, the following events are simultaneous:
- Him turning on the flashlight
- You and the Flash being right next to one another.
Since you are not moving relative to your friend, you both agree that these events are simultaneous. But The Flash does not! In fact, from the Flash’s perspective, the flashlight is not turned on until much later than he started running: this means from his perspective, there is much more distance for the light to cover before overtaking him (as he had a head start).
Exercise 32.6 Draw in space slices for The Flash into the diagram, and see that the space slice through the point where the flash runs away from you intersects your friend far before he turned on the flashlight. Use geometry and Lorentz transformations to figure out how long after the flash starts running he thinks the flashlight is turned on.
32.6 You Can’t Go Back
The grandfather paradox is a classic time travel story that highlights one of the absurd consequences of entertaining time travel into the past. In it, starting from wherever you are right now, you travel along some path in spacetime and eventually you end up back inside the past light cone of your starting point: somewhere where actions you undertake could affect you where you started!
The classical example is rather violent: you arrive at a time before your parents were born, and kill one of your grandfathers. Thus, no parents, and no you. But how could this be possible, since you exist - after all its you who went back and did this! The one can be much less violent and arrive at similar absurdities: what if along your journey you bring your favorite book to read; and upon your arrival in your past, you meet the author before he has written it. You give him a copy, remarking how much you loved it. If he then reads it, agrees, and submits it for publication, who wrote the book?
In fact, this book example provides a much better picture of what must be going on mathematically than the grandfather case. Indeed, track the book: starting in your hand, it follows you (on an observer’s trajectory) until it meets the author, at which point it changes hands and follows the author (also an observer’s trajectory) until it ends up on a bookstore’s shelf, and then gets into your hands! At each point in time the book was following an observer’s trajectory (either literally with you or the author, or sitting motionless on a shelf), but at the end of its journey it ended up at the same spacetime event where it began.
That means the trajectory of our book is a closed curve: a loop in spacetime!
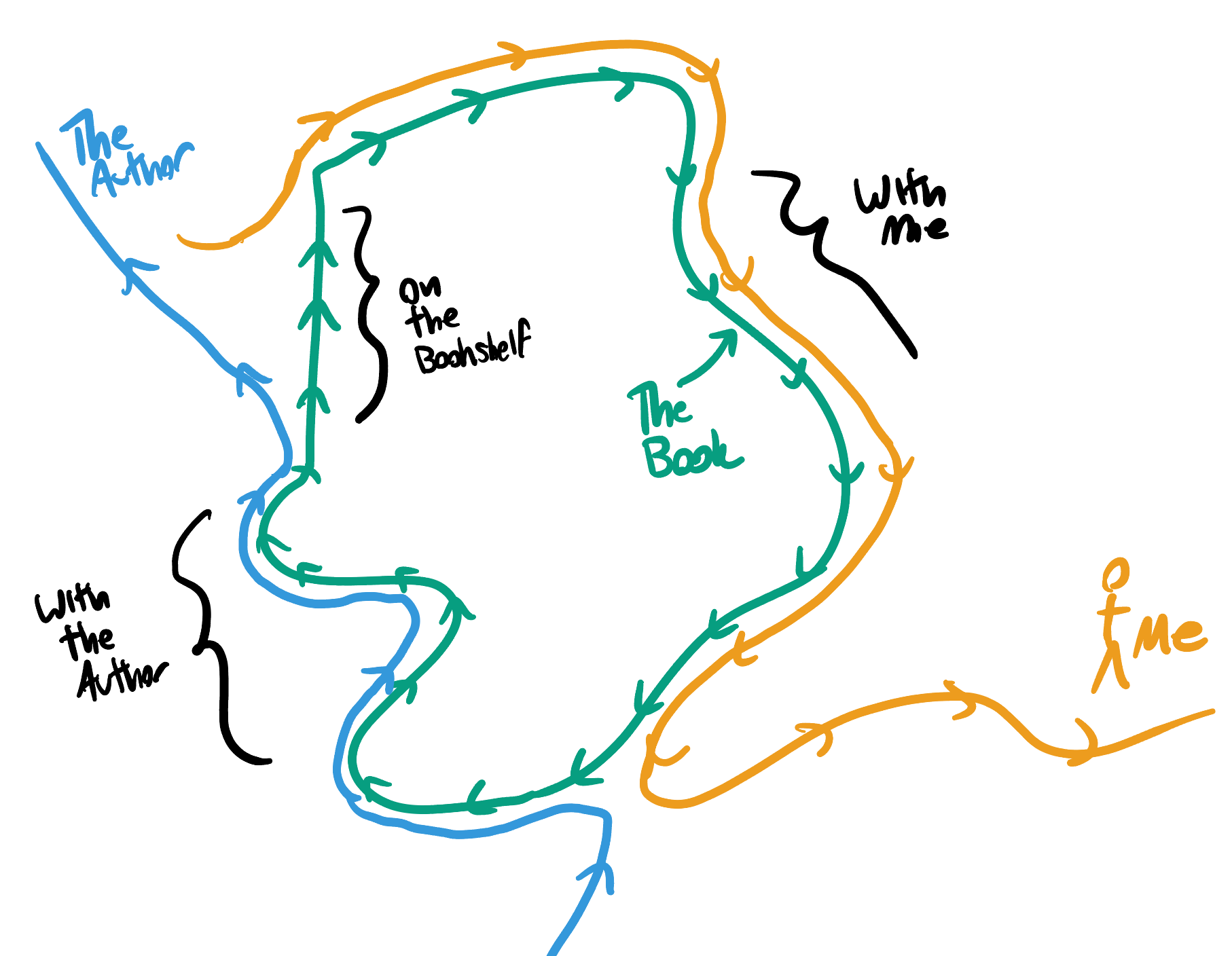
Exercise 32.7 Show that there are no closed observer trajectories in spacetime with Lorentzian symmetries. Thus, you can never visit the past!
Hint: An observer trajectory must always have its tangent vector lying inside the negative cone. But if \(\gamma(s)=(x(s),t(s))\) were a closed curve, then use some real analysis to show that the \(t\) component must have a point where \(t^\prime(s_0)=0\). But this is a problem!! Why?