$$$$

29  A Strange Inner Product

In the rest of this book, we bring our tools of geometry to study an space that shares many similarities with Euclidean geometry, but one major difference right at the beginning: the dot product that we use to measure infinitesimal distances and angles has a minus sign in one place it used to have a plus.

Definition 29.1 (Minkowski Inner Product) We write ${\mathbb{R}}^{2,1}$ to mean a 3-dimensional real vector space together with the inner product $$⟨a,b,c⟩\star ⟨x,y,z⟩=ax+by-cz$$ Its often useful to write this in matrix form, where $J$ is the diagonal matrix $J=\mathrm{diag}(1,1,-1)$:

$$v\star w=v^{T}Jw$$

The level sets of the Euclidean inner product are circles. The level sets of the Minkowski inner product are hyperbolas, together with a union of two lines as the degenerate level set $x^2-z^2=0$.

More generally, we write ${\mathbb{R}}^{n,m}$ for the $n+m$ dimensional real vector space whose inner product is of the above form, with $n$ pluses and $m$ minuses, and as shorthand write ${\mathbb{R}}^n$ for ${\mathbb{R}}^{n,0}$ (the standard inner product, where all signs are $+$)

Definition 29.2 Minkowski space is the 3-dimensional geometry where every tangent space is a copy of ${\mathbb{R}}^{2,1}$ (just like Euclidean space has the standard inner product on the tangent space at every point).

Our primary goal is to practice using the techniques we have developed in geometry in a new an unfamiliar setting, but this particular space was chosen for a reason: there will be some exciting payoffs along the way.

This is the geometry of special relativity, but our first introduction to it actually comes through its intimate relationship to hyperbolic geometry. We will see that just like the sphere ${\mathbb{S}}^2$ naturally lives inside of Euclidean 3-space (as the level set of the dot product $v\cdot v=1$), hyperbolic geometry ${\mathbb{H}}^2$ naturally lives inside of Minkowski space (as part of the level set of the dot product $v\star v=-1$).

$$\{(x,y,z)\in {\mathbb{R}}^{2,1}\mid x^2+y^2-z^2=-1\}$$

The level sets of the Minkowski inner product in ${\mathbb{R}}^{2,1}$, and the $-1$ level set: a hyperoloid of two sheets.

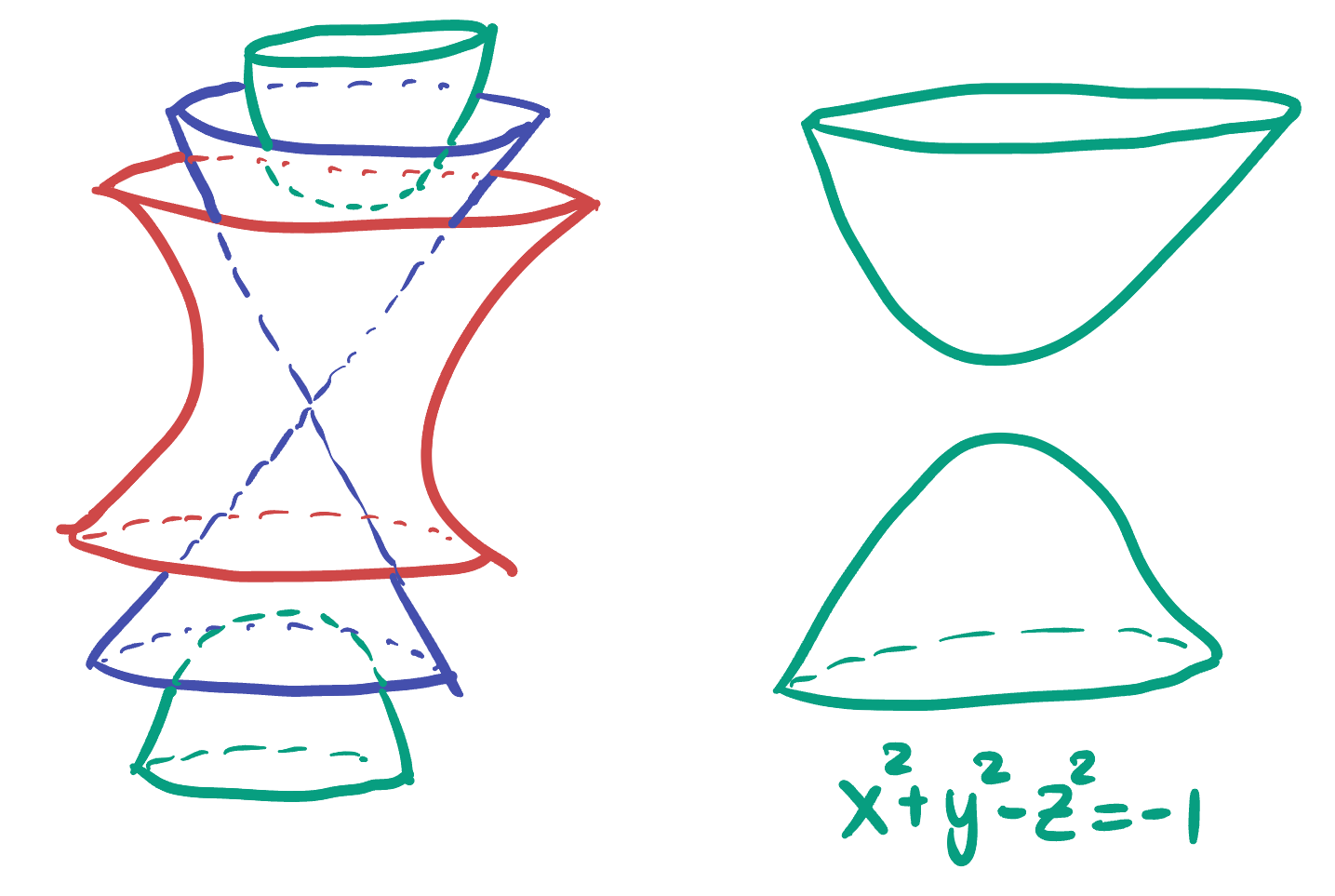
29.1 Isometries of Minkowski Space

As a first step to understanding this, we aim to take as much of our understanding of ${\mathbb{S}}^2$ inside of ${\mathbb{R}}^3$ as we can and build analogies to the hyperboloid in Minkowski space. In Euclidean geometry, we found the isometries of the sphere inside of the isometries of Euclidean space, as precisely the isometries which fix the origin (all others were translations). So here we will attempt to classify the isometries of Minkowski space, and inside of this, find those that preserve the hyperboloid.

Definition 29.3 Recall that if $X$ is any geometry (where we write $⟨-,⟩$ for its inner product on each tangent space), an isometry is a map that preserves this inner product, a $\varphi :X\to X$ where at each point $p$, and for every $v,w\in T_{p}X$ we have

$$⟨v,w⟩=⟨D{\varphi }_p(v),D{\varphi }_p(w)⟩$$

The same is true for Minkowski space, where a Minkowski isometry is any map $\varphi :{\mathbb{R}}^{2,1}\to {\mathbb{R}}^{2,1}$ such that

$$v\star w=D{\varphi }_p(v)\star D{\varphi }_p(w)$$

Theorem 29.1 Translations $T(x,y,z)=(x+a,y+b,c+z)$ are isometries of Minkowski space.

Exercise 29.1 Prove this via a computation

Since a translation can take any point to any other point, we see already that Minkowski space is homogeneous. Thus, the only remaining isometries to consider are those that fix the origin (every isometry can be built as a composition of one that fixes the origin, and a translation). Studying these generally sounds difficult, so we start by studying linear isometries: recall an isometry $\varphi$ is linear if it is given by matrix multiplication: $\varphi (p)=Ap$ for some $3\times 3$ matrix $A$, for every point $p=(x,y,z)$.

Theorem 29.2 Show that a linear map $\varphi (p)=Ap$ is a Minkowski isometry if and only if $A^{T}JA=J$ for $J=\mathrm{diag}(1,1,-1)$.

This reduces the classification of linear isometries to understanding solutions of a matrix equation. We can understand such solutions in analogy with the more familiar equation $A^{T}A=I$ specifying linear isometries of ${\mathbb{R}}^3$

Theorem 29.3 Show that solutions of the equation $A^{T}JA=J$ are matrices $$A=\left(\begin{array}{ccc}|& |& |\\ a_1& a_2& a_3\\ |& |& |\end{array}\right)$$ Where $a_i$ and $a_j$ are Minkowski-orthogonal if $i\ne j$, and each column is of Minkowski norm $\pm 1$ (precisely, $a_1\star a_1=a_2\star a_2=1$ but $a_3\star a_3=-1$)

Its easy to find some such matrices, using things we already know about Euclidean geometry.

Theorem 29.4 Show that any Euclidean rotation of the $x,y$ plane that fixes the $z$ axis is a Minkowski isometry. Show that reflecting in the $xy$ plane, so $R(x,y,z)=(x,y,-z)$ is also a Minkowski isometry.

Thus, we can understand isometries that rotate the hyperboloid or exchange the two sheets easily, as they are just the Euclidean isometries we are used to! But there are more isometries of Minkowski space than just this: thinking back to the sphere in ${\mathbb{R}}^3$, we have essentially just found the “rotations about the $z$ axis” so far, and a reflection. What are the analogs of rotations about the other axes?

Since we understand rotations in the $xy$ plane just fine, we can restrict ourselves to isometries which do no such rotation: for specificity, we can focus on isometries for the moment which fix the $x$ axis. This let’s us drop the dimension of our problem by one, and think about just the slice $x=0$, or the $yz$ plane.

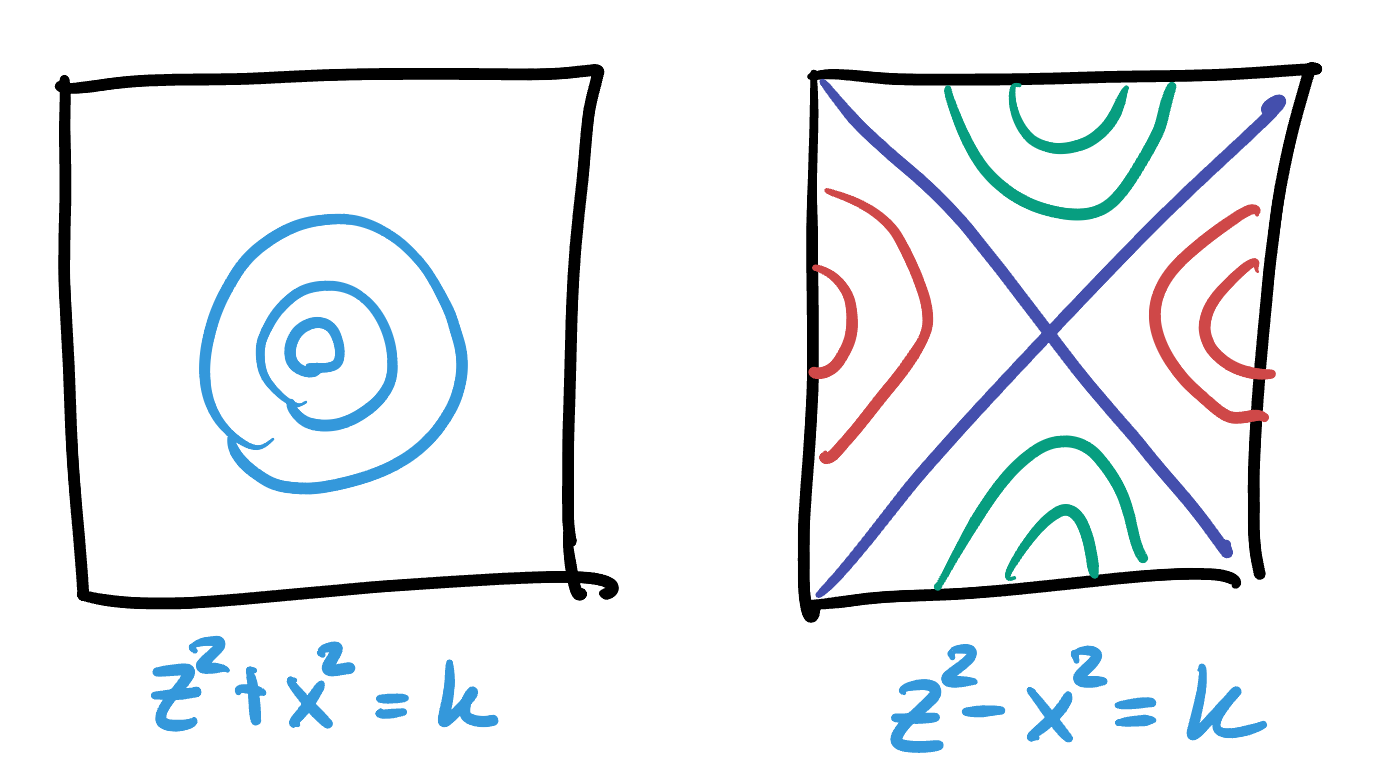
29.2 Isometries of ${\mathbb{R}}^{1,1}$

On this slice of the hyperboloid, our inner product has went from $⟨a,b,c⟩\star ⟨x,y,z⟩=ax+by-cz$ to just $$⟨b,c⟩\star ⟨y,z⟩=by-cz$$

This is a 2-dimensional plane with one $+$ and one $-$, so is a copy of ${\mathbb{R}}^{1,1}$. This is an incredibly useful space because it incorporates all the strange behavior of Minkowski space in a nice 2 dimensional picture we can see. Here, we imagine this space as what we get from looking at Minkowski 3-space with the $x$ axis pointed directly at us: isometries of ${\mathbb{R}}^{1,1}$ correspond to isometries fixing the $x$-axis, which in turn we can think of as the Minkowski analog of ‘rotations about the x axis’ in ${\mathbb{R}}^3$.

Theorem 29.5 Show that the Linear isometries of ${\mathbb{R}}^{1,1}$ are given by matrices of the form $$\left(\begin{array}{cc}a& b\\ b& a\end{array}\right),a^2-b^2=1$$ As well as these followed by a reflection in the $z$ axis, $(y,z)\mapsto (y,-z)$ (which then switches the upper hyperboloid and the lower one) Hint: Find the Minkowski-Orthonormal Bases of ${\mathbb{R}}^{1,1}$!

The matrices given above are exactly the linear isometries of ${\mathbb{R}}^{1,1}$ which preserve the upper hyperbola, and so correspond to isometries of Minkowski space that preserve the upper hyperboloid and fix the $x$ axis! Like in Euclidean space, we can parameterize these isometries using trigonometric functions: there we used that $a^2+b^2=1$ is satisfied by $a=\cos t,b=\sin t$, and here we use $a^2-b^2=1$ is the defining trigonometric relation for $a=\cosh t$ and $b=\sinh t$

Corollary 29.1 The linear isometries preserving the upper hyperboloid of ${\mathbb{R}}^{1,1}$ are all of the form $$\varphi (y,z)=\left(\begin{array}{cc}\cosh t& \sinh t\\ \sinh t& \cosh t\end{array}\right)\left(\begin{array}{c}y\\ z\end{array}\right)$$

Its really instructive (and confusing) to use these matrices to try and understand the geometry of ${\mathbb{R}}^{1,1}$. Starting with the vectors $e_1=⟨1,0⟩$ and $e_2=⟨0,1⟩$, we can easily check these are Minkowski orthogonal ($e_1\star e_2=0$): thus if $\varphi$ is any linear isometry we know $D\varphi (e_1)$ and $D\varphi (e_2)$ will also be Minkowski-orthogonal.

Exercise 29.2 Choose some isometries (just pick some value of $t$ and plug it into the matrices above and get decimal approximations, to make it easy to work with) and use them to get a collection of different Minkowski-orthonormal bases in the plane. Draw them! What do they look like? When $t$ gets large, what is happening to the vectors?

Various pairs of Minkowski-orthonormal vectors (each pair is grouped by the blue arrows). Thus our coordinate description of Minkowski space can be very misleading: each vector in this diagram is length $1$, and within each pair the green and red vector are orthogonal!

29.3 Distances in Minkowski Space

Like in any of the geometries we’ve previously visited, computing the lengths of various curves in Minkowski space will teach us a lot about it, and eventually will help us track down the geodesics. There is one small difficulty in generalizing what we already know however - it’s that our inner product can now spit out negative numbers, so our definition of infinitesimal length is not well defined, as it had a square root in it. This is an easy fix: just introduce an absolute value! If $v\in {\mathbb{R}}^{n,1}$ is a tangent vector, we define its Minkowski infinitesimal length as

$$\parallel v\parallel =\sqrt{|v\star v|}$$

Given a definition of infinitesimal length, we can define the length of curves exactly as in Geometry class: if $\gamma :I\to {\mathbb{R}}^{n,1}$ is a curve its derivative ${\gamma }^{\prime }(t)$ gives a tangent vector based at $\gamma (t)$ for each $t$, and the infinitesimal length $\parallel {\gamma }^{\prime }\parallel$ represents an infinitesimal segment of arc. Thus, the lenght of $\gamma$ is recovered via integration:

$$\mathrm{Length}(\gamma )={\int }_I\parallel {\gamma }^{\prime }(t)\parallel dt$$ Where $I=[a,b]$ is the domain of $\gamma$.

Happily, since the inner product is so close to the Euclidean inner product, many simple lengths are easy to compute. The first three exercises below show this by having you find the lengths of several straight lines in the Minkowski plane. But beware - easy to compute does not mean easy to understand!

Example 29.1 In ${\mathbb{R}}^{1,1}$ that the length of a segment of the $y$ axis the same as its Euclidean length: that is, if $\gamma (t)$ parameterizes the $y$-axis from $y=a$ to $y=b$, then $\mathrm{Length}(\gamma )=b-a$.

Example 29.2 In ${\mathbb{R}}^{1,1}$ that the length of a segment of the $z$ axis the same as its Euclidean length: that is, if $\gamma (t)$ parameterizes the $z$-axis from $z=a$ to $z=b$, then $\mathrm{Length}(\gamma )=b-a$.

Example 29.3 In ${\mathbb{R}}^{1,1}$ show the length of any segment of one of the diagonals $y=\pm z$ is ZERO! Thus, Minkowski space has the extremely strange property that curves connecting two distinct points are allowed to have zero length!

In the final exercise here of ‘simple-to-compute-lengths’ we will look at measuring the length of the hyperboloid $y^2-z^2=-1$ in ${\mathbb{R}}^{1,1}$: amazingly, due to the strange dot product we are using, this length also turns out to be easy to compute!

Example 29.4 In ${\mathbb{R}}^{1,1}$, we can parameterize the upper sheet of the hyperbola $y^2-z^2=-1$ by $(y,z)=(\sinh t,\cosh t)$. Show that the Minkowski length of this hyperbola between $(0,1)$ and $(\sinh T,\cosh T)$ is exactly $T$.

The arclength along a hyperbola in Minkowski space.

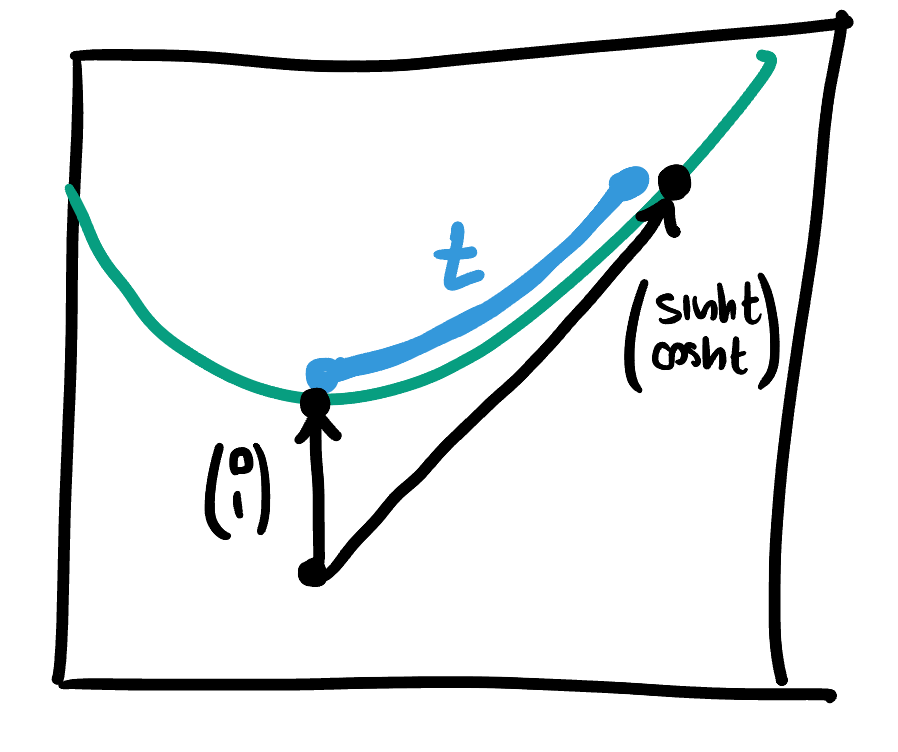
The length of segments of hyperbolas is a useful thing to compute in hyperbolic geometry - as these are the geodesics! The fact that this computation comes out so cleanly in the hyperboloid model is one reason this model is good for computation: in fact in almost all computer programs I write using hyperbolic geometry, I do all the computations in the hyperboloid model because of this.

29.4 Proving the Hyperboloid is Hyperbolic Space

We have learned enough about Minkowski space through its isometries and distances to embark on our main goal: proving that the hyperboloid really is a copy of hyperbolic space! Below is an approach to showing they are the same space, without constructing an isomorphism directly, which we will do so in a series of steps.

Proposition 29.1 STEP 0: The Hyperboloid is Preserved by Linear Minkowski Isometries

Proof. All linear isometries of Minkowski space preserve the inner product $x^2+y^2-z^2$, and so they preserve the Minkowski norm of vectors. That is, if $\varphi$ is any isometry and $p$ is a point of Minkowski space with $\parallel p\parallel =c$ then $\parallel \varphi (p)\parallel =c$ as well. Since the hyperboloid is the level set $\parallel p\parallel =-1$, any Minkowski isometry takes the hyperboloid to itself.

Proposition 29.2 STEP I: The Hyperboloid is Homogeneous For any two points $p,q$ on the hyperboloid $x^2+y^2-z^2=-1$, there is an isometry of the hyperboloid taking $p$ to $q$.

Proof. Like in previous cases, its enough to show your favorite special point can be taken to any other point, if $o\to p$ and $o\to q$ we can compose one with the inverse of the other to send $p\to q$.

Here, a natural special base point for the hyperboloid is $(0,0,1)$. If $p=(x,y,z)$ is any other point on the hyperboloid we may use a Euclidean rotation in the $x,y$ direction to rotate $p$ into the $xz$ plane (such Euclidean rotations are Minkowski isometries, as they preserve the Minkowski inner product - it agrees with the Euclidean inner product on the $xy$ directions!) Thus, without loss of generality we may take $p=(x,0,z)$.

But now, ignoring the $y$ coordinate, we have a point of ${\mathbb{R}}^{1,1}$, which lies on the hyperboloid $x^2-z^2=-1$. We can parameterize this hyperboloid by $(\sinh t,\cosh t)$, so for some particular $t_0\in \mathbb{R}$ we may write $(x,z)=(\sinh (t_0),\cosh (t_0))$. But, by our classification of isometries, we know that the matrix $$\left(\begin{array}{cc}\cosh (t_0)& \sinh (t_0)\\ \sinh (t_0)& \cosh (t_0)\end{array}\right)$$

Is an isometry, and this takes $(0,1)$ to $(\sinh t_0,\cosh t_0)$. Thus, combining this wtih our rotation, we can take $(0,0,1)$ to $p$, and thus $p$ to $q$.

Proposition 29.3 STEP II: The Hyperboloid is Constant Curvature Isometries preserve curvature, so whatever geometry this is, the curvature is the same at every point. Since its constant curvature, its either the sphere the Euclidean plane or hyperbolic space.

Circles on the hyperboloid of Minkowski radius $r$ have circumference $2\pi \sinh (r)$.

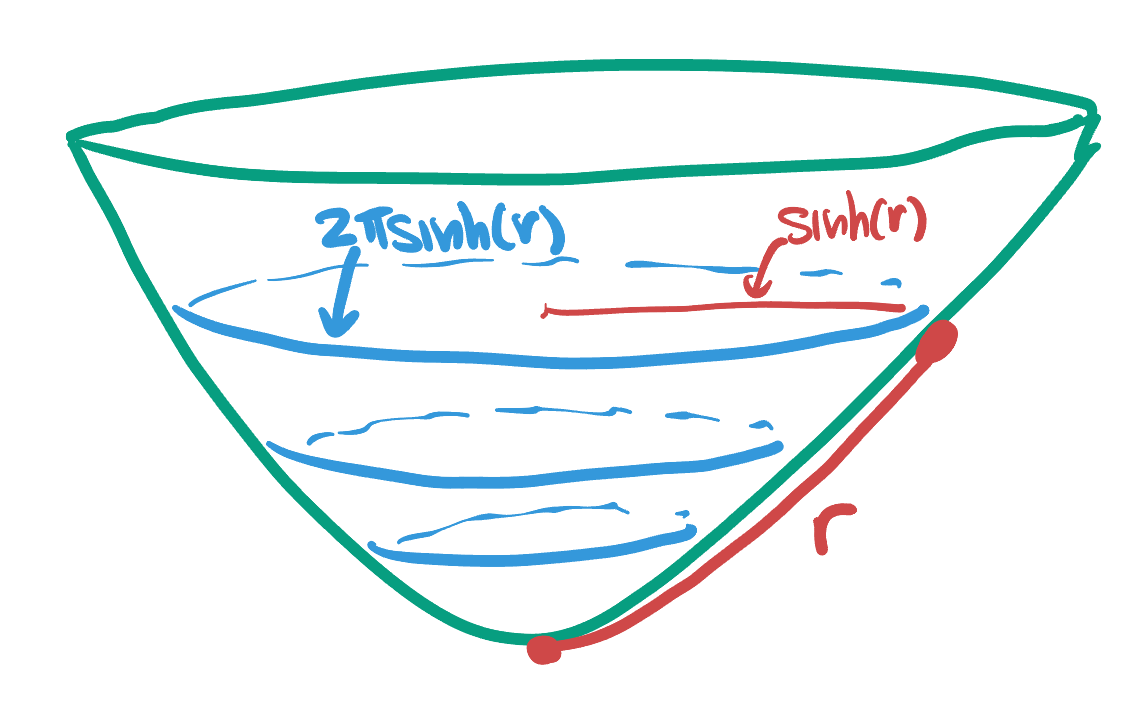
Proposition 29.4 (STEP III: The Curvature is Constant $-1$)  

Proof. To compute curvature, we need to find the formula of circumference of a circle in terms of radius $C(R)$, and compute the limit $$\kappa =\frac{-1}{2\pi }{C}^{\prime \prime \prime }(0)$$

We can find circles of the hyperboloid using isometries: we know that rotations in the $xy$ plane are Minkowski isometries that fix $(0,0,1)$, so if $p=(x,y,z)$ is any point of the hyperboloid and $R$ is any rotation about the $z$-axis, $$\mathrm{dist}(O,p)=\mathrm{dist}(R(0),R(p))=\mathrm{dist}(O,R(p))$$

Thus, $p$ and $R(p)$ lie on the same circle about $O$! Thus, taking an arbitrary point $(x,0,z)$ on the hyperboloid, we find that the circle containing this point is

$$\left(\begin{array}{ccc}\cos t& -\sin t& 0\\ \sin t& \cos t& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ 0\\ z\end{array}\right)=\left(\begin{array}{c}x\cos t\\ x\sin t\\ z\end{array}\right)$$

So we know the circles about $O$ of the hyperboloid, but we don’t know what the radii are: for that, we need to find a geodesic. Recall that geodesics can be found as the lines of symmetry - curves that are fixed by isometries. And, one isometry of Minkowski space is $(x,y,z)\mapsto (x,-y,z)$ This fixes the set $y=0$, so the hyperbola containing $(x,0,z)$ is in fact a geodesic!

For any such $(x,0,z)$ we know that since $x^2-z^{-}1$, we can find some $R$ such that $x=\sinh R$ and $z=\cosh R$. And, from our previous calculation, we know that the length between $O$ and $(\sinh R,\cosh R)$ is just $R$! Thus, the circle parameterized by

$$\gamma (t)=\left(\begin{array}{c}\sinh R\cos t\\ \sinh R\sin t\\ \cosh R\end{array}\right)$$

has a radius of $R$, and all we need to compute is its circumference. This is done via an integral of $\parallel {\gamma }^{\prime }\parallel$, which is just $\sinh R$: thus

$$\mathrm{Length}={\int }_0^{2\pi }\sinh Rdt=2\pi \sinh R$$

So $C(r)=2\pi \sinh r$ and $\kappa =-1$: this is hyperbolic space!

How to tell? Compute some quantity we know in these geometries: say the circumference to radius of circles. Start around (0,0,1): we found the segment of length R ends at (0,sinh R, cosh R). Thus, a circle is a horizontal circle of (Euclidean) radius sinh R. Easy to find arclength in Minkowski space is $2\pi \sinh R$. Thus its hyperbolic space!

29.4.1 Calculating Distance in the Hyperboloid

Distance between $p$ and $q$ is the length of a geodesic. If $p,q$ are arbitrary points then use an isometry to move one to the basepoint $(0,0,1)$. Now need to measure just distance from this to some $p$.

Geodesics in hyperbolic space are equivalently (1) distance minimizing (2) straightest curves (3) lines of symmetry. Easy to find lines of symmetry of the hyperboloid: a reflection in a vertical plane is an isometry, so the geodesic from $(0,0,1)$ to $p$ is just such a segment of a hyperbola. Without loss of generality we can actually rotate things so $p$ lies in the $(x,z)$ plane, and is $(\sinh a,\cosh a)$ for some $a$. But we know from before the length of this segment is just $a$! Thus this is the distance.

How can we write this in a geometrically meaningful way? Note that

$$(0,0,1)\star (\sinh a,0,\cosh a)=-\cosh a$$

And so we can express the distance between points $X=(0,0,1)$ and $Y=(\sinh a,0,\cosh a)$ as $$d=\mathrm{acosh}|X\star Y|$$

Now that we have expressed things in terms of the Minkowski dot product, we can learn alot! The transformations we used to take our general pair of points $p,q$ to $X$ and $Y$ were all Minkowski isometries, and so they preserved distances on the hyperboloid as well as the inner product! That means $X\star Y=p\star q$, and

$$\mathrm{dist}(p,q)=\mathrm{acosh}|p\star q|$$

We can compute distances in the hyperboloid model by just using dot products! This makes something as complicated as computations in curved space reducible to linear algebra! This makes it very helpful to employ the hyperboloid model in computations done on a computer.