4 Archimedes
In all six books and 465 propositions of The Elements, Euclid never attempts to measure the length of a single curve, nor the area of a non-polygonal figure. Pristine, Greek, axiomatic geometry was about lines, and figures made out of them.
Curves were a different sort of object, a different category or type of thing in the mind of some of the ancients. Much as we would never try to measure the length of a gallon, they would never try to measure the length of a curve.
But to Archimedes, it was not a matter of kind, but of technology. Curves could be measured, if only the correct tools for the job could be developed.
4.1 Measurement of the Circle
In 250BCE Archimedes wrote a mathematical text entitled Κύκλου μέτρησις, or “Measurement of the Circle”. While likely much of the text has been lost to time, an important theorem remains
Theorem 4.1 (Area of the Circle: Archimedes) The area of any circle is equal to the area of a right triangle with one side equal to the circle’s radius, and the other side to the circle’s circumference.

This is the first time in greek mathematics that a curved object has been equated to a straight one. The idea of archimedes’ argument is both beautiful and ingenious, but the difficulties of following it through using the mathematics of the time were considerable.
Archimedes began by approximating the circle by a polygon with a large number of sides.
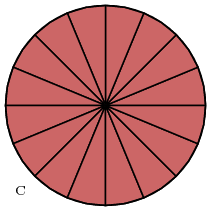
He then cut the polygon into triangles, and “unrolled it” along its perimeter, into a sawtooth of wedges. This unrolling has not changed the total area, so this line of triangles has the same area as the original polygon.

Then, Archimedes recalls that the area of a triangle is given by half its base times its height: that means if you shear a triangle, the area is unchanged as both the base and height are not altered by the procedure.

So, Archimedes shears all of the triangles along the sawtooth to the left, until all of their vertices coincide atop the perpendicular to the leftmost edge.

Thus, for every regular
It is important one does not come away with the impression that it must just ‘obviously’ work, and that once Archimedes had his argument for polygons he was essentially done. Perhaps the best way to see this is to consider for yourself a seemingly analogous argument, which completely fails.
Exercise 4.1 (Convergence to the Diagonal) Consider a simpler analog of Archimedes’ situation, where instead of trying to measure a curve using straight lines, we are trying to measure a straight diagonal line using only horizontal and vertical segments. The following sequence of paths converges pointwise to the diagonal of the square, but what happens to the lengths?

If you believed that because this sequence of curves limits to the diagonal, its sequence of lengths must limit to the length of the diagonal, what would you have conjectured the pythagorean theorem to be?
To compute the convergence of areas, Archimedes was able to make clever use of the already existing area axioms (of Euclid’s common notions, our Definition 3.1). However, to measure the length of a curved segment, Archimedes had to introduce two new axioms (as the measurement of curves is not possible in Euclid’s framework).
Definition 4.1 (Archimedes Axiom I) If

Definition 4.2 (Archimedes Axiom II) If there are two convex paths from

Archimedes could not prove these axioms, as there was no deeper fundamental theory of lengths to rely on. However by formulating his argument axiomatically, he located any possible uncertainty in the axioms themselves: if these two plausible statements were true, then his striking conclusion necessarily followed.
Like much of Archimedes’ work, these axioms were incredibly prescient and hit on deep truths of mathematics. In our modern re-building of geometry we will in fact take Archimedes’ axiom 1 as the definition of a straight line. And Archimedes’ restriction to only considering convex curves was also essential: we’ve already seen in Exercise 8 how delicate arguments can be. But it’s even worse than this: when you drop the convexity requirement its not even true anymore that all curves must have a length (see the bit at the end of this section for an example).
The surviving text of Measurement of the Circle is only fragmentary, but if you wish to read some of the argument in its original (translated) form you can find it here.
Should you open this text you may be at first shocked by the quantity of numbers you see - in Greek works usually geometry reigns supreme and there is essentially no algebra to be found. But here Archimedes takes the opportunity to deduce a practical consequence from the theoretical development discussed above.
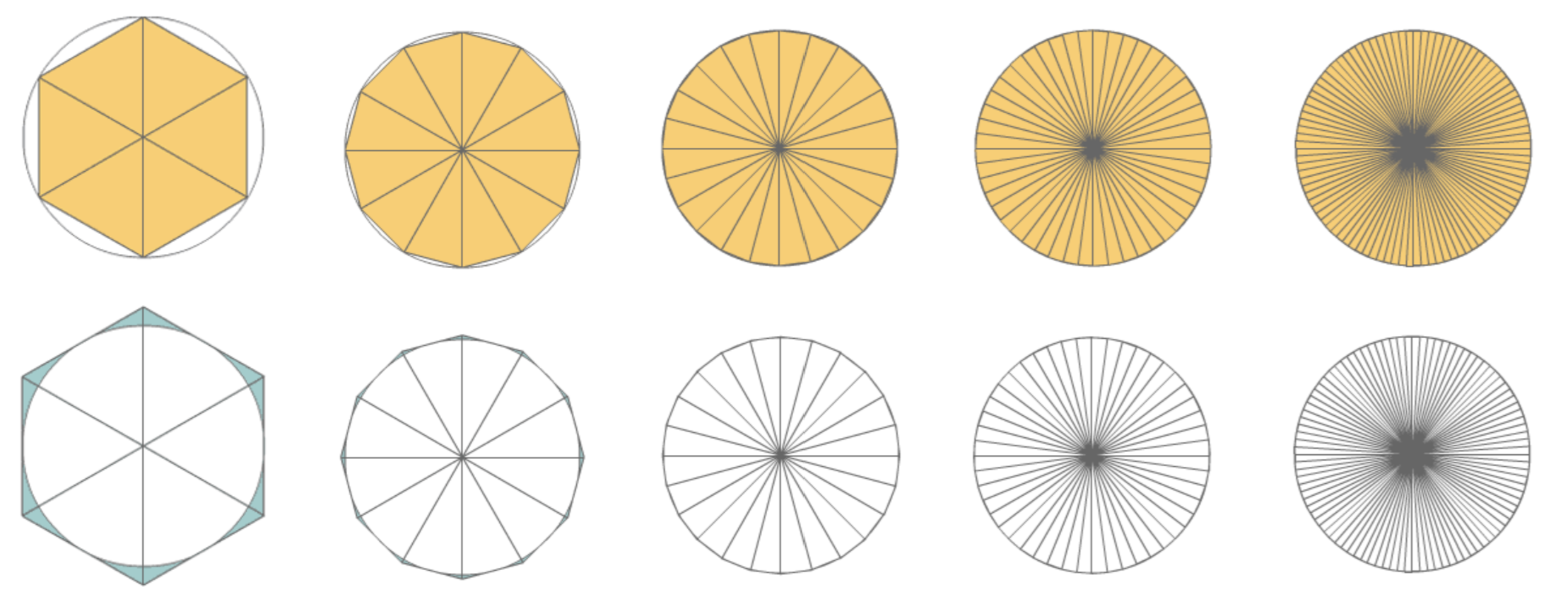
| Sides | Inscribed | Circumscribed |
|---|---|---|
| 6 | 3.0 | 3.4641 |
| 12 | 3.1058 | 3.2154 |
| 24 | 3.1326 | 3.1597 |
| 48 | 3.1394 | 3.1461 |
| 96 | 3.1410 | 3.1427 |
A Fractal in the Plane
The Koch Snowflake is a fractal, defined as the limit of an infinite process starting from a single equilateral triangle. To go from one level to the next, every line segment of the previous level is divided into thirds, and the middle third replaced with the other two sides of an equilateral triangle built on that side.

Doing this to every line segment quickly turns the triangle into a spiky snowflake like shape, hence the name. Denote by
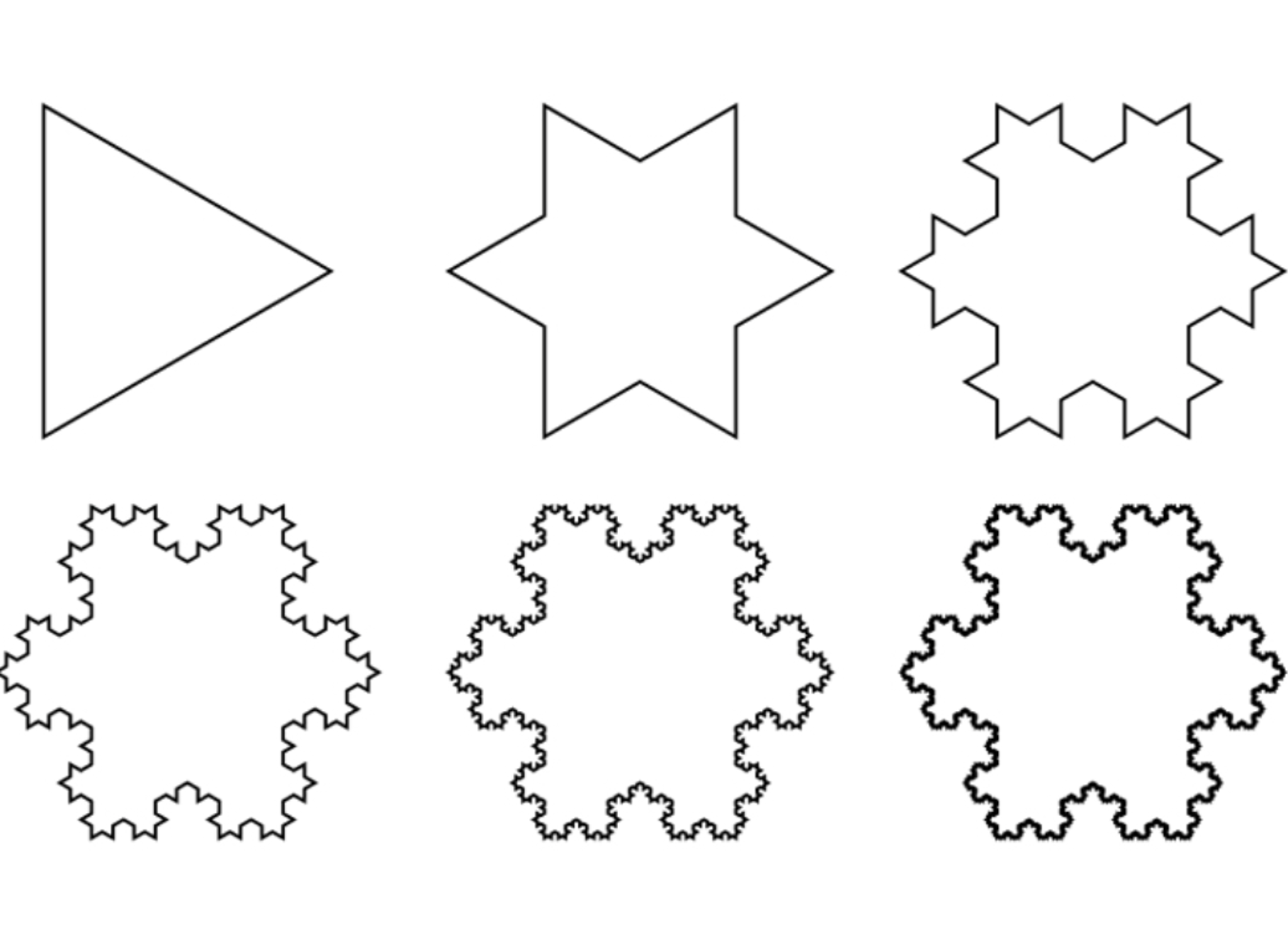
Say the initial triangle at level
Exercise 4.2 (The Koch Snowflake Length) What are the perimeters
Explain why as
Before doing the next problem: ask yourself what happens to the area of an equilateral triangle when you shrink its sides by a factor of 3? Can you draw a diagram (similar to that from last week’s Exercise 2 but larger) to see what the ratio of areas must be?
Exercise 4.3 (The Koch Snowflake Area) What are the areas
Find an infinite series that represents the area of the
4.2 Quadrature of the Parabola
Archimedes also found the area enclosed by a segment of a parabola and a straight line through an ingenious infinite process. His theorem relates the area of this parabolic segment to the area of the largest triangle that can be inscribed within.
Theorem 4.2 The area of the segment bounded by a parabola and a chord is
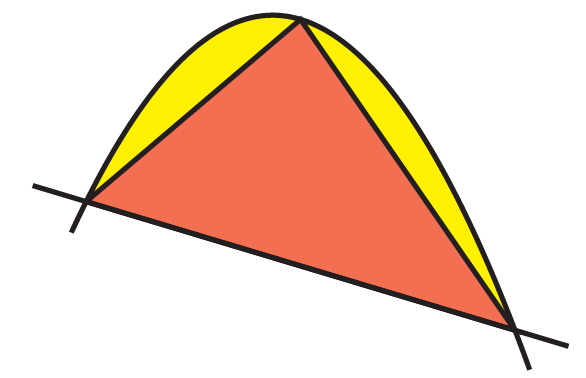
After first describing how to find the largest inscribed triangle (using a calculation of the tangent lines to a parabola), Archimedes notes that this triangle divides the remaining region into two more parabolic regions. And, he could fill these with their largest triangles as well!
These two triangles then divide the remaining region of the parabola into four new parabolic regions, each of which has their own largest triangle, and so on.
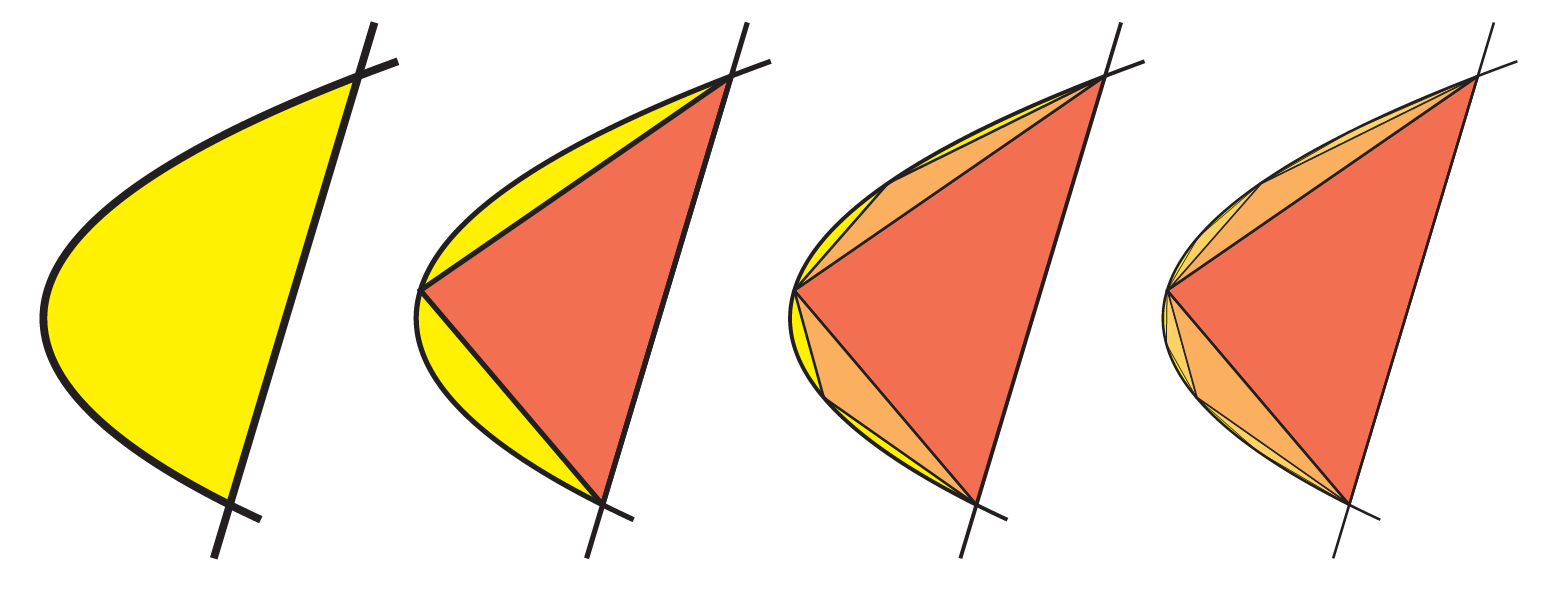
Archimedes proves that in the limit, after doing this infinitely many times, the triangles completely fill the parabolic segment, with zero area left over. Thus, the only task remaining is to add up the area of these infinitely many triangles. And here, he discovers an interesting pattern.
We will call the first triangle in the construction stage 0 of the process. Then the two triangles we make next comprise stage 1, the ensuing four triangles stage 2, and the next eight stage 3.
Proposition 4.1 (Area of the
If
And the total area
Now Archimedes only has to sum this series. For us moderns this is no trouble: we recognize this immediately as a geometric series
But why is it called geometric? Well (this is not the only reason, but…) Archimedes was the first human to sum such a series, and he did so completely geometrically. Ignoring the leading



He then notes that this is precisely one third the area of the bounding square, as two more identical copies of this sequence of squares fill it entirely (just slide our squares to the left, or down). Thus, this infinite sum is precisely

Exercise 4.4 Use the result of Exercise 2 (that you can inscribe an equilateral triangle with half the side lengths) to produce an alternative proof of Archimedes sum, but dividing up a triangle instead of a square.
Exercise 4.5 Construct an argument in the same spirit as archimedes to show the following equality:
4.3 The Sphere and the Cylinder
Archimedes continued his investigations of curves into the third dimension, where he proved fundamental results about the sphere.
Theorem 4.3 (Sphere Volume: Archimedes) The volume of the sphere is equal to the volume of its enclosing cylinder, minus the right circular cone with the same base and height.
That is, the sphere’s volume is
Like before, Archimedes required careful use of the method of exhaustion to prove that equality held in the limit. Modern calculus allows us to reach the same result directly from Archimedes’ insight much faster.
Exercise 4.6 (Sphere and Cone Slices) Using Calculus, find the volume of both of these shapes as volumes of revolution and show they are equal.
But Archimedes was not content to understand the volume of the sphere, he also wanted to relate its surface area to the area of a known shape. He succeeded via an absolutely ingenious argument, to prove the following
Theorem 4.4 (Sphere Surface Area: Archimedes) The surface area of a sphere is equal to that of its enclosing cylinder.
Mathematics yutuber 3Blue1Brown has made an excellent video discussing Archimedes proof, which I encourage you to watch: we would have a movie day in class if I we did not have many other interesting places to go!
Archimedes himself was so proud of this argument that he instructed that a sphere and cylinder be engraved on his tombstone. After he was killed during the Roman invasion of Syracruse in 212BCE, his tomb was quickly forgotten, only to be found centuries later when the great roman orator Cicero searched it out in 75BCE. In his own words:
“Once, while I was superintendent in Syracuse, I brought out from the dust Archimedes, a distinguished citizen of that city. In fact, I searched for his tomb, ignored by the Syracusans, surrounded on all sides and covered with brambles and weeds. The Syracusan denied absolutely that it existed, but I possessed the senari verses written on his tomb, according to which on top of the tomb of Archimedes a sphere with a cylinder had been placed. But I was examining everything with the eyes … And shortly after I noticed a small hill not far emerged from the bushes. On it there was the figure of a sphere and a cylinder. And I said immediately to the Syracusans “That’s what I wanted!” > Cicero, 75 BC
If you are interested in reading Archimedes’ original work a translation of the paper The Sphere and the Cylinder is available here.